统计学 第五章 概率基础 480060000 口东部 西部 口北部 0 第一季度 第二季度 第三季度 第四季度
第五章 概率基础 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 第一季度 第二季度 第三季度 第四季度 东 部 西 部 北 部

本章主要内容 统计学 概率论的发展史 随机事件(Random Events) ■概率的统计定义 m古典概型(Classical Probability) m几何概率(Geometric Probability) 条件概率(Conditional Probabi lity) 事件的独立性(Independence of Events)
本章主要内容 ◼ 概率论的发展史 ◼ 随机事件(Random Events) ◼ 概率的统计定义 ◼ 古典概型(Classical Probability) ◼ 几何概率(Geometric Probability) ◼ 条件概率(Conditional Probability) ◼ 事件的独立性(Independence of Events)

第一节 随机事件 统计学 随机试验(Random exper iment) 为研究随机现象规律性,往往进行试验。例如: 1.抛一枚硬币,观察正面、反面出现的情况。 2.将一枚硬币抛三次,观察出现正面的次数。 3.抛一枚骰子,观察出现的点数。 4.记录车站售票处一天内售出的车票数。 5.在一批灯泡中任意抽取一只,测试它的寿命。 6.记录某地一昼夜的最高温度和最低温度
第一节 随机事件 一、随机试验(Random experiment) 为研究随机现象规律性,往往进行试验。例如: 1. 抛一枚硬币,观察正面、反面出现的情况。 2. 将一枚硬币抛三次,观察出现正面的次数。 3. 抛一枚骰子,观察出现的点数。 4. 记录车站售票处一天内售出的车票数。 5. 在一批灯泡中任意抽取一只,测试它的寿命。 6. 记录某地一昼夜的最高温度和最低温度

统计学 这些试验都具有以下的特点: 可重复性:可在相同条件下重复进行 可预知性:试验可能结果不止一个,但能确定所有 的可能结果结果不止一个,并且能事先明确试验的 所有可能结果; 随机性:一次试验之前无法确定具体是哪种结果 出现。 在概率论中,我们将具有上述三个特点的试验称 为随机试验(Random exper iment),表示为E 0
这些试验都具有以下的特点: ◼ 可重复性:可在相同条件下重复进行 ◼ 可预知性:试验可能结果不止一个,但能确定 所有 的可能结果结果不止一个,并且能事先明确试验的 所有可能结果; ◼ 随机性:一次试验之前无法确定具体是哪种 结果 出现。 在概率论中,我们将具有上述三个特点的试验称 为随机试验(Random experiment),表示为E

二、事件(Event) 统计学 00 必然事件2:某件事情在一次试验中一定发生 如:“在一副扑克牌中任摸14张,其中有两张花色是不同” 就是必然事件。 不可能事件☑:某件事情在一次试验中一定不发生 如:“在一副扑克牌中任摸14张,其中没有两张花色是不同的” 就是不可能事件。 随机事件(A,B,C,.):某件事情在一次试验中既可 能发生,也可能不发生 如:“掷一枚硬币,出现正面朝上” “扔一枚骰子,出想6点
二、事件(Event) ◼ 必然事件 :某件事情在一次试验中一定发生 如: “在一副扑克牌中任摸14张,其中有两张花色是不同” 就是必然事件。 ◼ 不可能事件 :某件事情在一次试验中一定不发生 如:“在一副扑克牌中任摸14张,其中没有两张花色是不同的” 就是不可能事件。 ◼ 随机事件(A,B,C,.) :某件事情在一次试验中既可 能发生,也可能不发生 如:“掷一枚硬币,出现正面朝上” “扔一枚骰子,出想6点”

统计学 基本事件(0,0,):试验的每一个结果都是一个事件,这 些事件不可能再分解成更简单的事件 一般的事件由基本事件复合而成。 例如:考察掷一个骰子一次的试验,可能发生的结果有6种 ·“掷得1点” ·“掷得2点” ·“掷得3点” ·“掷得4点” ·“掷得5点” 基本事件 ·“掷得6点号 “掷得奇数1 “掷得偶数 复合事件
•基本事件( ):试验的每一个结果都是一个事件,这 些事件不可能再分解成更简单的事件 •一般的事件由基本事件复合而成。 例如:考察掷一个骰子一次的试验,可能发生的结果有6种 • “掷得1点” • “掷得2点” • “掷得3点” • “掷得4点” • “掷得5点” • “掷得6点” • “掷得奇数” • “掷得偶数” 基本事件 复合事件 0 1 ,

统计学 例1对于试验E:将一枚硬币连抛三次,考虑正 反面出现的情况,若记“正面”为H, “反面” 为T, 则基本事件有:HHH,HHT,HTH,THH,HTT, THT,TTH,TTT 随机事件 A=“至少出一个正面” =HHH,HHT,HTH,THH,HTT,THT,TTH; B=“两次出现同一面”三HHH,TTT C=“恰好出现一次正面”=HTT,THT,TTH母
例1 对于试验E: 将一枚硬币连抛三次,考虑正 反面出现的情况,若记“正面”为H, “反面” 为T, 则基本事件有:HHH, HHT, HTH, THH,HTT, THT,TTH , TTT 随机事件 A=“至少出一个正面” ={HHH, HHT, HTH, THH,HTT,THT,TTH}; B=“两次出现同一面”={HHH,TTT} C=“恰好出现一次正面”={HTT,THT,TTH}

三、事件的集合论定义 统计学 20世纪,冯.米泽斯(Von Mises)开始用集合论研究事件。 1.样本空间 。样本点:随机试验E的每一个可能结果 样本空间:样本点的全体,即随机试验的所有可能结果组 成的集合,记为 例1:掷一枚硬币,考察出现向上的面,试验的可能结果有: “正面向上”,“反面向上”两个,则样本空间为: 2={“正面向上”,“反面向上”} 若采用记号0一“正面向上”,o,=“反面向上 则2={0,02}
◼ 20世纪,冯.米泽斯(Von Mises)开始用集合论研究事件。 1. 样本空间 ◼ 样本点:随机试验E的每一个可能结果 ◼ 样本空间:样本点的全体,即随机试验E的所有可能结果组 成的集合,记为 。 ◼ 例1:掷一枚硬币,考察出现向上的面,试验的可能结果有: “正面向上” , “反面向上”两个,则样本空间为: 三、事件的集合论定义 1 2 2 1 若采用记号 =“正面向上” , =“反面向上” 则 = , =“正面向上” , “反面向上”

统计学 2.事件的集合论定义 000000●■000000■000 事件可以看作是样本空间的子集 符号 集合论解释 概率论解释 2 空间 必然事件、样本空间 空集 不可能事件 ) 点(元素) 基本事件、样本点 A 子集A 事件A 0∈A O是A中的点 事件A发生 0庄A ①不是A中的点 事件A不发生
2. 事件的集合论定义 ◼ 事件可以看作是样本空间的子集 不是A中的点 事件A不发生 是A中的点 事件A发生 A 子集A 事件A 点(元素) 基本事件、样本点 空集 不可能事件 空间 必然事件、样本空间 符号 集合论解释 概率论解释 A A
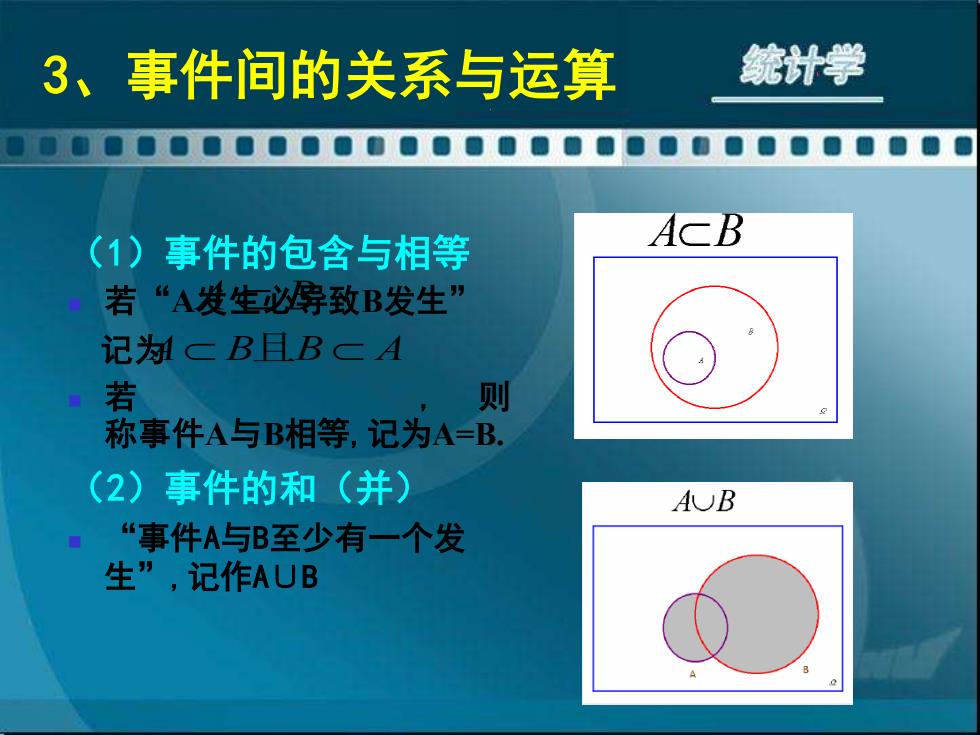
3、事件间的关系与运算 统计学 (1)事件的包含与相等 ACB 若“A发生必碑致B发生” 记为湖三B目B三A 若 则 称事件A与B相等,记为A=B. (2)事件的和(并) AUB “事件A与B至少有一个发 生”,记作AUB
(1)事件的包含与相等 ◼ 若“A发生必导致B发生” 记为 ◼ 若 , 则 称事件A与B相等,记为A=B. (2)事件的和(并) ◼ “事件A与B至少有一个发 生” ,记作A∪B 3、事件间的关系与运算 A B A B B A 且