
第6章总体率的区间估计和假设检验目录 第一节率的抽样误差与区间估计 第二节率的检验 第三节卡方检验 ☐第四节四格表确切概率法 简历 返回总目绿 返回章目录4口>]口结束幻 第6章总体率的区间估计和假设检验 第5页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第5页 第6章 总体率的区间估计和假设检验 目录 ❑ 第二节 率的u检验 ❑ 第三节 卡方检验 ❑ 第四节 四格表确切概率法 ❑ 第一节 率的抽样误差与区间估计

第六章学习要求 1. 掌握:率的抽样误差的概念及意义。 2. 熟悉:总体率的区间估计的概念、意义及其计算方法。 3. 掌握:率的u检验的概念、意义。 4. 熟悉:率的u检验的适用条件及计算方法。 5. 掌握:卡方检验的概念及意义;检验的分类、适用条 件及计算方法。 6. 熟悉:行列表卡方检验的适用条件及计算方法。 7. 了解:行列表卡方检验的注意事项及行列表分割法 了解:四格表确切概率法应用条件。 筒历 返回总目录返回章目录口>]口结束 第6章总体率的区间估计和假设检验 第6页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第6页 1. 掌握:率的抽样误差的概念及意义。 2. 熟悉:总体率的区间估计的概念、意义及其计算方法。 3. 掌握:率的u检验的概念、意义。 4. 熟悉:率的u检验的适用条件及计算方法。 5. 掌握:卡方检验的概念及意义;检验的分类、适用条 件及计算方法。 6. 熟悉:行列表卡方检验的适用条件及计算方法。 7. 了解:行列表卡方检验的注意事项及行列表分割法 8. 了解:四格表确切概率法应用条件。 第六章 学习要求

第一节 率的抽样误差与总体率的区间估计(1)》 一、率的抽样误差 1. 率的抽样误差:在同一总体中按一定的样本含 量抽样,样本率和总体率或样本率之间也存在 着差异,这种差异称为率的抽样误差。 2.率的抽样误差的大小是用率的标准误来表示的。 π(1-π) p(1-p) n 简历 返回总目绿」 返回章录口>】口结束 第6章总体率的区间估计和假设检验 第7页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第7页 1. 率的抽样误差:在同一总体中按一定的样本含 量n抽样,样本率和总体率或样本率之间也存在 着差异,这种差异称为率的抽样误差。 2. 率的抽样误差的大小是用率的标准误来表示的。 n p (1 ) − = n p p S p (1− ) = 第一节 率的抽样误差与总体率的区间估计(1) 一、率的抽样误差:

For example 1.例6.1检查居民800人粪便中蛔虫阳性200人, 阳性率为25%,试求阳性率的标准误。 2.本例:n=800,p=0.25,1-p=0.75, 0.25×0.75 0.0153=1.53% 800 筒历 返回总目录 返回章目录]口>口结束 第6章总体率的区间估计和假设检验 第8页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第8页 For example 1. 例6.1 检查居民800人粪便中蛔虫阳性200人, 阳性率为25%,试求阳性率的标准误。 2. 本例:n=800,p=0.25,1-p=0.75, 0.0153 1.53% 800 0.25 0.75 = = S p =

二、总体率的区间估计 1.总体率的区间估计 (正态分布法 样本含量n足够大,np与n(1-p)均≥5时, 筒历 返回总目绿 返回章目录4口>]口结束幻 第6章总体率的区间估计和假设检验 第9页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第9页 1. 总体率的区间估计 ㈠正态分布法 样本含量n足够大, np与n(1-p)均≥5时 , p u Sp 二、总体率的区间估计

表(补充) np与n(1-p)均≥5时 样本含量大小估计 表6-a 不同的p所对应的至少的样本含呈n n pxn 至少25 10 0.5×10 =5.0 13 0.4×13 =5.2 17 0.3×17 =5.1 25 0.2×25 =5.0 50 0.1×50 =5.0 500 0.01×500 =5.0 筒历 返回总目录 返回章目录]口>口结束 第6章总体率的区间估计和假设检验 第10页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第10页 表(补充) np与n(1-p)均≥5时 样本含量大小估计

For example 1.例6.2求例6.1当地居民粪便蛔虫阳性率的 95%可信区间和99%的可信区间。 2.95%的可信区间为:25%±1.96×1.53% 即(22.00%,28.00%) 3.99%的可信区间为:25%±2.58×1.53% 即(21.05%,28.95%) 简历 返回总目绿 返回章目录4口>]口结束幻 第6章总体率的区间估计和假设检验 第11页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第11页 For example 1. 例6.2 求例6.1当地居民粪便蛔虫阳性率的 95%可信区间和99%的可信区间。 2. 95%的可信区间为:25%±1.96×1.53% 即(22.00%,28.00%) 3. 99%的可信区间为:25%±2.58×1.53% 即(21.05%,28.95%)

(二)查表法 1.当样本含量较小(如ns50),np或n(1 p)]口结束 第6章总体率的区间估计和假设检验 第12页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第12页 1. 当样本含量较小(如n≤50),np或n(1- p)<5时,样本率的分布呈二项分布,总体率 的可信区间可据二项分布的理论求得。 2. 例6.3 某医院用某药治疗脑动脉硬化症22例, 其中显效者10例。问该药总显效率的95%可 信区间为多少? 3. 本例n=22, X=10, 查附表7(201页),得 此两数相交处的数值为24~68,即该药总显 效率的95%可信区间为(24%,68%)。 (二)查表法

第二节率的u检验 1.应用条件:样本含量n足够大,np与 n(1-p)均≥5。见补充表6a。 2.此时,样本率p也是以总体率为中心呈 正态分布或近似以正态分布。 简历 返回总目录 返回章耳录(幻4口>]口结束 第6章总体率的区间估计和假设检验 第13页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第13页 第二节 率的u检验 1. 应用条件:样本含量n足够大, np与 n(1-p)均≥5 。见补充表6a。 2. 此时,样本率p也是以总体率为中心呈 正态分布或近似正态分布
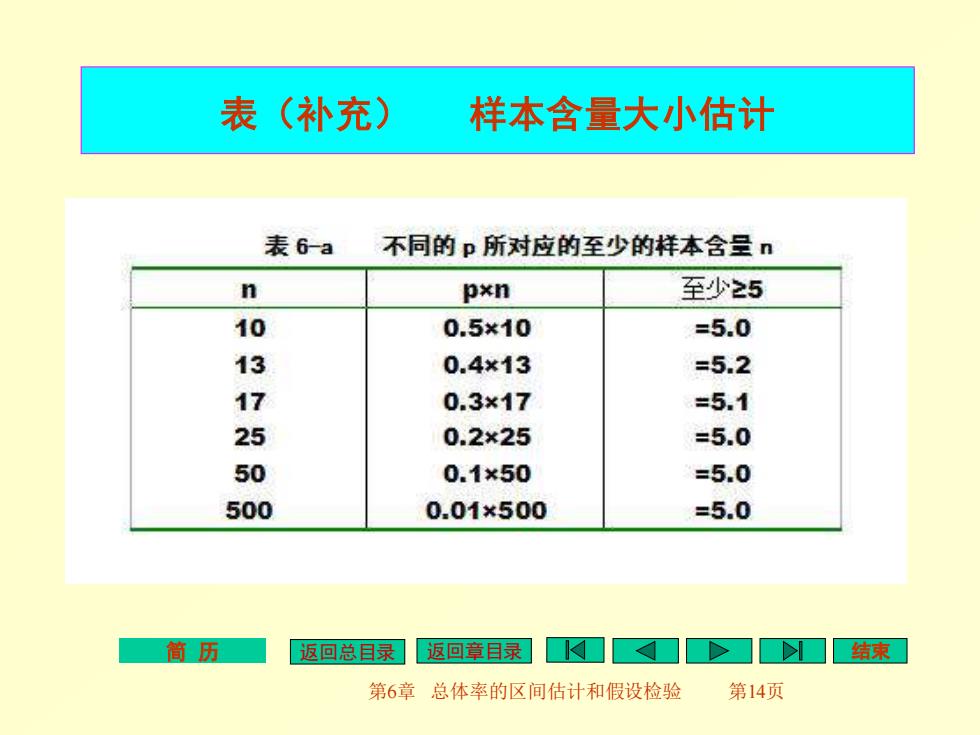
表(补充》 样本含量大小估计 表6-a 不同的p所对应的至少的样本含呈n n pxn 至少25 10 0.5×10 =5.0 13 0.4×13 =5.2 17 0.3×17 =5.1 25 0.2×25 =5.0 50 0.1×50 =5.0 500 0.01×500 =5.0 筒历 返回总目录 返回章目录]口>口结束 第6章总体率的区间估计和假设检验 第14页
简 历 返回总目录 返回章目录 结束 第6章 总体率的区间估计和假设检验 第14页 表(补充) 样本含量大小估计