
统计学 第六章 抽样分布
第六章 抽样分布

本章主要内容 统计学 §6.1 三种不同性质的分布 §6.2 一个总体参数推断时样本统计量分布 §6.3 两个总体参数推断时样本统计量分布
本章主要内容 §6.1 三种不同性质的分布 §6.2 一个总体参数推断时样本统计量分布 §6.3 两个总体参数推断时样本统计量分布

第一节三种不同性质的分布 统计学 总体分布 样本分布 抽样分布
第一节 三种不同性质的分布 一. 总体分布 二. 样本分布 三. 抽样分布

、 总体分布 统计学 1.总体中各元素的观察值所形成的分布 2.分布通常是未知的 3.可以假定它服从某种分布
1. 总体中各元素的观察值所形成的分布 2. 分布通常是未知的 3. 可以假定它服从某种分布 一、总体分布 总体

二、样本分布 统计学 1.一个样本中各观察值的分布 2.也称经验分布 3.当样本容量n逐渐增大时,样本分布逐渐 接近总体的分布
1. 一个样本中各观察值的分布 2. 也称经验分布 3. 当样本容量n逐渐增大时,样本分布逐渐 接近总体的分布 二、样本分布

三、抽样分布 统计学 1.样本统计量的概率分布 2.例如:样本均值,样本比例,样本方差等 3.提供了来自总体的一部分信息,是进行推 断的理论基础
1. 样本统计量的概率分布 2. 例如:样本均值, 样本比例,样本方差等 3. 提供了来自总体的一部分信息,是进行推 断的理论基础 三、抽样分布
三、抽样分布 统计学 样本均值 0 样本方差 样本 抽样分布 总体
三、抽样分布 抽样分布 总 体 样 本 样本方差 样本均值

第二节单总体样本统计量的抽样分布 统计学 082ag 样本均值的抽样分布 样本比例的抽样分布 三 抽样方差的抽样分布
第二节 单总体样本统计量的抽样分布 一. 样本均值的抽样分布 二. 样本比例的抽样分布 三. 抽样方差的抽样分布

一、样本均值的抽样分布 统计学 1. 容量相同的所有可能样本的样本均值的概率 分布 2.是进行推断总体总体均值u的理论基础
一、样本均值的抽样分布 1. 容量相同的所有可能样本的样本均值的概率 分布 2. 是进行推断总体总体均值的理论基础
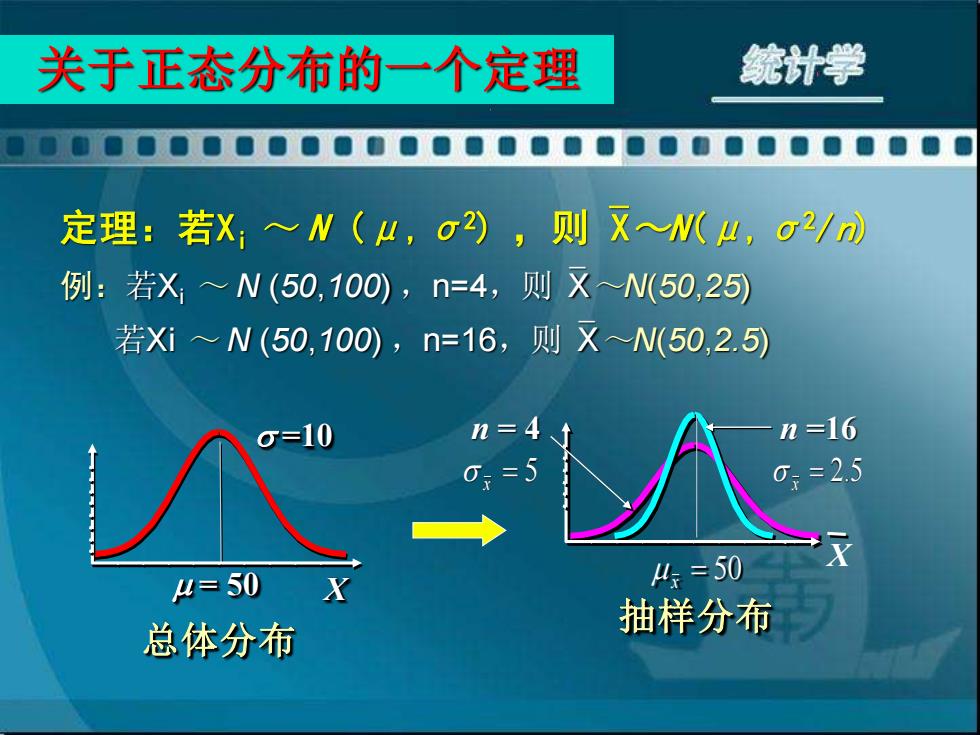
关于正态分布的一个定理 统计学 定理:若X≈W(μ,o),则XW4,g2/) 例:若X~N(50,100),n=4,则X~N50,25) 若Xi>N(50,100),n=16,则XN(50,2.5) g=10 n=4 n=16 0=5 0=25 4=50 X 4=50 总体分布 抽样分布
关于正态分布的一个定理 = 50 =10 X 总体分布 n = 4 抽样分布 X n =16 = 5 x = 50 x = 2.5 x 定理:若Xi ~ N (μ,σ2) ,则X~N(μ,σ2/n) 例:若Xi ~ N (50,100) ,n=4,则X~N(50,25) 若Xi ~ N (50,100) ,n=16,则X~N(50,2.5)