
第五章拉普拉斯变换 ·§5.1定义、存在性 ● §5.2性质 §5.3拉普拉斯逆变换 §5.4系统函数 §5.5线性定常系统频率响应 ·§5.6B1B0稳定性 ·§5.7全通系统/最小相移系统 2
2 第五章 拉普拉斯变换 • §5.1 定义、存在性 • §5.2 性质 • §5.3 拉普拉斯逆变换 • §5.4 系统函数 • §5.5 线性定常系统频率响应 • §5.6 BIBO稳定性 • §5.7 全通系统/最小相移系统

§5.1定义、存在性 ·信号f(t)的傅里叶变换存在要求: f(t)∈L[-oo,+oo],但sgn(t)EL, F {sgn(t))=lim Feof(t)>0. 考虑是否可以将o纳入积分核? ·对因果信号f(t)=f(t)u(t), F ea()f(t)emJemdif(t)edi =0f()e“dt=L{f()} 3
3 §5.1 定义、存在性 • 信号f (t)的傅里叶变换存在要求: 考虑是否可以将 纳入积分核? • 1 1 0 L , , sgn L , sgn lim , 0 t f t t t e f t F F 但 。 t e -j j 0 0 0 , d d d t t t t st f t f t u t e f t f t e e t f t e t f t e t f t F L 对因果信号

§5.1定义、存在性 ·定义信号f(t)的(单边)拉普拉斯变换为 F(s)门L{f()}DDf()e“dt,s=o+jo f(t)e(t)ewdrd 令s=o+jo,o为常数,ds=jd0 f0=2r(o)es f07L{(加2Fo)eas 4
4 §5.1 定义、存在性 • 定义信号f (t)的(单边)拉普拉斯变换为 0 j j 0 j j j j 1 j d , j 1 d d 2 j , d jd 1 d 2 j 1 d 2 j st t t t t s t F s f t f t e t s f t e f t e t e s s f t F s e s f t F s F s e s L L 令 为常数

§5.1定义、存在性 ● 定义(指数阶函数):指f(t)分段连续(存 在有限个第一类间断点),且3M>0,T>0, 使f(t)≤Me,对∀t>T。 注:f(t)=0(e) ·F(s)存在:F(s)<o。 ·命题:指数阶信号的拉式变换存在。 5
5 §5.1 定义、存在性 • 定义(指数阶函数):指f (t)分段连续(存 在有限个第一类间断点),且 注: • • 命题:指数阶信号的拉式变换存在。 M T 0, 0, 0 , t f t Me t T 使 对 。 O 0 t f t e F s F s 存在:
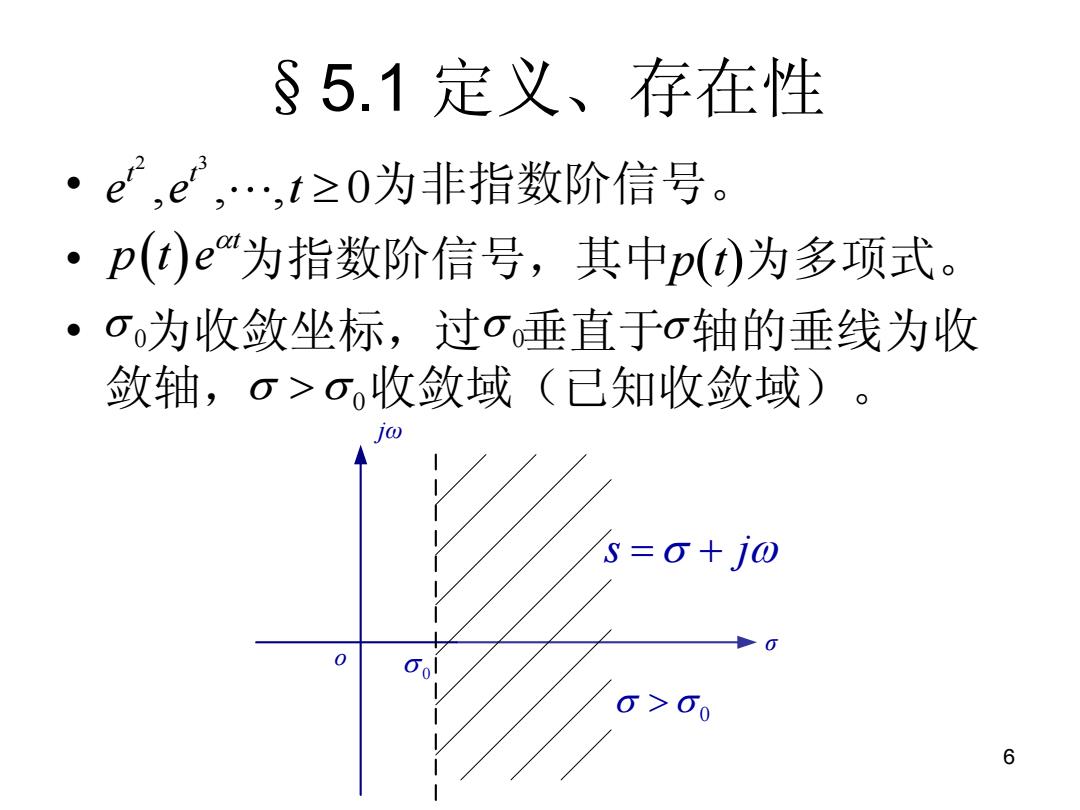
§5.1定义、存在性 e,e,…,t≥0为非指数阶信号。 ·p(t)e"为指数阶信号,其中p()为多项式。 。( 为收敛坐标,过o垂直于σ轴的垂线为收 敛轴,o>σ收敛域(已知收敛域)。 10 S=0+j10 O> 6
6 §5.1 定义、存在性 • 为非指数阶信号。 • 为指数阶信号,其中p(t)为多项式。 • 为收敛坐标,过 垂直于 轴的垂线为收 敛轴, 收敛域(已知收敛域)。 2 3 , , , 0 t t e e t t p t e 0 0 0 σ o jω 0 0 s j

§5.1定义、存在性 ·例:f(t)=u(t) u(t)≤1e",M=1,T=0,o。=0,o>0收敛 好-c- 6>01 S ·例: L fe)ee 0>-Q 1 a+s a+s 7
7 §5.1 定义、存在性 • 例: • 例: 0 0 0 0 0 1 , 1, 0, 0, 0 1 d | t st st f t u t u t e M T e u t e t s s L 收敛 0 0 1 d | s t t t st e e e e t s s L

§5.1定义、存在性 ·例:L{r}=ed-0L{-} Laoy-日 L{eey- 1 Lrao-g ! 8
8 §5.1 定义、存在性 • 例: 1 0 2 1 d 1 1 ! n n st n n n n t t e t t s u t s tu t s n t u t s L L L L L

§5.1定义、存在性 ·积分下限:当f(t)在t=0处第一类间断, F(s)=L{f()}=0f()e“dt =∫f()e"dt =0f()e"d -注:∫'(t)o~δ(),”(t)儿o~8(t),解微分方程 的初(边)值问题。 9
9 §5.1 定义、存在性 • 积分下限:当 f (t)在t = 0处第一类间断, – 注: ,解微分方程 的初(边)值问题。 0 0 0 d d d st st st F s f t f t e t f t e t f t e t L f t t f t t | ~ , | ~ t t 0 0

§5.2性质 ·1.代数性质 -能性:L位a0-立aL -卷积:L{f()*()}=F(s)F(s) 零状态响应 f h(@=方(@) (t) →f()*f()=y() ① ① F(S) 0 F(S(S) H()=Lh(=F(S) 10
10 §5.2 性质 • 1. 代数性质 – 线性: – 卷积: 1 1 n n i i i i i i f t f t L L L f t f t F s F s 1 2 1 2 1 1 f t F S 1 2 1 2 f t f t y t F S F S 2 2 h t f t H h t F S L 零状态响应

§5.2性质 -像卷积(s域卷积): L(00}25(s5(间 =2g-e f() 乘 +f(t)f2(t) 2(t) 11
11 §5.2 性质 – 像卷积(s域卷积): 1 2 1 2 + j 1 2 - j 1 2 j 1 d 2 j f t f t F s F s F z F s z z L 乘 f t 2 f t 1 f t f t 1 2