
第八章Z变换 ·§8.1定义、收敛域 ● §8.2Z变换计算方法 §8.3Z变换性质 §8.4Z变换性质与L变换的关系 §8.5Z变换解差分方程 ·§8.6系统函数、BIBO稳定 2
2 第八章 Z变换 • §8.1 定义、收敛域 • §8.2 Z变换计算方法 • §8.3 Z变换性质 • §8.4 Z变换性质与 L 变换的关系 • §8.5 Z变换解差分方程 • §8.6 系统函数、BIBO稳定

§8.1定义、收敛域 。1.定义:Z变换 -序列x(n)的双边Z变换: X(a)加Z{x(n)}☐∑x(n)z” -序列x(n)的单边Z变换: X(2)加Z{x(n)}D∑x(n)z” n=( 3
3 §8.1 定义、收敛域 • 1.定义: Z变换 – 序列 – 序列 n n x n X z x n x n z Z Z 的双边 变换: 0 n n x n X z x n x n z Z Z 的单边 变换:

§8.1定义、收敛域 -(1)双边:X(e))=2x(m)”=∑x(n)z"+∑x(m)z” 为Laurent级数,其中,∑x(n)z"是Laurent级数 的正则部,∑x(n)z"是主部。 n=0 jlmZ -(2)Z是复平面 上一点 ReZ -(3)对因果序列:单边Z变换=双边Z变换。 4
4 §8.1 定义、收敛域 – (1)双边: – (2)Z是复平面 上一点 – (3)对因果序列:单边 Z变换=双边 Z变换。 1 0 1 0 Laurent , Laurent n n n n n n n n n n X z x n z x n z x n z x n z x n z 为 级数 其中, 是 级数 的正则部, 是主部。 o ReZ jImZ 注:

§8.1定义、收敛域 ·定义:逆Z变换 -对双边Z变换X(z)=∑x(n)z” 2xe=2a[立:也 三2也 C为包围原点的闭曲线'.上式=x(n) 5
5 §8.1 定义、收敛域 • 定义:逆 Z变换 – 对双边 Z变换 n n X z x n z 1 1 C C 1 C 1 C 1 1 d d 2 j 2 j 1 d 2 j 1 1 , d 2 j 0 , C m m n n m n n m n z X z z z x n z z x n z z m n z z m n x n 为包围原点的闭曲线 上式=

§8.1定义、收敛域 -定义)-2f-xet=2-x阳月 jlmZ Z=reio ReZ -注:(*)的求解:z=re,d=rjed0减者留数定理 6
6 §8.1 定义、收敛域 – 定义: – 注: 1 1 C 1 d 2 j m x n z X z z X z Z o ReZ jImZ r j Z re j d j d j z re z r e 的求解: , 或者留数定理

§8.1定义、收敛域 ·2.收敛域 二(定义:对有界x(.x(a三xs 的Z的集合。 -(2)判别方法: |X(2≤∑x(n)z1,则发散; 柯西方法:p1imo 若p=1,则不定。7
7 §8.1 定义、收敛域 • 2. 收敛域 – (1)定义:对有界 – (2)判别方法: 达兰贝尔方法: 柯西方法: n n x n X z x n z Z 一致 ,使 的 的集合。 , n n n n X z x n z a x n z 令 , 1 lim n n n a a lim n n n a 1, 1, 1, 若 则收敛; 若 则发散; 若 则不定

§8.1定义、收敛域 ·3.序列的分类与收敛域 -(1)右边序列:x(n),n∈{n,∞} X(z)=∑x(n)z n=n p=limx(nz≤limx(m-limx(n口R,圆的外部 jlmZ n1<0,R<z<o0 ReZ n1≥0,R,<2≤0 8
8 §8.1 定义、收敛域 • 3.序列的分类与收敛域 – (1)右边序列: x n n n , , 1 1 1 1 lim lim 1 lim , n n n n n n n n n x n X z x n z x n z x n z z x n R 圆的外部 ReZ jImZ o Rx1 1 1 1 1 0, 0, x x n R z n R z

§8.1定义、收敛域 -(2)左边序列x(n),n∈{-∞,n} X(z)=∑x(n)z"=∑x(-n)z" n=-m p≤limx(-nE0,0<z<R n2≤0,0≤z<R 9
9 §8.1 定义、收敛域 – (2)左边序列 x n n n , , 2 1 2 2 2 2 1 2 2 lim 1 lim , 0,0 0,0 n n n n n n n n n x n x x X z x n z x n z x n z z x n R n z R n z R 圆的内部
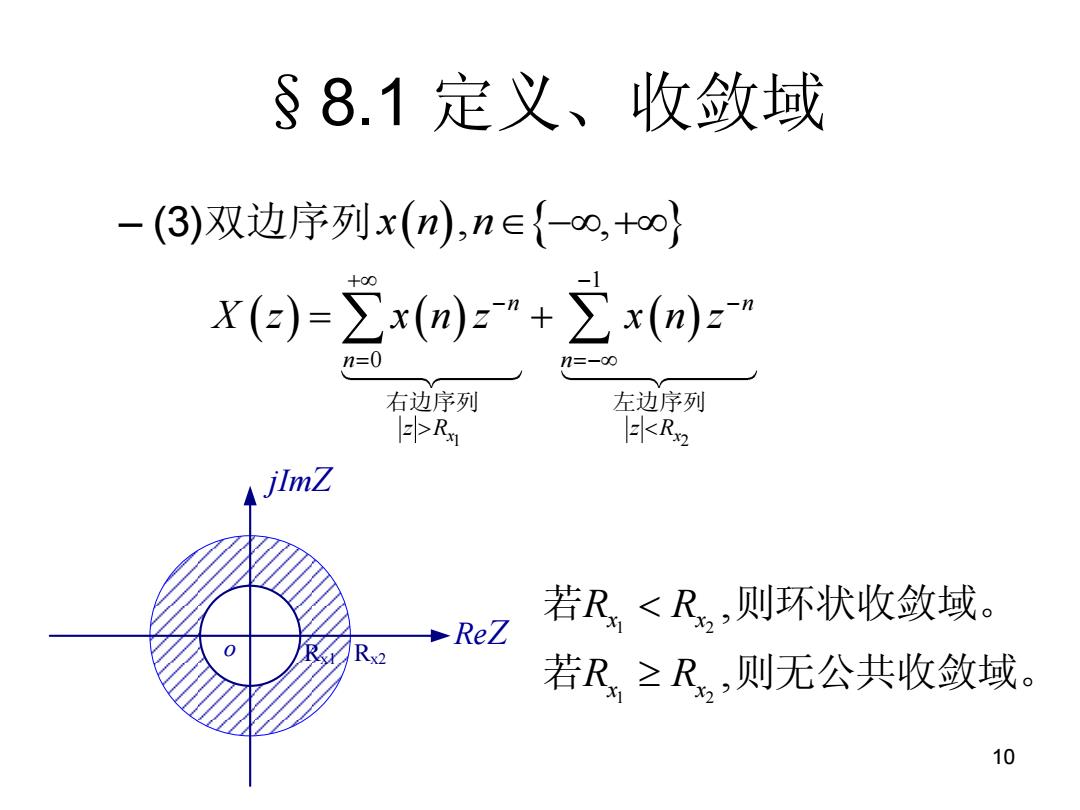
§8.1定义、收敛域 -(3)双边序列x(n),n∈{-∞,+o} X(e)=∑x(n)z"+∑x(n)z” n=0 右边序列 左边序列 Rx KR jlmZ 若R<R,则环状收敛域。 ·ReZ 若R≥R,则无公共收敛域。 10
10 §8.1 定义、收敛域 – (3)双边序列 x n n , , 1 2 1 0 x x n n n n z R z R X z x n z x n z 右边序列 左边序列 ReZ jImZ o Rx1 Rx2 1 2 1 2 , , x x x x R R R R 若 则环状收敛域。 若 则无公共收敛域

§8.1定义、收敛域 ·4.典型序列Z变换 -(1)Z{o(n)}=1,0≤z<o -②za》-立:1ssc (3)fm) =0 11
11 §8.1 定义、收敛域 • 4.典型序列 Z变换 – (1) – (2) – (3) Z n z 1,0 1 0 1 ,1 1 n n u n z z z Z 2 0 ,1 1 n n z nu n nz z z Z