
第一章绪论 ·§1.1信号与系统 ·§1.2信号分类与典型确定性信号 §1.3冲激函数、广义函数 ·§1.4信号分解 0 §1.5系统分类 ·§1.6线性系统 2
2 第一章 绪论 • §1.1 信号与系统 • §1.2 信号分类与典型确定性信号 • §1.3 冲激函数、广义函数 • §1.4 信号分解 • §1.5 系统分类 • §1.6 线性系统
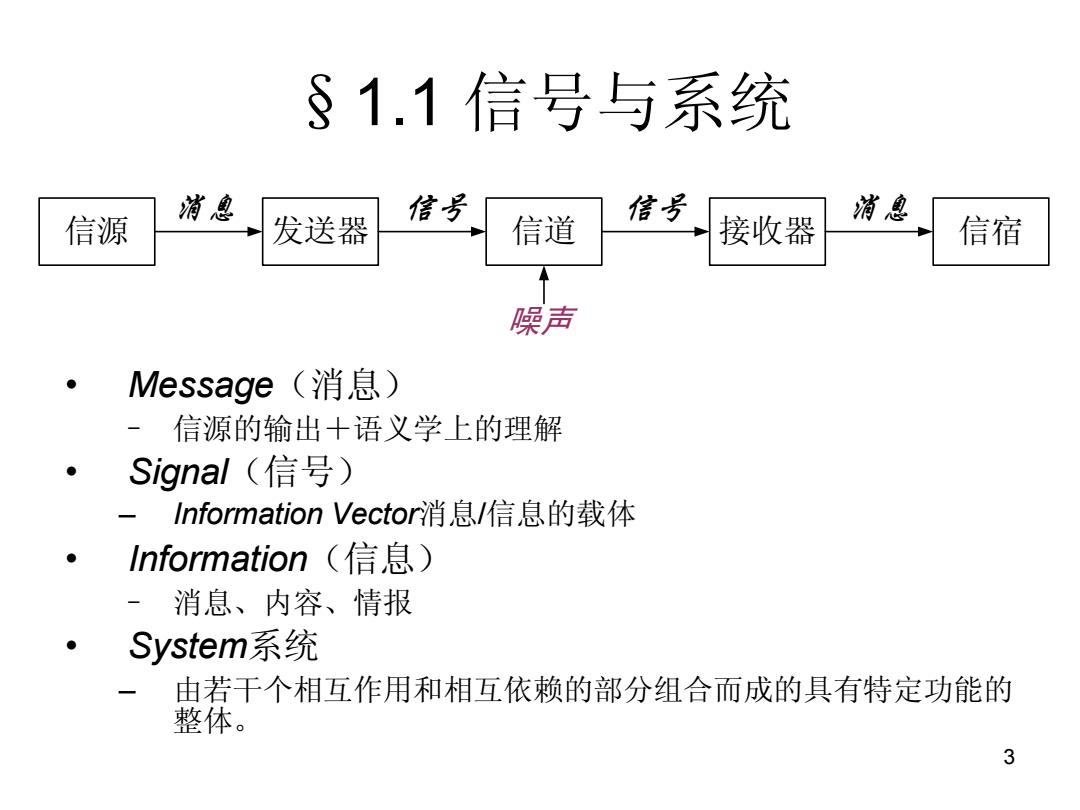
§1.1信号与系统 消息 发送器 信芳 信道 信号 接收器 消息 信源 信宿 噪声 ● Message(消息) 信源的输出十语义学上的理解 ● Signal(信号) -Information Vector消息/信息的载体 Information(信息) 一消息、内容、情报 System系统 由若干个相互作用和相互依赖的部分组合而成的具有特定功能的 整体。 3
3 §1.1 信号与系统 信源 发送器 信道 接收器 信宿 消息 信号 噪声 信号 消息 • Message(消息) – 信源的输出+语义学上的理解 • Signal(信号) – Information Vector消息/信息的载体 • Information(信息) – 消息、内容、情报 • System系统 – 由若干个相互作用和相互依赖的部分组合而成的具有特定功能的 整体

本课要解决的问题 ·信号表示(分析) 一把信号分解成它的各个组成分量或成分的概念、 理论和方法,即用简单表示复杂。 ·信号通过系统 一系统分析 ·在给定系统的条件下,研究系统对于输入激励信号 所产生的输出响应。 一系统综合 。 按某种需要先提出对于给定激励的响应,而后跟据 此要求设计(综合)系统。 4
4 本课要解决的问题 • 信号表示(分析) – 把信号分解成它的各个组成分量或成分的概念、 理论和方法,即用简单表示复杂。 • 信号通过系统 – 系统分析 • 在给定系统的条件下,研究系统对于输入激励信号 所产生的输出响应。 – 系统综合 • 按某种需要先提出对于给定激励的响应,而后跟据 此要求设计(综合)系统

§1.2信号分类与典型确定性信号
§1.2 信号分类与典型确定性信号

信号分类I ·确定性信号 一由确定性系统产生的,物理参数确定的信号。 ·非确定性信号 一随机信号 ·具有不可预知的不确定性的信号。 -模糊信号 6
6 信号分类Ⅰ • 确定性信号 – 由确定性系统产生的,物理参数确定的信号。 • 非确定性信号 – 随机信号 • 具有不可预知的不确定性的信号。 – 模糊信号

信号分类II ·周期信号 -f(t)=f(t+nT),n∈Z ·非周期信号 -f(t)≠f(t+nT),n∈Z 7
7 信号分类Ⅱ • 周期信号 – • 非周期信号 – f t f t nT n , Z f t f t nT n , Z
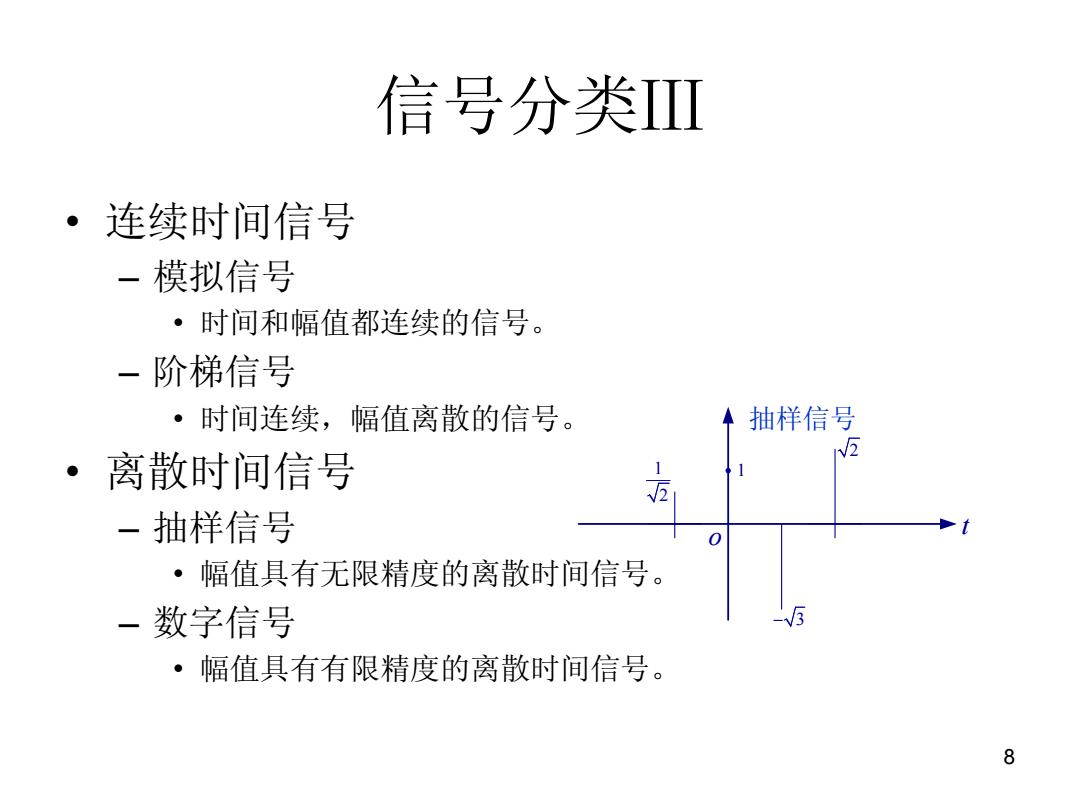
信号分类I ·连续时间信号 一模拟信号 ·时间和幅值都连续的信号。 一阶梯信号 ·时间连续,幅值离散的信号。 ◆抽样信号 5 ·离散时间信号 抽样信号 ·幅值具有无限精度的离散时间信号。 一数字信号 ·幅值具有有限精度的离散时间信号。 8
8 信号分类Ⅲ • 连续时间信号 – 模拟信号 • 时间和幅值都连续的信号。 – 阶梯信号 • 时间连续,幅值离散的信号。 • 离散时间信号 – 抽样信号 • 幅值具有无限精度的离散时间信号。 – 数字信号 • 幅值具有有限精度的离散时间信号。 2 3 1 2 t o 1 抽样信号

典型确定性信号 ·1.f(t)=Kem ·2.f(t)=Asin(ot+0) ·3W=日sle+e8 ,t<0 ·4.f(t)=Ke,s=o+j0,t∈(-o,+∞) -Ke cosot+ike sinot 9
9 典型确定性信号 • 1. • 2. • 3. • 4. t f t Ke f t A t sin 0 , 0 sin , 0 t t f t A t e t , , , st f t Ke s j t cos sin t t Ke t jKe t

典型确定性信号 Sa(t) ·5.r0-a00 -采样函数Sa(t)为偶函数 一在的正、负两方向振幅都 逐渐衰减,当=士π, 代 士2π,,士nπ时,函数值 为零。 ∫Sa)at= π ∫Sa(o)at=元 Sa(t)dt=0 10
10 典型确定性信号 • 5. – 采样函数Sa(t)为偶函数 – 在t的正、负两方向振幅都 逐渐衰减,当t=±π, ±2π,…, ± nπ时,函数值 为零。 sin t f t Sa t t t 1 2 3 -2 4 -3 -4 Sa(t) 0 ( ) 2 ( ) ( ) Sa t dt Sa t dt Sa t dt

典型确定性信号 ·6f(t)=Ee 一高斯函数比任何一个多项 式的倒数衰减都快, ,是个高阶无穷小量。 f(t) i=0 高斯函数的傅里叶变换仍 为高斯的。 一高斯函数为正实函数。 光滑函数C(2):2上任意阶导数都存在的函数的 集合。 11
11 典型确定性信号 • 6 – 高斯函数比任何一个多项 式的倒数衰减都快, 是一个高阶无穷小量。 – 高斯函数的傅里叶变换仍 为高斯的。 – 高斯函数为正实函数。 • t E o f(t) E e 2 t f t Ee 0 ( ) n i i i f t t C 光滑函数 : 上任意阶导数都存在的函数的 集合