中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第七章 离散信号、离散系统

第七章离散信号、离散系统 ·§7.1基本概念 ·§7.2线性定常系统差分方程的解 ·§7.3卷积 2

2 第七章 离散信号、离散系统 • §7.1 基本概念 • §7.2 线性定常系统差分方程的解 • §7.3 卷积

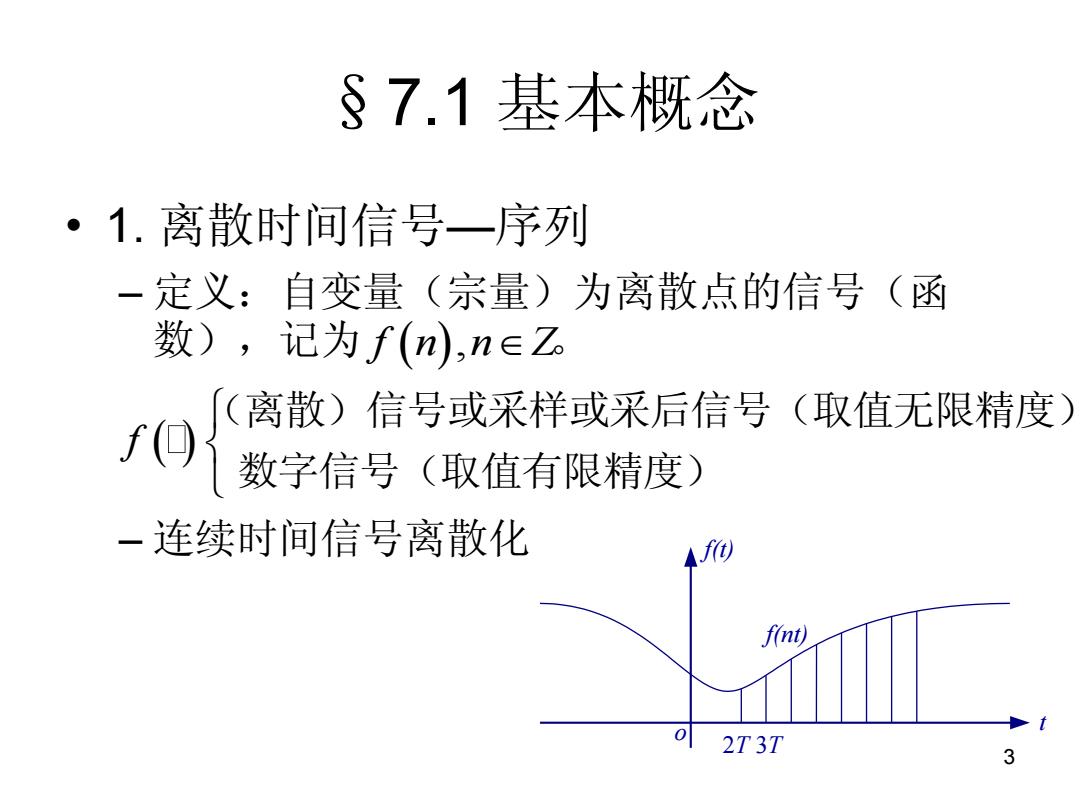
§7.1基本概念 ·1.离散时间信号一序列 一定义：自变量（宗量）为离散点的信号（函 数)，记为f(n),n∈Z 「（离散）信号或采样或采后信号（取值无限精度） 数字信号（取值有限精度） 一连续时间信号离散化 fmt) 0 2T3T

3 §7.1 基本概念 • 1. 离散时间信号—序列 – 定义：自变量（宗量）为离散点的信号（函 数），记为 。 – 连续时间信号离散化 f n n Z  ,  f      （离散）信号或采样或采后信号（取值无限精度） 数字信号（取值有限精度） f(t) t o 2T 3T f(nt)

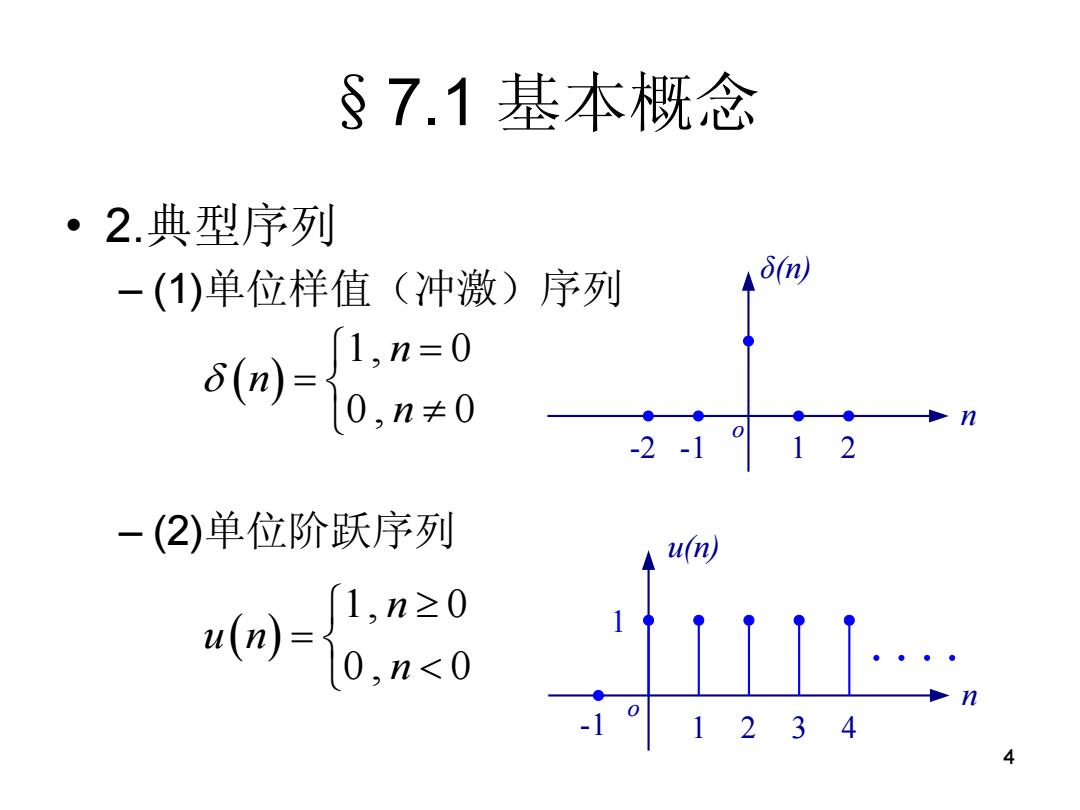
§7.1基本概念 ·2.典型序列 一(1)单位样值（冲激）序列 (n 0-6.a8 2 一(2)单位阶跃序列 u(n) jo -1o1234 4

4 §7.1 基本概念 • 2.典型序列 – (1)单位样值（冲激）序列 – (2)单位阶跃序列   1, 0 0 , 0 n n n        o n -2 -1 1 2 δ(n)   1, 0 0 , 0 n u n n       o n -1 1 2 u(n) 3 4 1

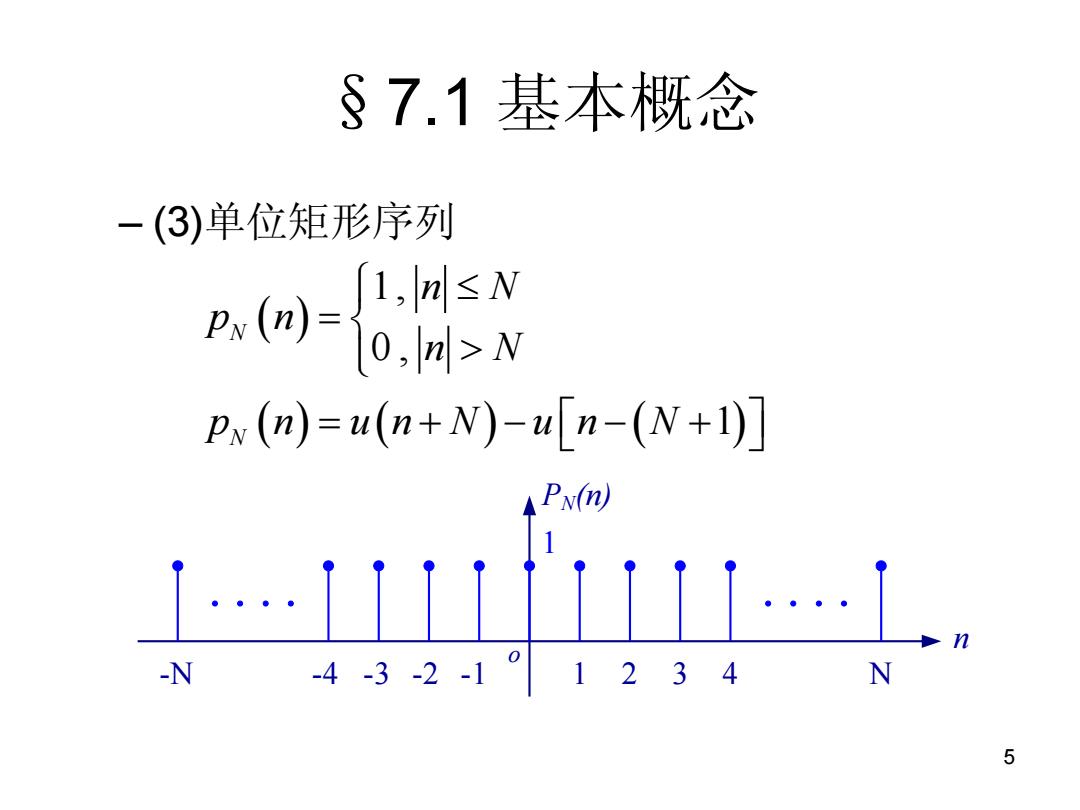
§7.1基本概念 -(3)单位矩形序列 1,m≤N p(网=o,m>N Px (n)=u(n+N)-u[n-(N+1) PN( 11i…1 -N -4-3-2-101234 N 5

5 §7.1 基本概念 – (3)单位矩形序列         1 , 0 , 1 N N n N p n n N p n u n N u n N                  o n -1 1 2 PN(n) 3 4 1 -N -4 -3 -2 N

§7.1基本概念 -(4)正弦序列 2π x(n)=sinnoo=sinnT To -(5)复指数序列 x(n）=ea=x(n)eeaj x(n)=1,arg [x(n)=n@, 6

6 §7.1 基本概念 – (4)正弦序列 – (5)复指数序列   0 0 2 x n n nT sin sin T               0 j jarg 0 1,arg n x n x n e x n e x n x n n              

§7.1基本概念 ·3.信号分解 toio-o)-0n” x(n)=∑x(m)6(n-m) 1三-00 口x(n)*δ(n)…卷积和 7

7 §7.1 基本概念 • 3.信号分解                 , 0 , m x n m n x m n m m n x n x m n m x n n                 卷积和

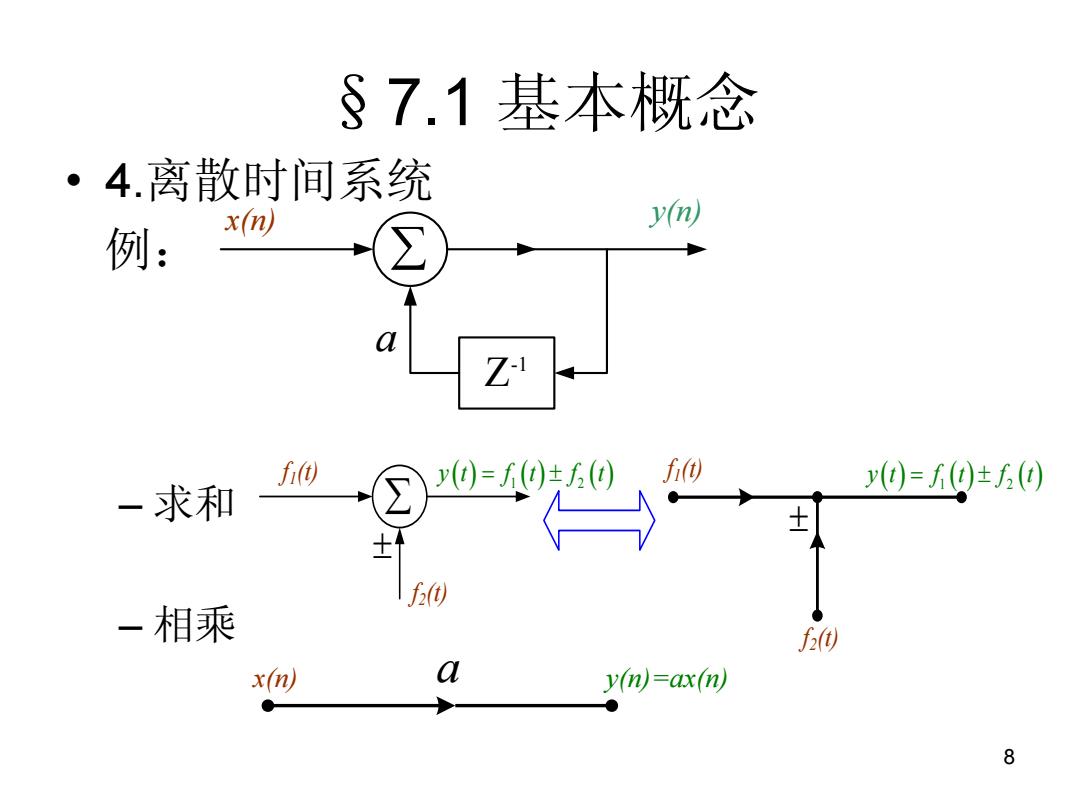
§7.1基本概念 ·4.离散时间系统 y(n) 例： x(n) a Z f ⑨=)生6)、 f似 一求和 0=f0±0 f) 一相乘 f0 x(n) a y(n)=ax(n) 8

8 §7.1 基本概念 • 4.离散时间系统 例： – 求和 – 相乘 x(n)  Z-1 y(n) a f1(t)  f2(t)        1 2 y t f t f t   f1(t) f2(t)       1 2 y t f t f t    x(n) a y(n)=ax(n)

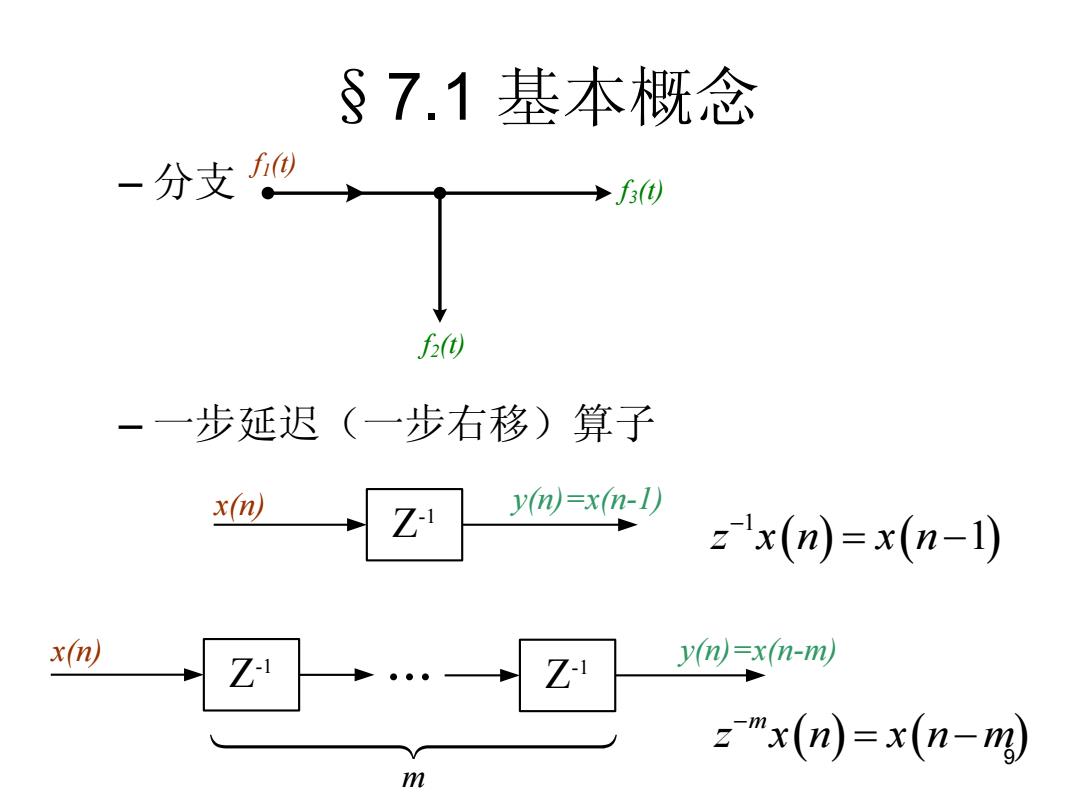
§7.1基本概念 -分支心 →f f6) 一一步延迟（一步右移）算子 x☑ Z y(n)=x(n-1) z'x(n)=x(n-l1） x(n) Z Z y(n)=x(n-m) ="x(n)=x(n-m) m

9 §7.1 基本概念 – 分支 – 一步延迟（一步右移）算子 f1(t) f2(t) f3(t) x(n) Z -1 y(n)=x(n-1) x(n) Z -1 y(n)=x(n-m) Z ... -1 m     1 z x n x n 1        m z x n x n m   

§7.1基本概念 -一步导前（一步左移）算子：x(n)=x(n+I) -例： y(n)=ay(n-1)+x(n) y(n)-av(n-1)=x(n) 若n递减则为后向差分方程；若n递增则为前 向差分方程。 y(n) bo -例：x(n Z b a y(n)=ay(n-1)+azy(n-2)+bx(n)+bx(n-1) y(n)-ay(n-1)-azy(n-2)=box(n)+bx(n-1) 10

10 §7.1 基本概念 – 一步导前（一步左移）算子 ： – 例： 若n递减则为后向差分方程；若n递增则为前 向差分方程。 – 例： zx n x n      1             1 1 y n ay n x n y n ay n x n       x(n) y(n) b0 Z b1 -1 Z-1 Z-1 a1 a2                     1 2 0 1 1 2 0 1 1 2 1 1 2 1 y n a y n a y n b x n b x n y n a y n a y n b x n b x n              

§7.1基本概念 -零状态：y(-1),y(-2),…,y(-N)=0 ∑ay(n-k)=∑bx(n-r） k=0 -零状态线性系统：x(n) L y y(n)=Lx(n) 线性L∑a,x(n)=∑a,Lx(n) i=l y(n-k)==y(n),x(n-r)=zx(n) 含a-会例 11

11 §7.1 基本概念 – 零状态： – 零状态线性系统：           0 0 1 , 2 , , 0 N M k r k r y y y N a y n k b x n r            L x n  y n                      1 1 0 0 L L L , N N i i i i i i k r N M k r k r k r y n x n x n x n y n k z y n x n r z x n a z y n b z x n                                  线性 由