
工程经济学 复习课
工程经济学 复习课

例题1 某工程国家要求建成投产前的投资总额不能超 过3000万元,3年建成。按计划分配,第1年投 资1200万元,第2年投资1000万元,第3年投资 800万元,建设银行贷款年利率为8%,则每年 实际可用于建设工程的投资现金金额及实际应 用建设的投资现值总额为多少?
例题1 某工程国家要求建成投产前的投资总额不能超 过3000万元,3年建成。按计划分配,第1年投 资1200万元,第2年投资1000万元,第3年投资 800万元,建设银行贷款年利率为8%,则每年 实际可用于建设工程的投资现金金额及实际应 用建设的投资现值总额为多少?

例题1 P=1200/(1+0.08)3+1000/(1+0.08)2+800/(1+0 .08)=2550.68(万元) 由计算可知工程建设时所花的总投资为 3000万元,实际用在工程建设上的只有 2550.68万元,其余449.32万元交了利息,占 投资总额的4.977%,可见缩短建设周期的重要 性
例题1 P=1200/(1+0.08)3+1000/(1+0.08)2+800/(1+0 .08)=2550.68(万元) 由计算可知工程建设时所花的总投资为 3000万元,实际用在工程建设上的只有 2550.68万元,其余449.32万元交了利息,占 投资总额的4.977%,可见缩短建设周期的重要 性
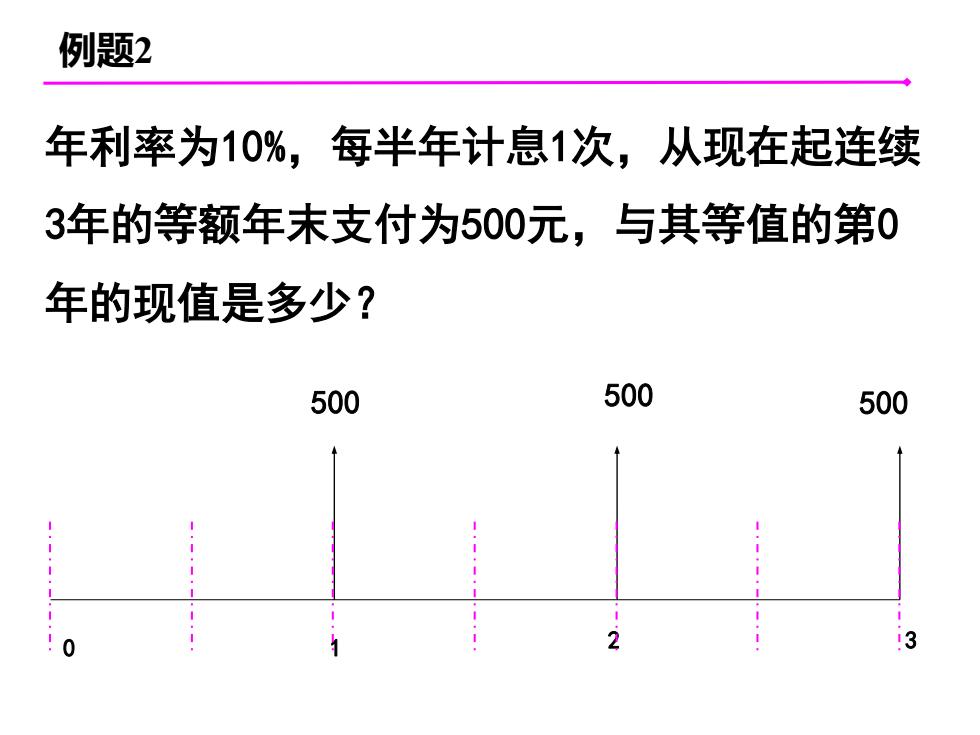
例题2 年利率为10%,每半年计息1次,从现在起连续 3年的等额年末支付为500元,与其等值的第0 年的现值是多少? 500 500 500 ! 0 2 3
例题2 年利率为10%,每半年计息1次,从现在起连续 3年的等额年末支付为500元,与其等值的第0 年的现值是多少? 3 0 1 2 500 500 500

例题2 先求有效年利率,再求现值。 有效年利率为: i=(1+r/m)m-1=(1+10%/2)2-1=10.25% P=AX(P/A,i,3)=500×(P/A,10.256,3) =1237.97(元)
例题2 先求有效年利率,再求现值。 有效年利率为: i=(1+r/m)m-1=(1+10%/2)2-1=10.25% P=A×(P/A,i,3)=500×(P/A,10.25%,3) =1237.97(元)

例题2 把等额支付的每一个支付看作为一次支付,利用 一次支付现值公式计算。 P=500X(1+10%/2)-2+500×(1+10%/2)-4 +500×(1+10%/2)-6 =1237.97(元)
例题2 把等额支付的每一个支付看作为一次支付,利用 一次支付现值公式计算。 P=500×(1+10%/2)-2+500×(1+10%/2)-4 +500×(1+10%/2)-6 =1237.97(元)

例题2 取一个循环周期,使这个周期的年末支付变成等值的 计息期末的等额支付系列,从而使计息期和支付期完 全相同,则可将有效利率直接带入公式计算。年末存 款500元的等效方式是在每半年末存入 A=500×(A/F,i,n)=500×(A/F,10%/2,2)=243.9 P=A×(P/A,i,n)=243.9×(P/A,5%,6)=1237.97(元)
例题2 取一个循环周期,使这个周期的年末支付变成等值的 计息期末的等额支付系列,从而使计息期和支付期完 全相同,则可将有效利率直接带入公式计算。年末存 款500元的等效方式是在每半年末存入 A=500×(A/F,i,n)=500×(A/F,10%/2,2)=243.9 P=A×(P/A,i,n)=243.9×(P/A,5%,6)=1237.97(元)
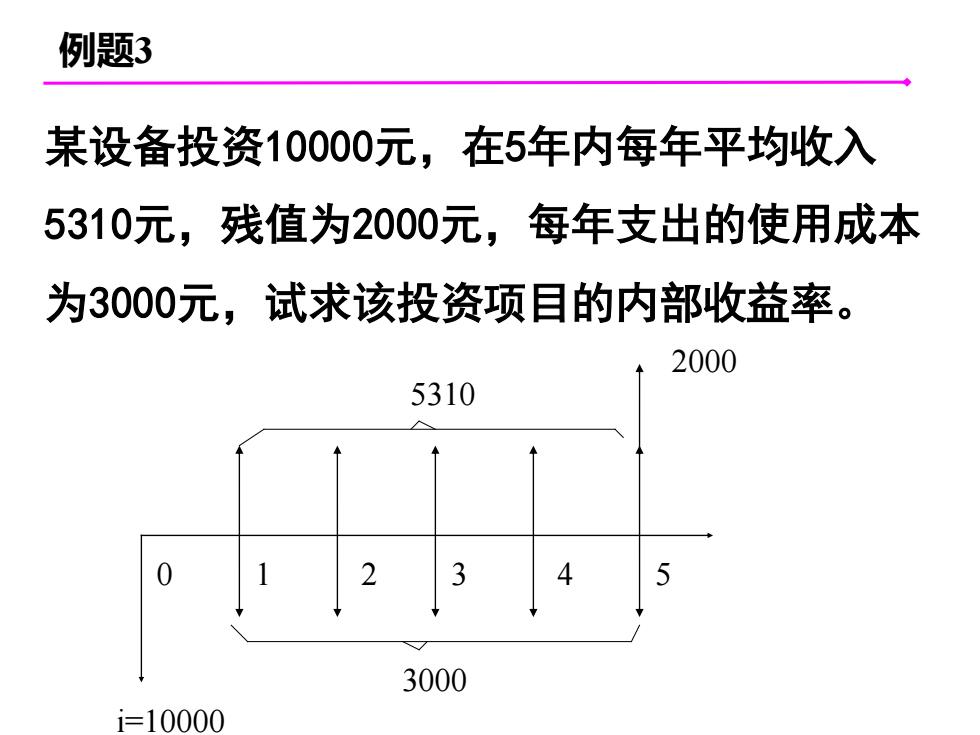
例题3 某设备投资10000元,在5年内每年平均收入 5310元,残值为2000元,每年支出的使用成本 为3000元,试求该投资项目的内部收益率。 2000 5310 4 3000 i=10000
例题3 某设备投资10000元,在5年内每年平均收入 5310元,残值为2000元,每年支出的使用成本 为3000元,试求该投资项目的内部收益率。 i=10000 0 1 2 3 4 5 3000 5310 2000

例题3 。近似确定RR的大致范围 假设=0,P=10000元 ÷F=(5310-3000)×5+2000=13550 (元) 因为(P/P,i,n)=PF, 故(P/F,i,5)=10000/13550=0.738 查表可得,i在6%左右,IRR应大于6%
例题3 ❖近似确定IRR的大致范围 ❖假设i=0,P=10000元 ❖F=(5310-3000)×5+2000=13550(元) ❖因为(P/F,i,n)=P/F, ❖故(P/F,i,5)=10000/13550=0.738 ❖查表可得,i在6%左右,IRR应大于6%

例题3 试算 当试算折现率,=8%时,计算净现值: NPV(i)尸 必 -10000+(5310-3000)P/A,8%,5)+2000(P/F,8%,5) 公 =585.03(元) NPV(i2) -10000+(5310-3000)P/A,12%,5)+2000(P/F,12%,5) =-537.65(元) 用线性插值法求,根据公式: *RR=8%+585.03(12%-8%)=10.08%
例题3 ❖试算 ❖当试算折现率i1=8%时,计算净现值: ❖NPV (i1 )= ❖ -10000+(5310-3000)(P/A,8%,5)+2000 (P/F,8%,5) ❖ =585.03(元) ❖NPV(i2 )= ❖ -10000+(5310-3000)(P/A,12%,5)+2000 (P/F,12%,5) ❖ =-537.65(元) ❖用线性插值法求,根据公式: ❖IRR =8%+585.03(12%-8%)=10.08%