
第三节 敏感性分析 敏感性分析的涵义及作用 在影响技术方案的许多不确定因素中,确定其中一个或几 个发生变化范围的前提下,分析测定技术方案决策目标值对这 些因素变化的反应程度,以判定各因素的变化对目标的重要性 作用: (1)可以确定影响技术方案决策目标值的敏感因素。 敏感因素 非敏感因素 吉林大学管理学院版权所有
吉林大学管理学院版权所有 2 第三节 敏感性分析 一、敏感性分析的涵义及作用 在影响技术方案的许多不确定因素中,确定其中一个或几 个发生变化范围的前提下,分析测定技术方案决策目标值对这 些因素变化的反应程度,以判定各因素的变化对目标的重要性。 作用: (1)可以确定影响技术方案决策目标值的敏感因素。 敏感因素 非敏感因素

对于一般工业投资项目,要作敏感性分析的因素通常有: *投资额,包括固定资产投资与流动资金占用,根据需要可将固定资产 投资划分为设备费用、建筑安装费用等; *项目建设期限、投产期限、投产时的产出能力及达到设计能力所需的时 间; *产品产量及销售量: *产品价格 *经营成本,特别是其中的变动成本 *项目寿命期 *项目寿命期末的资产残值 *折现率 *外币汇率 3 吉林大学管理学院版权所有
吉林大学管理学院版权所有 3 对于一般工业投资项目,要作敏感性分析的因素通常有: *投资额,包括固定资产投资与流动资金占用,根据需要可 将固定资产 投资划分为设备费用、建筑安装费用等; *项目建设期限、投产期限、投产时的产出能力及达到设计能力所需的时 间; *产品产量及销售量; *产品价格 *经营成本,特别是其中的变动成本 *项目寿命期 *项目寿命期末的资产残值 *折现率 *外币汇率

(2)可以测算不确定因素变化对决策目标值的影响程 度,以及不确定因素的临界变化范围,判断方案的风险状 况。 (3)在多方案比较中,通过各方案敏感性程度的比 较,选择敏感度小,风险小的方案作为最优方案。 吉林大学管理学院版权所有
吉林大学管理学院版权所有 4 (2)可以测算不确定因素变化对决策目标值的影响程 度,以及不确定因素的临界变化范围,判断方案的风险状 况。 (3)在多方案比较中,通过各方案敏感性程度的比 较,选择敏感度小,风险小的方案作为最优方案

二、敏感性分析的步骤 1、确定分析目标: 2、选择需要分析的不确定因素; 3、建立分析指标与不确定因素变化的函数关系,并根 据因素的变动幅度,计算分析指标的数值; 4、确定敏感因素,对技术方案风险做出决策。 相对测定法 绝对测定法 5 吉林大学管理学院版权所有
吉林大学管理学院版权所有 5 二、敏感性分析的步骤 1、确定分析目标; 2、选择需要分析的不确定因素; 3、建立分析指标与不确定因素变化的函数关系,并根 据因素的变动幅度,计算分析指标的数值; 4、确定敏感因素,对技术方案风险做出决策。 相对测定法 绝对测定法

敏感性分析,按其因素的多少可分为单因素和多因素 敏感性分析。 三、单因素敏感性分析 单因素敏感性分析是指:单个不确定因素的变动对方 案经济效益的影响所作的分析。(假定其它因素不变)。 在项目评价中,一般是对项目的内部收益率,NPV等 经济评价指标进行敏感性分析。必要时,也可以对投资回 收期等进行敏感性分析。 6 吉林大学管理学院版权所有
吉林大学管理学院版权所有 6 敏感性分析,按其因素的多少可分为单因素和多因素 敏感性分析。 三、单因素敏感性分析 单因素敏感性分析是指:单个不确定因素的变动对方 案经济效益的影响所作的分析。(假定其它因素不变)。 在项目评价中,一般是对项目的内部收益率,NPV等 经济评价指标进行敏感性分析。必要时,也可以对投资回 收期等进行敏感性分析
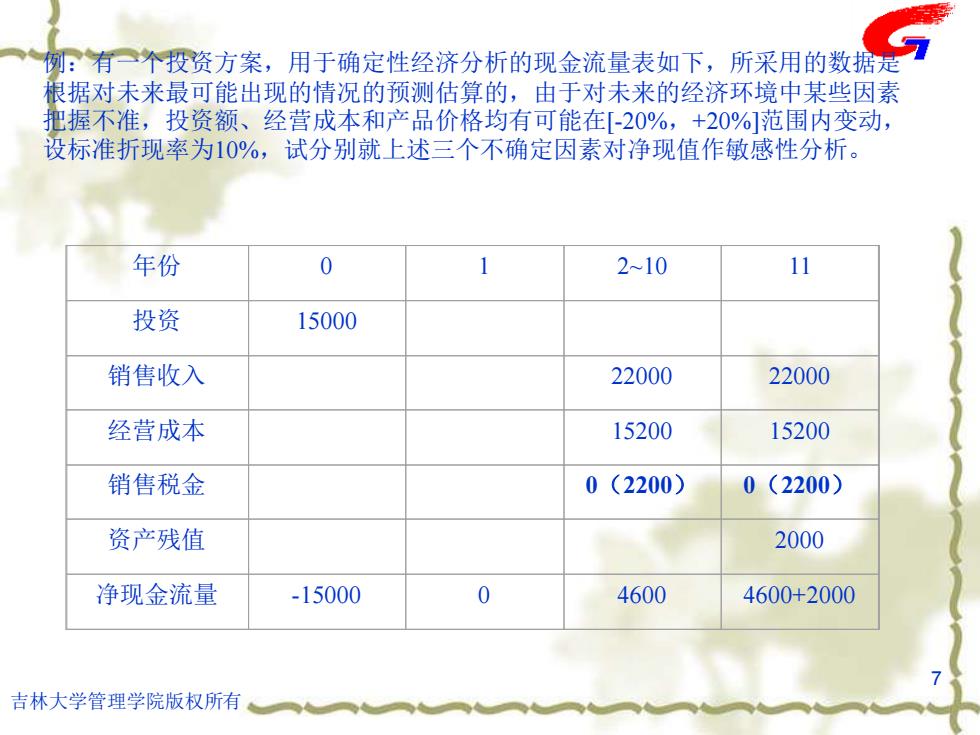
例:有一个投资方案,用于确定性经济分析的现金流量表如下,所采用的数据是 根据对未来最可能出现的情况的预测估算的,由于对未来的经济环境中某些因素 把握不准,投资额、经营成本和产品价格均有可能在[-20%,+20%]范围内变动, 设标准折现率为10%,试分别就上述三个不确定因素对净现值作敏感性分析。 年份 0 2~10 11 投资 15000 销售收入 22000 22000 经营成本 15200 15200 销售税金 0(2200) 0(2200) 资产残值 2000 净现金流量 -15000 0 4600 4600+2000 吉林大学管理学院版权所有
吉林大学管理学院版权所有 7 例:有一个投资方案,用于确定性经济分析的现金流量表如下,所采用的数据是 根据对未来最可能出现的情况的预测估算的,由于对未来的经济环境中某些因素 把握不准,投资额、经营成本和产品价格均有可能在[-20%,+20%]范围内变动, 设标准折现率为10%,试分别就上述三个不确定因素对净现值作敏感性分析。 年份 0 1 2~10 11 投资 15000 销售收入 22000 22000 经营成本 15200 15200 销售税金 0(2200) 0(2200) 资产残值 2000 净现金流量 -15000 0 4600 4600+2000

解:投资额-L 年销售收入-B;年经营成本--C;年销售税金-TA;期 末资产残值--S NPV=-I+(B-C-TA)P/A,0.1,10)P/F,0.1,1)+S(P/F,0.1,11) 设投资额变动百分比为x NPV=-I(1+x)+(B-C-TA)P/A,0.1,10)P/F,0.1,1)+SP/F,0.1,11) 经营成本变动百分比为y NPV=-I+[B-C(1+y)-Ta]P/A,0.1,10)P/F,0.1,1)+SP/F,0.1,11) 产品价格变动的百分比为z NPV=-+[B-Ta)(1+z)-C]P/A,0.1,10)P/F,0.1,1)+SP/E,0.1,11) 8 吉林大学管理学院版权所有
吉林大学管理学院版权所有 8 解:投资额---I; 年销售收入---B; 年经营成本---C; 年销售税金---TA; 期 末资产残值---S. NPV=-I+(B-C-TA)(P/A,0.1,10)(P/F,0.1,1)+S(P/F,0.1,11) 设投资额变动百分比为x NPV=-I(1+x)+(B-C-TA)(P/A,0.1,10)(P/F,0.1,1)+S(P/F,0.1,11) 经营成本变动百分比为y NPV=-I+[B-C(1+y)-TA](P/A,0.1,10)(P/F,0.1,1)+S(P/F,0.1,11) 产品价格变动的百分比为z NPV=-I+[(B -TA)(1+z) -C](P/A,0.1,10)(P/F,0.1,1)+S(P/F,0.1,11)
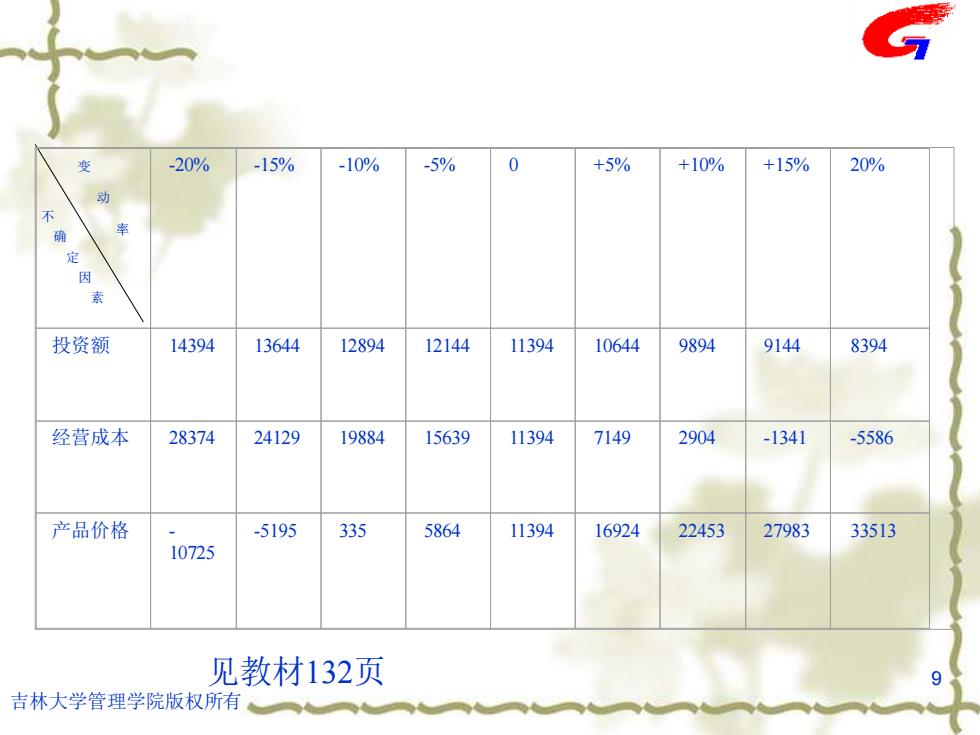
变 -20% -15% -10% -5% 0 +5% +10% +15% 20% 动 率 定 素 投资额 14394 13644 12894 12144 11394 10644 9894 9144 8394 经营成本 28374 24129 19884 15639 11394 7149 2904 -1341 -5586 产品价格 -5195 335 5864 11394 16924 22453 27983 33513 10725 见教材132页 9 吉林大学管理学院版权所有
吉林大学管理学院版权所有 9 变 动 率 不 确 定 因 素 -20% -15% -10% -5% 0 +5% +10% +15% 20% 投资额 14394 13644 12894 12144 11394 10644 9894 9144 8394 经营成本 28374 24129 19884 15639 11394 7149 2904 -1341 -5586 产品价格 - 10725 -5195 335 5864 11394 16924 22453 27983 33513 见教材132页
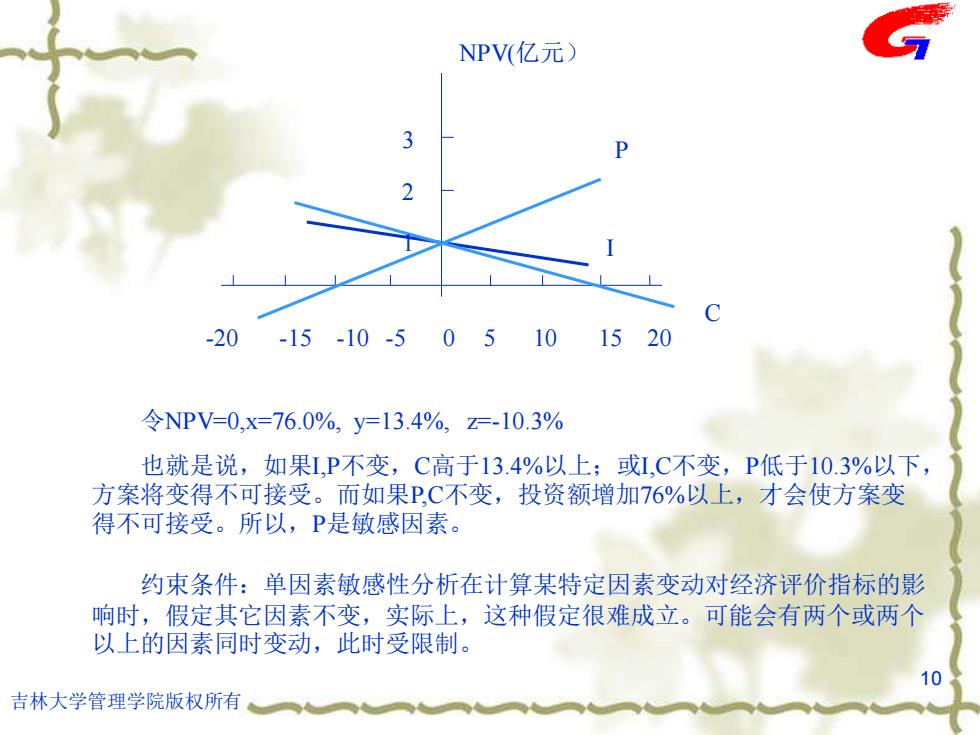
NPV(亿元) 3 -20 -15-10-505101520 令NPV=0,x=76.0%,y=13.4%,z=-10.3% 也就是说,如果I,P不变,C高于13.4%以上;或I,C不变,P低于10.3%以下, 方案将变得不可接受。而如果P,C不变,投资额增加76%以上,才会使方案变 得不可接受。所以,P是敏感因素。 约束条件:单因素敏感性分析在计算某特定因素变动对经济评价指标的影 响时,假定其它因素不变,实际上,这种假定很难成立。可能会有两个或两个 以上的因素同时变动,此时受限制。 10 吉林大学管理学院版权所有
吉林大学管理学院版权所有 10 -20 -15 -10 -5 0 5 10 15 20 1 2 3 NPV(亿元) P I C 令NPV=0,x=76.0%, y=13.4%, z=-10.3% 也就是说,如果I,P不变,C高于13.4%以上;或I,C不变,P低于10.3%以下, 方案将变得不可接受。而如果P,C不变,投资额增加76%以上,才会使方案变 得不可接受。所以,P是敏感因素。 约束条件:单因素敏感性分析在计算某特定因素变动对经济评价指标的影 响时,假定其它因素不变,实际上,这种假定很难成立。可能会有两个或两个 以上的因素同时变动,此时受限制

四、多因素敏感性分析 所谓多因素的敏感性分析,就是在影响方案的多个 不确定因素同时变化的情况下,分析对技术方案决策目标 的影响程度的范围;判断其风险,为科学决策提供依据。 例:根据上例给出的数据进行多因素敏感性分析。 NPV=-I(1+x)+[B-C(1+y)-TA]P/A,0.1,10)P/F,0.1,1)+S(PF,0.1,11) 将表中数据代入,整理得NPV=11394-15000x一84900y 取NPV的临界值】 NPV=0,11394-15000x-84900y=0 y=-0.1767x+0.1342 这是一个直线方程。 11 吉林大学管理学院版权所有
吉林大学管理学院版权所有 11 四、多因素敏感性分析 所谓多因素的敏感性分析,就是在影响方案的多个 不确定因素同时变化的情况下,分析对技术方案决策目标 的影响程度的范围;判断其风险,为科学决策提供依据。 例:根据上例给出的数据进行多因素敏感性分析。 NPV=-I(1+x)+[B-C(1+y)-TA](P/A,0.1,10)(P/F,0.1,1)+S(P/F,0.1,11) 将表中数据代入,整理得 NPV=11394-15000x-84900y 取NPV的临界值 NPV=0, 11394-15000x-84900y=0 y=-0.1767x+0.1342 这是一个直线方程