
年末 方案A 方案B 0 -2000 -2000 1 +1400 +500 2 +800 +700 3 +600 +800 4 +300 +1100 2 吉林大学管理学院版权所有
吉林大学管理学院版权所有 2 年末 方案A 方案B 0 -2000 -2000 1 +1400 +500 2 +800 +700 3 +600 +800 4 +300 +1100

资金时间价值 一、资金的时间价值 1、不同时间发生的等额资金在价值上的差别 2、时间因素的理解: (1)资金增值; (2)必要补偿。 3、影响因素: 投资收益率 通货膨胀 风险因素 3 吉林大学管理学院版权所有
吉林大学管理学院版权所有 3 一、资金的时间价值 1、不同时间发生的等额资金在价值上的差别 2、时间因素的理解: (1)资金增值; (2)必要补偿。 3、影响因素: 投资收益率 通货膨胀 风险因素 资金时间价值

二、利息与利率 利息是指占用资金所付的代价(或放弃使用资 金所获得的补偿)。 如果将一笔资金存入银行,这笔资金称为本金, 经过一段时间之后,储户可在本金之外再得到一笔 利息。 这一过程:F=P+1 Fn-本利和; P.-本金; In-利息。 下标n表示计算利息的周期数。记息周期指计算利息的 时间单位,如年、月等。 利息通常根据利率计算。 吉林大学管理学院版权所有
吉林大学管理学院版权所有 4 二、利息与利率 利息是指占用资金所付的代价(或放弃使用资 金所获得的补偿)。 如果将一笔资金存入银行,这笔资金称为本金, 经过一段时间之后,储户可在本金之外再得到一笔 利息。 这一过程:Fn=P+In Fn ---本利和; P---本金; In ---利息。 下标n表示计算利息的周期数。记息周期指计算利息的 时间单位,如年、月等。 利息通常根据利率计算

利率是在一个记息周期内所得的利息额与本金之比。 般用百分数表示。表示利率。 i=I,/P×100% 式中,1为一个记息周期的利息。 即利率是单位本金经过一个记息周期后的增值额。 5 吉林大学管理学院版权所有
吉林大学管理学院版权所有 5 利率是在一个记息周期内所得的利息额与本金之比。 一般用百分数表示。i表示利率。 i = I1 /P×100% 式中,I1为一个记息周期的利息。 即利率是单位本金经过一个记息周期后的增值额
三单利与复利 1、单利 单利记息是指仅用本金计算利息,利息不再生利息。 I=P.n:I n个记息周期后的本利和为:F=P(1+in) 我国银行储蓄存款和国库券的利息是以单利计算利息的。 年份 年初欠款 年末欠利息 年末欠本利和 1 P Pi P+Pi=P(1+) 2 P(1+) Pi P(1+i)+Pi=P(1+2i) 3 P(+2) Pi P(1+2i1)+Pi=P(1+3i)) n P[1+(n-1)门 Pi P[1+(n-1)门+Pi=P(1+ni) 吉林大学管理学院版权所有
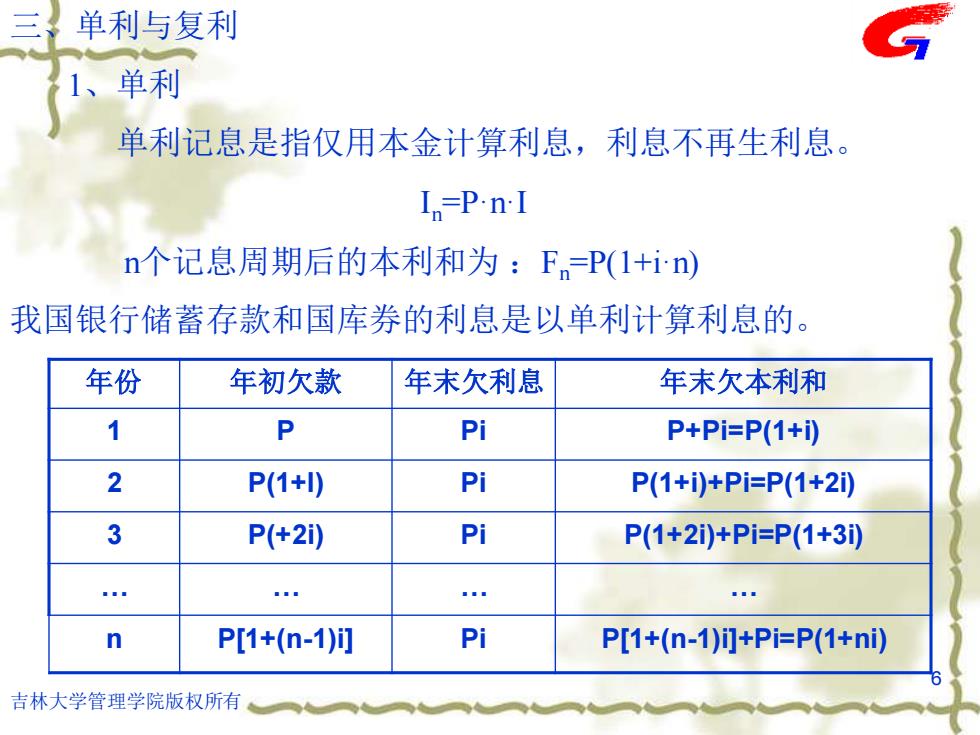
吉林大学管理学院版权所有 6 三、单利与复利 1、单利 单利记息是指仅用本金计算利息,利息不再生利息。 In=P·n·I n个记息周期后的本利和为 :Fn=P(1+i·n) 我国银行储蓄存款和国库券的利息是以单利计算利息的。 年份 年初欠款 年末欠利息 年末欠本利和 1 P Pi P+Pi=P(1+i) 2 P(1+I) Pi P(1+i)+Pi=P(1+2i) 3 P(+2i) Pi P(1+2i)+Pi=P(1+3i) … … … … n P[1+(n-1)i] Pi P[1+(n-1)i]+Pi=P(1+ni)

例4.1:某人买入1000元国库券,年利率为10%,求2年后获得 的总利息,总金额。 解:每年应得利息=1000×10%×1=100(元) 2年总利息=1000×10%×2=200(元) 2年后的总金额=本金+2年总利息=1000+200=1200(元) 单利方式反映在技术经济分析法上是一种半动态。 吉林大学管理学院版权所有
吉林大学管理学院版权所有 7 例4.1:某人买入1000元国库券,年利率为10%,求2年后获得 的总利息,总金额。 解:每年应得利息=1000×10%×1=100(元) 2年总利息=1000×10%×2=200(元) 2年后的总金额=本金+2年总利息=1000+200=1200(元) 单利方式反映在技术经济分析法上是一种半动态

2、复利 当某一记息期的总利息是由本金再加上前一记息期的 总利息来计算时,这种记息方式为复利方式。 F=P(1+i)月 推导: 计息周期n 本利和Fn F=P(1+i) 2 F2=P(1+i)+P(1+i)i=P(1+i)2 3 F3=P(1+i)2+P(1+i)2i=P(1+i)3 n F=P(1+i)1+P(1+i)i=P(1+i) 商业贷款是复利计算的。 复利计算符合扩大再生产的理论与实践,所以常用复利。 8 吉林大学管理学院版权所有
吉林大学管理学院版权所有 8 2、复利 当某一记息期的总利息是由本金再加上前一记息期的 总利息来计算时,这种记息方式为复利方式。 Fn=P(1+i)n 推导: 计息周期 n 1 2 3 … n 本利和Fn F1=P(1+i) F2=P(1+i)+P(1+i)i=P(1+i)2 F3=P(1+i)2+P(1+i)2 i=P(1+i)3 … Fn=P(1+i)n-1+P(1+i)n-1 i=P(1+i)n 商业贷款是复利计算的。 复利计算符合扩大再生产的理论与实践,所以常用复利

例4.2如前例,如果以复利来算,则2年后的利息和 本利和为多少? 解:I=1000×[(1+10%)2-1]=210(元) F=1000(1+10%)2=1210(元) 9 吉林大学管理学院版权所有
吉林大学管理学院版权所有 9 例4.2 如前例,如果以复利来算,则2年后的利息和 本利和为多少? 解:I=1000×[(1+10%)2 -1]=210(元) F=1000(1+10%)2=1210(元)

名义利率与实际利率 ÷例,现有本金100元,给定的年利率为10%,假定 有两种计息周期,一种以年为单位计算利息,一种 以半年为单位计算利息,分别计算一年末的利息额 及其利率 必 解:F(一次)=P(1+)m=100×(1+0.1)1=110 利率1=(110一100)/100=10% ÷F(二次)=P(1+r/m)m=100×(1+0.1/2)2 ÷=100×(1+0.05)2=100×1.052=110.25 ÷利率2=(110.25-100)/100=10.25% 10 吉林大学管理学院版权所有
吉林大学管理学院版权所有 10 名义利率与实际利率 ❖ 例,现有本金100元,给定的年利率为10%,假定 有两种计息周期,一种以年为单位计算利息,一种 以半年为单位计算利息,分别计算一年末的利息额 及其利率。 ❖ 解:F(一次)=P(1+r)m=100×(1+0.1)1=110 ❖ 利率1=(110-100)/100=10% ❖ F(二次)=P(1+r/m)m=100×(1+0.1/2)2 ❖ =100×(1+0.05)2=100×1.052=110.25 ❖ 利率2=(110.25-100)/100=10.25%

名义利率: A当计息周期的时间单位与所给定利率的时间 单位相同时,则所给定的利率就是该时间单位的 名义利率 B当计息周期的时间单位小于所给定利率的时间单位时 ,则名义利率的确定: I确定计息周期的名义利率 10%/2=5% Ⅱ确定给定利率的时间单位的名义利率 1%×12=12% 11 吉林大学管理学院版权所有
吉林大学管理学院版权所有 11 名义利率: A 当计息周期的时间单位与所给定利率的时间 单位相同时,则所给定的利率就是该时间单位的 名义利率。 B 当计息周期的时间单位小于所给定利率的时间单位时 ,则名义利率的确定: I 确定计息周期的名义利率 10%/2=5% II 确定给定利率的时间单位的名义利率 1%×12=12%