
投资方案风险估计一一解析法 条件:方案的经济效果指标(如净现值)服从某种典型概论分 布;期望值与标准差已知 例,假定在上例(书中142页)方案净现值服从正态分布 ,利用其计算结果求:净现值大于或等于0的概率;净现 值小于一100万元的概率;净现值大于或等于500万元的概 率。 解:若连续型随机变量X服从参数为μ,σ的正态分布,X 具有分布函数 (t-4)2 bW=2a 202 dt 吉林大学管理学院版权所有
吉林大学管理学院版权所有 2 投资方案风险估计--解析法 条件:方案的经济效果指标(如净现值)服从某种典型概论分 布;期望值与标准差已知 例,假定在上例(书中142页)方案净现值服从正态分布 ,利用其计算结果求:净现值大于或等于0的概率;净现 值小于-100万元的概率;净现值大于或等于500万元的概 率。 解:若连续型随机变量X服从参数为μ,σ的正态分布,X 具有分布函数 F x dt x t − − − = 2 2 2 ( ) 2 1 ( )

冷正山上式可化为标准正态分布函数 0-,5总m=52 x-u 令Z=X二μ 由正态分布表查出x<X的概率值 0 P(x<x)=P(Z<-兴)=D() 假设方案的净现值是连续型随机变量, u=E(NPV)=232.83(万元),o=σ(NPV)=246.39(万元)则 NPV-E(NPV) NPV-232.83 Z= (NPV) 246.39 3 吉林大学管理学院版权所有
吉林大学管理学院版权所有 3 令u= t- μ σ 上式可化为标准正态分布函数 ( ) 2 1 ( ) 2 2 − = = − − − x F x du x u 令Z= x- μ σ ,由正态分布表查出x<x0的概率值 ( ) ( ) ( ) 0 0 0 − = − = x x P x x P Z 假设方案的净现值是连续型随机变量, μ=E(NPV)=232.83(万元), σ = σ(NPV)=246.39(万元) 则 246.39 232.83 ( ) ( ) − = − = NPV NPV NPV E NPV Z

净现值大于或等于0的概率 P(NPV≥0)=1-P(NPV<0) =1-P(z< 0-232.8 )=1-P(Z<-0.9450)=P(Z<0.9450)=0.8276 246.39 净现值小于一100万元的概率 PWPV<-100)=P(Z<-100-232.83 246.39 =P(Z<-1.351)=1-P(Z<1.351)=1-0.9115=0.0885 净现值大于或等于500万元的概率 P(NPV≥500)=1-P(NPV<500) =1-Pz< 500-232.83 =1-P(Z<1.084)=1-0.8608=0.1392 246.39 正态分布条件下,μ士ō范围内的概率为68.3% u士2σ范围内的概率为95.4% u±3σ范围内的概率为99.7% 吉林大学管理学院版权所有
吉林大学管理学院版权所有 4 净现值大于或等于0的概率 ) 1 ( 0.9450) ( 0.9450) 246.39 0 232.83 1 ( ( 0) 1 ( 0) = − − = − = − = − P Z P Z P Z P NPV P NPV 净现值小于-100万元的概率 ( 1.351) 1 ( 1.351) 1 0.9115 0.0885 ) 246.39 100 232.83 ( 100) ( = − = − = − = − − − = P Z P Z P NPV P Z 净现值大于或等于500万元的概率 ) 1 ( 1.084) 1 0.8608 0.1392 246.39 500 232.83 1 ( ( 500) 1 ( 500) = − = − = − = − = − P Z P Z P NPV P NPV 正态分布条件下, μ±σ范围内的概率为68.3% μ±2σ范围内的概率为95.4% μ±3σ范围内的概率为99.7% =0.8276

投资方案风险估计一一图示法 序号 状态组合 净现值NPVO 发生概率P 累计概率 (i=12%) 1 Om3NOr1 -170.98 0.08 0.08 2 OminO2 -98.81 0.08 0.16 3 OmnO -26.71 0.04 0.20 4 Omne1 117.48 0.24 0.44 5 OmNO2 261.67 0.24 0.68 6 0m2∩Oeg 405.86 0.12 0.80 7 0m∩Oi 405.86 0.08 0.88 8 ⊙ming2 622.15 0.08 0.96 9 ⊙m1∩03 838.44 0.04 1.00 5 吉林大学管理学院版权所有
吉林大学管理学院版权所有 5 投资方案风险估计--图示法 序号 状态组合 净现值NPV(j) (i0=12%) 发生概率Pj 累计概率 1 Θm3∩Θr1 -170.98 0.08 0.08 2 Θm3∩Θr2 -98.81 0.08 0.16 3 Θm3∩Θr3 -26.71 0.04 0.20 4 Θm2∩Θr1 117.48 0.24 0.44 5 Θm2∩Θr2 261.67 0.24 0.68 6 Θm2∩Θr3 405.86 0.12 0.80 7 Θm1∩Θr1 405.86 0.08 0.88 8 Θm1∩Θr2 622.15 0.08 0.96 9 Θm1∩Θr3 838.44 0.04 1.00
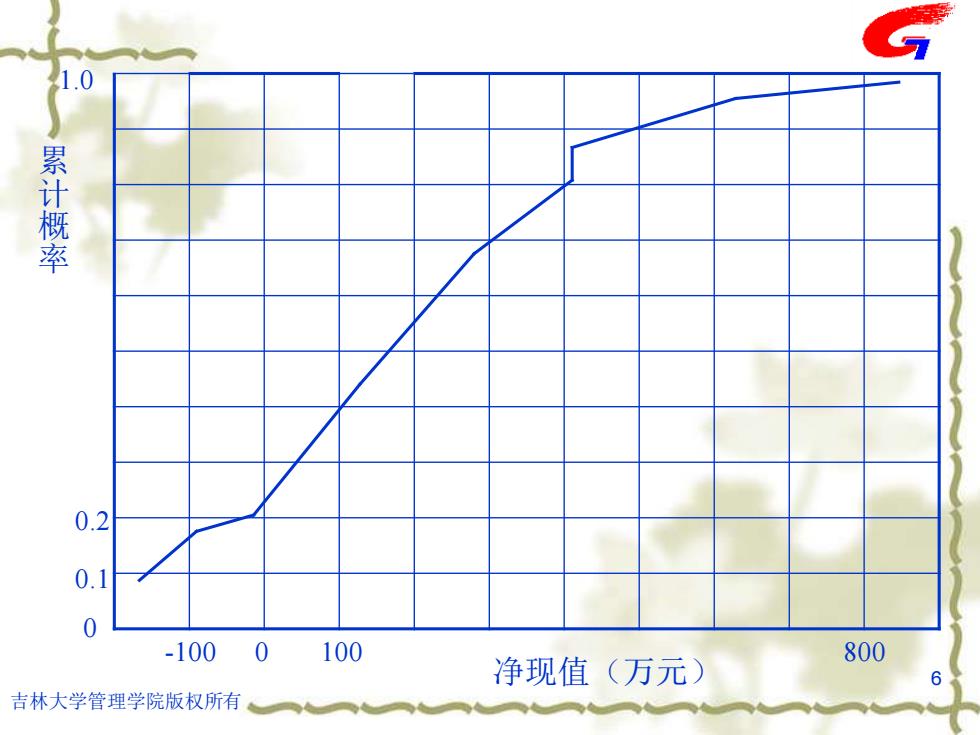
1.0 累计概率 0.2 0.1 0 -100 0 100 800 净现值(万元) 6 吉林大学管理学院版权所有
吉林大学管理学院版权所有 6 0 0.1 -100 0 100 1.0 累 计 概 率 净现值(万元) 800 0.2
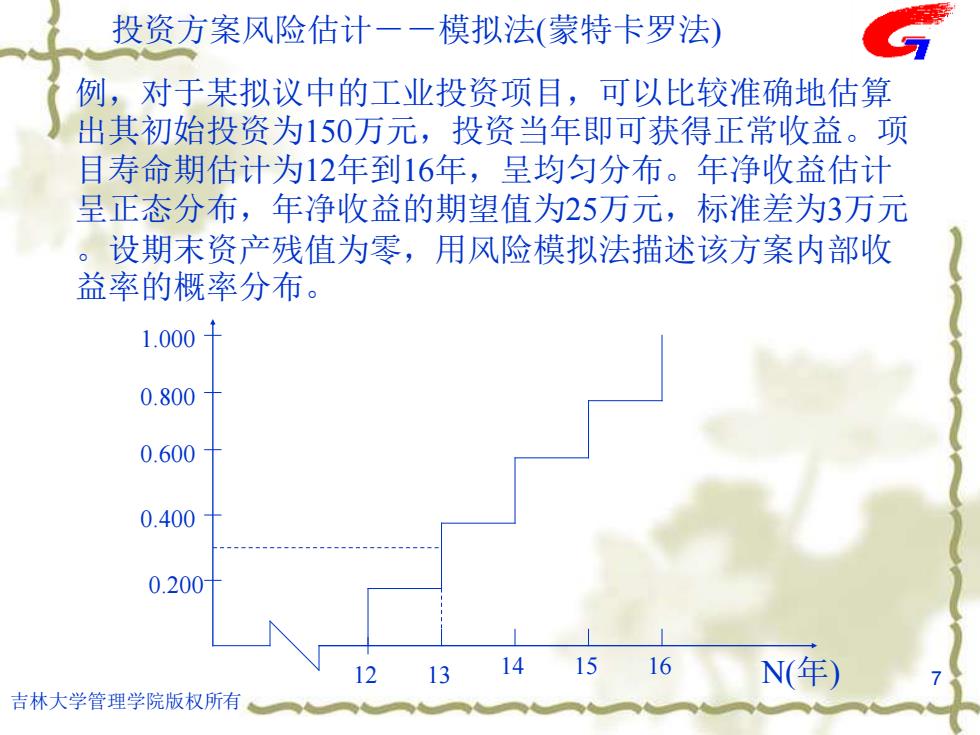
投资方案风险估计一一模拟法(蒙特卡罗法) 例,对于某拟议中的工业投资项目,可以比较准确地估算 出其初始投资为150万元,投资当年即可获得正常收益。项 目寿命期估计为12年到16年,呈均匀分布。年净收益估计 呈正态分布,年净收益的期望值为25万元,标准差为3万元 设期末资产残值为零,用风险模拟法描述该方案内部收 益率的概率分布。 1.000 0.800 0.600 0.400 0.200 1213 14 1516 N(年) 吉林大学管理学院版权所有
吉林大学管理学院版权所有 7 投资方案风险估计--模拟法(蒙特卡罗法) 例,对于某拟议中的工业投资项目,可以比较准确地估算 出其初始投资为150万元,投资当年即可获得正常收益。项 目寿命期估计为12年到16年,呈均匀分布。年净收益估计 呈正态分布,年净收益的期望值为25万元,标准差为3万元 。设期末资产残值为零,用风险模拟法描述该方案内部收 益率的概率分布。 0.200 0.600 0.400 0.800 1.000 12 13 14 15 16 N(年)
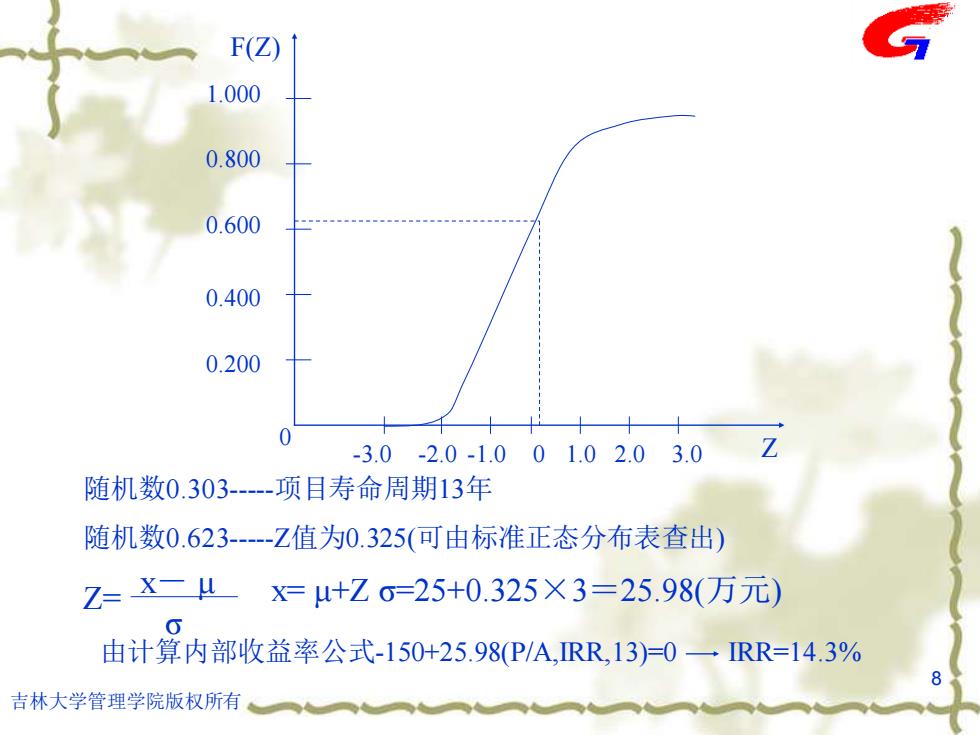
F(Z) 1.000 0.800 0.600 0.400 0.200 0 -3.0-2.0-1.001.02.03.0 Z 随机数0.303--项日寿命周期13年 随机数0.623--Z值为0.325(可由标准正态分布表查出) Z=X二L x=u+Z0=25+0.325X3=25.98(万元) 0 由计算内部收益率公式-150+25.98(P/A,RR,13)=0一RR=14.3% 8 吉林大学管理学院版权所有
吉林大学管理学院版权所有 8 0 -3.0 -2.0 -1.0 0 1.0 2.0 3.0 0.200 0.400 0.600 0.800 1.000 Z F(Z) 随机数0.303-----项目寿命周期13年 随机数0.623-----Z值为0.325(可由标准正态分布表查出) x- μ σ Z= x= μ+Z σ=25+0.325×3=25.98(万元) 由计算内部收益率公式-150+25.98(P/A,IRR,13)=0 IRR=14.3%
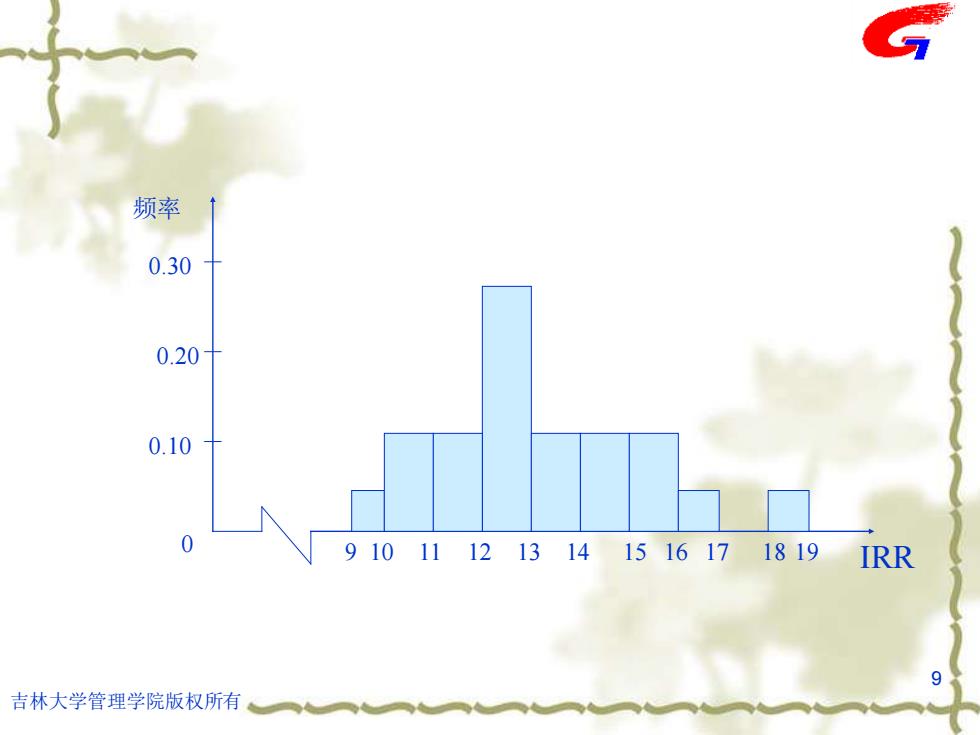
频率 0.30 0.20 0.10 910111213141516171819 IRR 9 吉林大学管理学院版权所有
吉林大学管理学院版权所有 9 频率 IRR 0 9 10 11 12 13 14 15 16 17 18 19 0.10 0.20 0.30

风险决策 风险决策的条件 1、存在着决策人希望达到的目标 2、存在着两个或两个以上的方案可供选择 3、存在着两个或两个以上不以决策者的主观意志为转 移的自然状态 4、可以计算出不同方案在不同自然状态下的损益值 5、在可能出现的不同自然状态中,决策者不能肯定未 来将出现哪种状态,但能确定每种状态出现的概率 10 吉林大学管理学院版权所有
吉林大学管理学院版权所有 10 风险决策 风险决策的条件 1、存在着决策人希望达到的目标 2、存在着两个或两个以上的方案可供选择 3、存在着两个或两个以上不以决策者的主观意志为转 移的自然状态 4、可以计算出不同方案在不同自然状态下的损益值 5、在可能出现的不同自然状态中,决策者不能肯定未 来将出现哪种状态,但能确定每种状态出现的概率
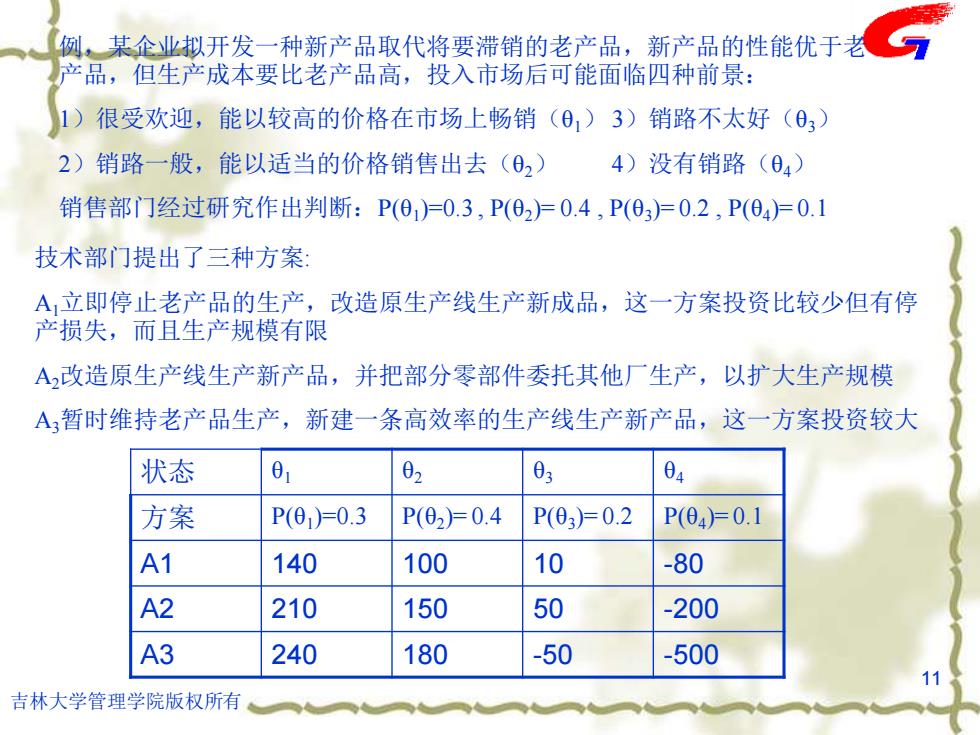
例,某企业拟开发一种新产品取代将要滞销的老产品,新产品的性能优于老 产品,但生产成本要比老产品高,投入市场后可能面临四种前景: 1)很受欢迎,能以较高的价格在市场上畅销(θ,)3)销路不太好(0) 2)销路一般,能以适当的价格销售出去(02) 4)没有销路(04) 销售部门经过研究作出判断:P(0)=0.3,P(02)=0.4,P(03)广0.2,P(04)=0.1 技术部门提出了三种方案: A立即停止老产品的生产,改造原生产线生产新成品,这一方案投资比较少但有停 产损失,而且生产规模有限 A改造原生产线生产新产品,并把部分零部件委托其他厂生产,以扩大生产规模 A暂时维持老产品生产,新建一条高效率的生产线生产新产品,这一方案投资较大 状态 01 02 03 04 方案 P(0)=0.3 P(02)F0.4 P(03)=0.2 P(04)=0.1 A1 140 100 10 -80 A2 210 150 50 -200 A3 240 180 -50 -500 11 吉林大学管理学院版权所有
吉林大学管理学院版权所有 11 例,某企业拟开发一种新产品取代将要滞销的老产品,新产品的性能优于老 产品,但生产成本要比老产品高,投入市场后可能面临四种前景: 1)很受欢迎,能以较高的价格在市场上畅销(θ1) 3)销路不太好(θ3) 2)销路一般,能以适当的价格销售出去(θ2) 4)没有销路(θ4) 销售部门经过研究作出判断:P(θ1 )=0.3 , P(θ2 )= 0.4 , P(θ3 )= 0.2 , P(θ4 )= 0.1 技术部门提出了三种方案: A1立即停止老产品的生产,改造原生产线生产新成品,这一方案投资比较少但有停 产损失,而且生产规模有限 A2改造原生产线生产新产品,并把部分零部件委托其他厂生产,以扩大生产规模 A3暂时维持老产品生产,新建一条高效率的生产线生产新产品,这一方案投资较大 状态 θ1 θ2 θ3 θ4 方案 P(θ1 )=0.3 P(θ2 )= 0.4 P(θ3 )= 0.2 P(θ4 )= 0.1 A1 140 100 10 -80 A2 210 150 50 -200 A3 240 180 -50 -500