
第八章单室模型
第八章 单室模型

单室模型: 。某些药物进入体内后迅速向全身组织器 官分布,并迅速达到分布动态平衡 ·此时整个机体可视为一个隔室 ·依此建立的药动学模型称为单室模型
单室模型: • 某些药物进入体内后迅速向全身组织器 官分布,并迅速达到分布动态平衡 • 此时整个机体可视为一个隔室 • 依此建立的药动学模型称为单室模型

第一节静脉注射 一、血药浓度 二、尿药浓度 1.尿排泄速度与时间的关系 2.尿排泄量与时间关系 3.肾清除率
第一节 静脉注射 一、血药浓度 二、尿药浓度 1. 尿排泄速度与时间的关系 2. 尿排泄量与时间关系 3. 肾清除率
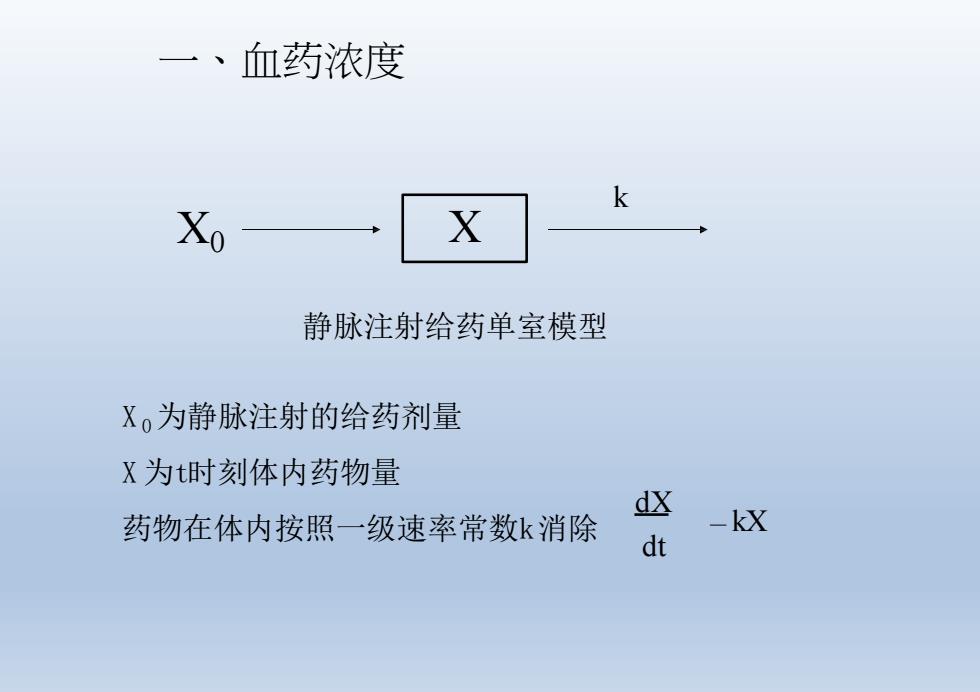
一、血药浓度 k Xo X 静脉注射给药单室模型 X。为静脉注射的给药剂量 X为时刻体内药物量 d必 药物在体内按照一级速率常数k消除 _kX dt
一、血药浓度 X 0为静脉注射的给药剂量 X 为t时刻体内药物量 药物在体内按照一级速率常数k消除 X0 X k 静脉注射给药单室模型 kX dX dt
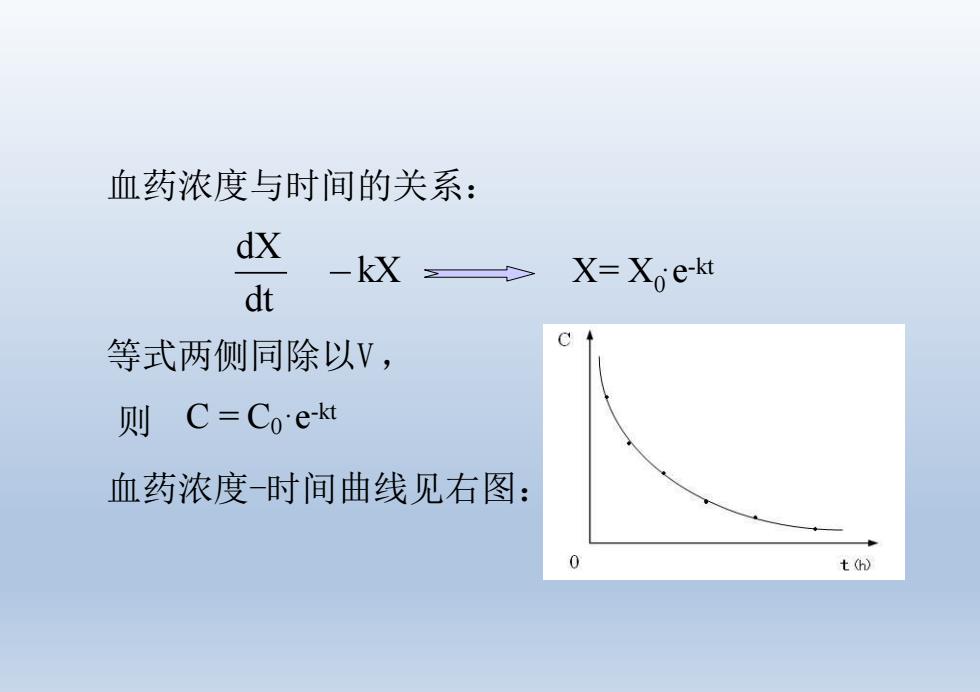
血药浓度与时间的关系: dX -kX X=Xoe-kt dt 等式两侧同除以V, 则C=Coe-kt 血药浓度-时间曲线见右图: t(h
血药浓度与时间的关系: 等式两侧同除以V, 则 血药浓度-时间曲线见右图: X = X0·e-kt C = C0·e-kt kX dt dX
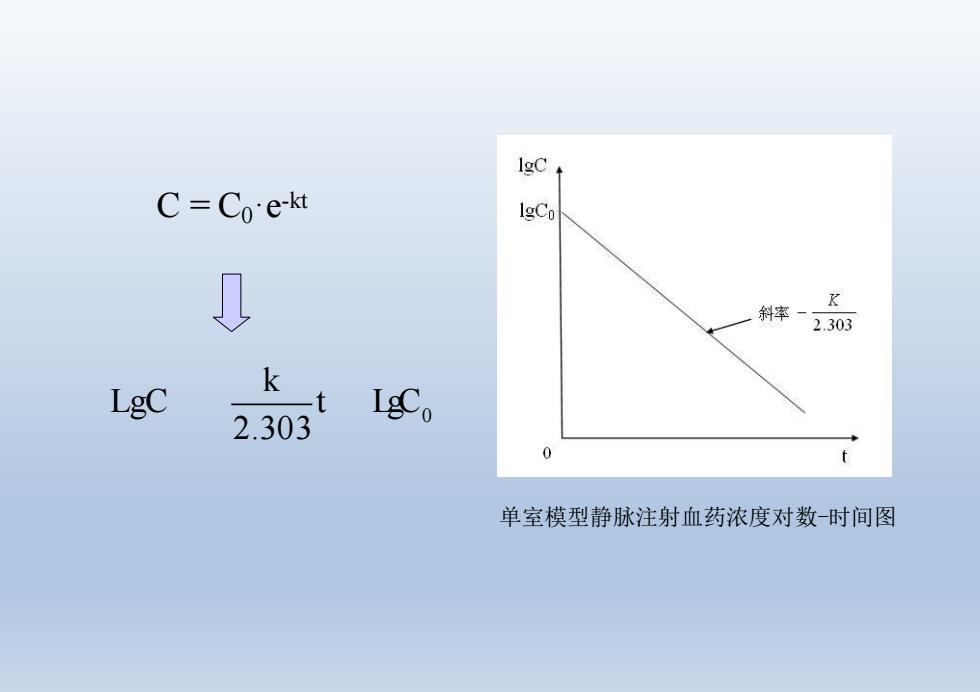
lgCt C e-kt IgCo 0 斜案、 2.303 LgC IgCo t 单室模型静脉注射血药浓度对数-时间图
C = C0·e-kt 0 2.303 k LgC t LgC 单室模型静脉注射血药浓度对数-时间图

·基本参数的求算 1.半衰期(t2):t12表示药物在体内消除一半所 需要的时间。 将t=t12,CC/2代入LgC-t关系式,得: 1g2 2303a+1gC。 0.693 12 k
• 基本参数的求算 1. 半衰期(t1/2):t1/2表示药物在体内消除一半所 需要的时间。 将t=t1/2,C=C0/2代入LgC-t关系式,得: t 1/ 2 □ ln 2 0.693 k k 1/ 2 0 2 2.303 C k lg 0 = - t + lgC

2. 表观分布容积(V):体内药量与血药浓度间相 互关系的一个比例常数。 X C 3.血药浓度时间曲线下面积(AUC) AUC-Cdt =o Coedt-Co
C0 3. 血药浓度-时间曲线下面积(AUC) 2. 表观分布容积(V):体内药量与血药浓度间相 互关系的一个比例常数。 V X 0 AUC = 0 Cdt C ·e 0 0 = k -ktdt = C0
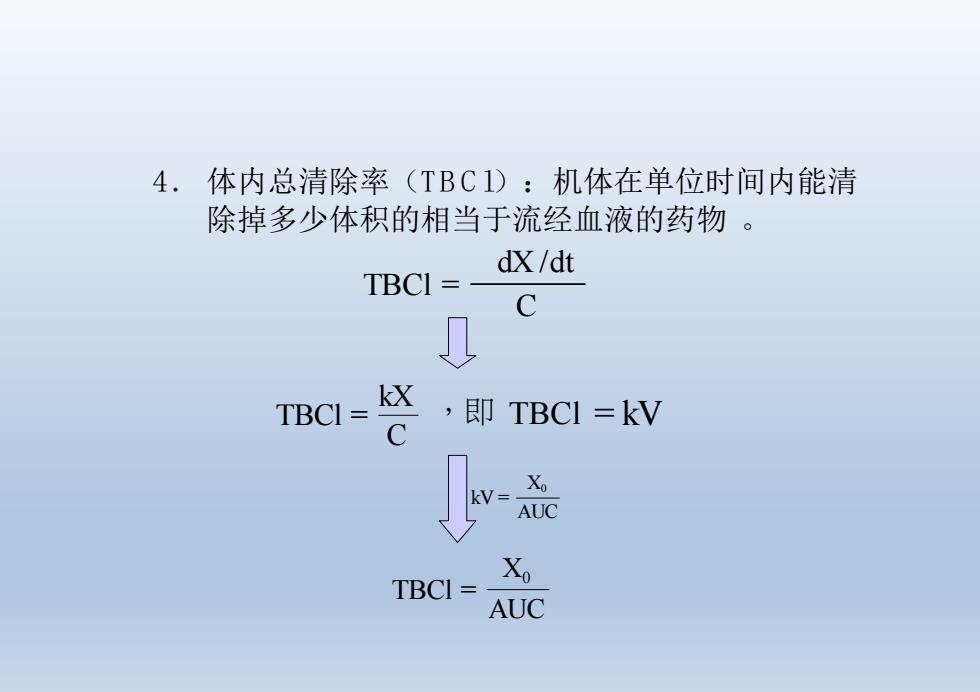
4.体内总清除率(TBC1):机体在单位时间内能清 除掉多少体积的相当于流经血液的药物。 dX/dt TBCI= 0 TBCI= ,即TBC=kV Xo TBCI= AUC
4 . 体内总清除率(T B C l):机体在单位时间内能清 除掉多少体积的相当于流经血液的药物 。 C dX /dt TBCl = C TBCl = kX ,即 TBCl = kV AUC X0 kV = AUC TBCl = X0

讨论: 。V体液总量,说明该药物多被机体的器官、 组织所摄取
讨论: • V<血浆容量,说明该药物分布在血液中; • V = 体液总量,说明该药物在体液分布均匀; • V >体液总量,说明该药物多被机体的器官、 组织所摄取