
第五章时间数列 教学目的与要求:了解动态数列的基本慨念,掌猩动念数列的水平指标及速度指标:理 解动念数列的长期趋势的定量分析法:会运用有关理论进行季节变动的测定与预测 教学重点:动念数列的水平指标及速度指标:动态数列的长期趋势的定量分析法:季节 变动的测定与预测 教学难点:时点数列的半均发展水平指标的计算:平均发展速度的计算:最小二乘法应 用:季节变动的测定与预测 8.1时间数列概述 8.1.1时间数列的概念和构成要素 时间数列是将说明社会经济现象在各个不同时划或时点上某种数量特征的指标数值,按 时间的先后顺子捧列起来而形成的统计数列。山于时间数列中每项数值是与时间相对应的, 所以又称之为动念数列。 一个是资料所属的时间,另一个是各时间上的统计指标 数值。如表8-1即为一个时间数列 表8-1我国国内生产总值基本情况表 单位:亿元 年份19992000200120022003 2004 200520062007 GDP89677.199214.6109655.212033.2135822.8159878.3183217.4211923.5249529.9 :2003中国统计年室中国统计出版社,3 山以上的时间数列,我们可以看出,我国国内生产总值呈逐年增长的趋势。动念分析法 就是应用统计分析方法研究现象总体数量方面随时间变化而变化发展的过程,而时间数列则 是动态分析时必须具备的统计资料。 穷时数列日.右承要的作用。通过时数列的编制知分析折:一可可以招术社会经济得复 发展的过程和结果 可以研究社会经济现象的发尼速度和发尼规律 可以根据时间数列 对现象的发展进行统计预测:四可以利用不同空向范围,但又相互联系的时间数列进行对出 分析或相关分析.简而言之,时间数列有两大类功能:一是对现有的现象进行分析,二是根 据现状对未来进行预测,本章也是用绕这两大类功能展开的。 8.1.2时间数列的种类 时间数列 按其所样列的统计指标数值的不同,可分为绝对数时间数列、相对数时间数列 和平均数时间数列 种。其中,绝对数时间数列是最基本数列,而相对数时间数列和半均数 时间数列则是山绝对数时间数列派生而行出的数列。一种时间数列所表述的现象特性有所 同,三种数列中各项数值的取得和计算方法也有所不同。 1。绝对数时间数列 绝对数时间数列是山一系列同类的总量指标,按者时间的先后顺子排列而成的时间数 列,用以反陕所研究现象的规模或水半的变动情况。 称为总量指标时间数列。如果按照 标所反映的社会经济现象所属的时间不同,绝对数时间数列义可分为时明数列和时点数列两 种。 1)时期数列 在始对数动数列中,如果各项指标都是反映某种现象在一段时内发属时程的总量】

这种绝对动念数列就称为时期数列。如表8-1中所列的我国1998-2006年社会消费品零售总 额就是一个时期数列。时期数列具有以下特点: (1)数列中各个指标的数值是可以相加的,即相加具有一定的经济意义。山于时期数 列中每个指标的数值都是表示在一段时间内发展过程的总量,从本质上讲,属于流量指标, 所以相加后的数值就表示现象在必长一段时间内发展过程的总量。如表8-1中将2001年、 2002年、2003年、2001年、2005年的国内生产总值相加,就是我国“1五”期间国内生产 点值。 (2)数列中每一个指标数值的大小与所属的时期长短有直接的联系。在时期数列中 每个指标所属时间的长度,称为“时期”。时期的长短,主要根据研究目的而定,可以是 山、一旬、一月、一季或史长时期。山于每个指标都是反映现象在某一段时期内发展过程的 总量,除了个别可能出现负值的总量指标,利润总额等,一般来说,时期愈长,指标的数 值就愈大。 (3)数列中每个指标数值,通常是通过连续不断的登记取得的 2)时点数列 在绝对数动念数列中,!果每个指标所反映的现象在某一时点上(瞬间)所处状念的数 量水半,这种绝对数动念数列就称为时点数列。在时点数列中,相邻两个指标值在时间上的 间距称为“向隔” 表8-2我国各年年末人口数 绝位:万 年份 19992000 2001 200220032004205206207 人口数 125786126743127627128453129227129988130756131448132129 资料来源:2008中国统计年鉴.中国统计出版社,87页 从以上数列.反快出我国1999-2007年之间.我国人口弯动的基本情况。h干该数列的 每个指标数值都说明在该年年底时点上的人口数,所以为时点数列。时点数列具有以下特点 (1)数列中每个指标数值除非计算过程需要相加外 般不能相加。山于时点数列 每个指标数值表明在某一时点上现象的数量,从本质上讲,属于存量指标,几个指标相加后 无法说明属于哪一个时点的数量,因此,时点指标相加不具有实际经济意义。 (2)数列中每一个指标数值的大小与其间隔长短没有直接的联系。山于时点数列中每 个指标的数值,只表明现象在某一时点上的数量,因此它的指 数值大小与时向间隔长短没 有直接联系 (3)数列中每个指标数值,通常足间隔一段时间登记一次而取得的 2.相对数时间数列 山一系列同类的相对指标,按者时间同先后顺学排列而成的时间数列.用以反映现象之旧 的数量对比关系或相互联系的发展变化状况及过程,又称为相对指标时间数列。 3我国财 收入 发展速 年份 199819992000200120022003200420052006 财政收入(亿元)8651987611444163861890321715263553051235500 发展速度)-114115117122115121115116 资料未源:2006年:中国经济形势分析与预测 件字文献出版社.339 相对数时间数列是山两个绝对数时间数列对比计算而产生,山于绝对数时间数列可以分 为时期数列和时点数列,因此,相对数时间数列可以山两个时期数列对比所派生,也可以是 两个时点数列对比所派生,或者是一个时期数列和一个时点数列对比所派生。相对数时间数 列中的各个指标数值是不能直接相加的。 3平均 动态数列 山一系列同类的平均数指标数值,按时间先后顺序排列而成的数列,用以反映现象一般

水平的发展变化过程及趋势,又称为平均指标时间数列。 表8-4我国2000一2007年职工年平均工资 单位:元 年份 20002001200220032004200520062007 职工年平均工资937110870124221404016024183642100124932 资料来源:2008中国就计年毫,中国统计出版社,149页, 显然,平均数时间数列中,各个指标数值也是不能相加的,相加后没有实际意义。但有 时为了计算序时平均数 ,在布计算过程中需要相加 为了对社会经济现象发展过程进行全面分析,在实际工作中,上述各种时可数列经常结 合起来进行运用, 8.1.3时间数列的编制原则 编制时问数列的目的,主要是通过数列中各项指标的对比来反映社会经济现象的发展过 程及其规律。因此,保证数列中各项数值之间的可比 ,就应成为正确编制时间数列要遵循 的基本原则。为此,在编制时间数列时必须注意以下几个方面: 1.时期与时间间隔相等 在编制时期数列时,因为时期数列中指标各项数值的大小与时期长短有直接的关系,如 见时期长短不同,指标各项数值之自就无法对比,因此,各个指标所属的时期长短应当前后 但这个原则不能绝对化,有时为了特殊的研究目的,也可将时期不等的指标编成时期 数列。见表8-5所示。 从表8-5资料中,可以明显看出,我国第一个土年计划时期的钢产量超过旧中国将近半 个世纪钢产量1倍以上,第八个五年计划时期钢产量又比“一五”时期有了史快的发展,增 长了24倍以上。 表8-5我国不同历史时期的钢产量 单位:万吨 时期(年) 1900-1948 1953-1957 991-1995 钢产量 780 1667 42708 布编制时点数列时,因为各个指标只反映现象在某 时点的状态,时点数列中指标各项 数值的大小与时点间隔长短无直接关系,所以就不必考虑两个时点之间间隔是杏相等,但为 了史有利于对比,时点向隔最好能保持一致。 需要说明的是,时期相等与间隔相等是两个不同的概念,所谓的时期相等,是指连续累 加计算的时期指标数值的时间长短相等。而所谓的间隔相等,是指相邻两个时点之间的时间 差相等。在资料齐全的情况下, 应尽可能编制时期长短与时间间隔长短都相等的时期数列利 时点数列,这样史有利于说明现象发辰变化的规律性。 2.总体范围一致 所谓总体范用一致,就是在时间数列中要求各项指标数值所包含的总体范围前后应该 致。例如要研究某地区工业生产发展情况。果那个地区的行政区有了变动.则前后指标损 值不能直接对比,在编制时间数列时就要考虑将资料进行适当调整,以求得总体范围的统 这样便于对数列进行动态分析 3.计算方法统 在时间数列中各项指标数值的计算方法和计量单位不统一是不能进行对比分析的。在编 制时间数列时必须做到前后指标数值之间计算口径一致和计量单位的统一。例,要研究企 业劳动生产率的变化,在计算劳动生产率指标时,子项品用实物量指标还是用价值量指标 母项是用全部职工人数还是用生产工人人数,前后一定要统一起来。再如,当我们要用价值

指标编制一个时期较长的时数列时,为保证前后指标数值的可比性,就要注意价格水平的 变化,成采用练一不的价格来表示,使出且有可出性 ,在编制时间数列时 如果出现个可比的情况,就应加以调整使其可比。但是我们 也不能把可比性绝对化,主要取决于统计研究的日的,决定其是古可比。 8.2时间数列水平指标 时数列描术了现象的发展过程和结果,但必还不能直接反映现象各期的增数量 变动速度和规律性,为深刻提示现象的这些特征,需计算一系列的动态分析指标,常用的有 发尼水半、平均发展水半、增长量、半均增长量:发展速度、增长速度、半均发尼速度、 均增长速度等。其中前四种称为动态分析的水半指标,后四种称为动念分析的速度指标。我 们将分别在8.2、8.3两节中予以分析。 8.2.1发展水平 时间数列中按时间顺序记录下来的,反映现象在不同时期或时点所达到的水平的指标 值就是发展水半,它可以是总量指标、 相对指标或平均指标。发展水平是计算其它动态分村 指标的基础。根据各指标值在时间数列中所处的位咒,通常把时间数列中的第 一个指标值移 为最初水半,最后一个指标值称为最木水半,其他中间各指标值称为中间水半。在对比时间 数列中的两个发展水平时,把用做比较基础的数值称为基础发展水半,把要分析计算的那 时间上的指标数值称为报告期发展水平,如果用符号代表各期的发展水半,则a,a α就代表数列中各期的发展水平。当然,这些发展水平的概念并不是周定个变的,而是随 若研究的目的和时间的改变会相应地变化。发尼水平在文字表达上,常常用“增加到”、“增 训为”,以及“降低到”、“降低为”表示 8.2.2平均发展水平 均发尼水平是不同时期的发展水半的均均数,也称为序时平均数或动态平均数。它与 一般的平均数有相同之处,又存在者明显的区别。相同之处是:子时平均数和一般平均致都 是将现象的个别数量差异抽象化,概括地反映现象的一般水平。两者的区别在于:第一,中 均发展水平是根据动念数列来计算的,从动念上说明同一现象在某一段时内发展的一般水 平:而一般半均数是根据变量数列来计算的,从静态上说明同质总体在一定的时间、地点条 件下的一级水。第 平均发展水平是对同 观象不同时间上的数值差 异的抽家化, 般平均数是对同一时间总体某一数量标志值差异的抽象化,用以反映总体在具体历史条件下 的一般水平,是根据变量数列计算的。 平均发展水平可以山总量指标时向数列计算,也可山相对指标或平均指标的时间数列计 算。其中,山绝对数动念数列计算序时半均数是最基本的方法 想据结 1)时期数列计算序时Ψ均数的计算 ,山于时期数列中的各指标是反映事物的一段时期 内发展过程的结果,其数值可以相加,而月编制时期数列一般要求时期长短相等。因此,计 算方法较为简单,可以采用简单算术半均法,即进期项数除进期数列中各个指标数值之和。 此计算公式为:a=4+4,+A+a_∑g 其中,ā表示序时平均数,a,代表各期发展水半,n代表时期项数。 2)时点数列计算序时平均数的计算。山于资料不同,时点数列有连续时点和向断时点

之分,其计算子时平均数的方法也不同。 日圆 9.1 9.9 9.14 9.25 职工人数 1200 1240 1220 1230 (1)连续时点数列。如果时间数列的资料是按山登记按川排列的,则为连续时点数列。 它又可分为间隔相等和向隔不等两种。 ①间隔相等的连续时点数列。即数列中各时点指标值之间的时间隔相等,都是」, 可用简单算术半均法计算。计算公式为:石=卫 n 例,某企业7月上旬每天的职工人数如表8-6所示。 表8-6某企业职工人数 日期12345678910 职工人数250260240262261263258266272272 a=∑0_250+260+240+262+261+263+258+266+272+272 =260(人) ②间隔不等的连续时点数列。如果被研究对象每隔一段时间才有变动,则用每次变动 持续的时间间隔长度(f)为权数对各时点水平()加权,其计算公式为: a=a+a,++a_∑ 厂+∫+N+厂n ∫ 例,某企业九月份职工人数资料如表8-7所示。 表8-某企业九月份职工人数 ∑4_1200×8+1240x5+1220x1+1230×6=1220人 a- 30 (2)间断时点数列。在实际统计工作中,要统计每一个时点上的数字显然是一项相当 繁杂的工作,为方便起见,通常只能每隔一定的时向间统计一次,时点一般定在期制或期木(如 月初月术、年初年木等),这样每次统计的间隔相等:或者仪当现象的数量发生变动时进行 统计,这样每次统计的间隔就不相等。 ①间隔相等的间断时点数列。它是根据间隔相等的各期期初或期木时点资料编制的时 点数列。此时可以假定相邻两个时点之间的现象变动是均匀的,于是将这两个时点指标数值 相加除以2,即可得到这两个时点之间的序时平均数,再用简单算术平均法求得整个时点数 列的序时平均数 例如某企业2005年第二季度的商品库存额如1表8-8所示 表8-8菜企业2008年第二季度商品库存额 单位:万元 日期 3月 4月 5月 6月 月未炸布额 100 86 104 114 根据表8-8资料,可计算各月和第二季度半均商品库存额:

4月份的¥均库在额=100+86-93万元 5月份的¥均库存额86+10495万元 2 6月份的¥均库存额=104+14=109万元) 则第二手度的¥均库存额=93+95+109=9(万元 上述计算第二季度平均库存额的两个步骤,可以合并简化为: 100+8686+104,104+114 第二季度平均库存额= _93+95+109=99(万元) 3 上面计算过程概括为一般公式 g+0+a,+a+A+0 a=2 2 2 n-1 n-1 式中,ā表示序时平均数 a表示各项时点指标数值: n表示时点个数 根据上述计算公式,间隔相等间断时点数列的序时平均数等于首术项两指标数值之半 加中间各项指标数值,除以时点项数减一,所以称为“首尾折半法”。 ②间隔不等的间断时点数列。它是根据间隔不等的各期期初或期木时点资料编制的时 点数列。同样要假定向断的各时点之间的指标值是均匀变动的,山于各时点之间的向隔不等, 可用各个间隔的长度()为权数,对各相应时点的平均值进行加权平均,求待序时半均数。 计算公式为 +@+0+a5+A+a+af a-- 2 2 2 厂++A+f 例,根据表8-9资料计算2005年某商品的平均库存量 表8-9某商品2008年平均库存 时间1月初3月制 7月初 10月初 12月末 年存量(套) 1500 600 900 1600 1000 根据上表资料,计算某商品2005年的Ψ均库存量为:

1500+600×2+600+900×4+900+1600×3+1600+1000 ×3 =2 2+4+3+3 -=1062.5(套) 根据间断时点数列计算序时半均数,是假定两个相邻时点之间现象数量的变动是均今 的,而实际上各种现象不可能都是均匀变动的,故所得的结果只能是一个近似值。如果时点 数列的间隔越小,则所求得的结果越接近实际。因此,间断时点数列的间隔不宜太长。 2.根据相对数动态数列计算序时平均数 山于相对数动念数列是派生数列,不能用相对指标时向数列的各个指标数值直接相加除 以项数来求得,而要利用其相应的两个绝对数动念数列,分别计算分子数列的序时半均数无 分母数列的序时半均数,而后加以对比,即可求得。其基本计算公式为:。=日 计算时,应先分析对比的分子和分母是时期数列还是时点数列,是哪一种时点数列,然 后再按照前面所述的相应公式计算。具体有三种情形: 1)分子和分母均为时期数列。则有: c=a∑0,∑b∑a ∑b 上式中,需根据所掌握的资料个同采取不同的计算,当所掌握的资料不全时,即 b,c有缺项时,同样可以计算 0c= .a=bc代入上式,得:c= ∑bc 这个公式实际就是加权算述平均数公式。 这个公式实际就是加权调和平均数公式 根据所掌握的实际资料来确定选用哪个公式,三个公式的计算结果应完全相同 例,某企业第一季疫产量计划完成情况如表8-10所示。 表8-10某企业产品第一季度产量完成情况表 时间 一月 _日 实际产(吨 420 714 b计划产量(吨 400 500 700 c计划完成(%) 105 112 102 c= ∑a420+560+714 ∑b 400+500+700 =1.059=105.9% ∑6c_400×105%+500×112%+700x102% =1.059=105.9% ∑b 400+500+700

2004 20052006 200720 a第=产业从业人员数(百人 15456 16851 1790 1837 18679 b全部从业人员数(百人) 67199679476885069600 69957 C第产业从业人员所占比重(%)23.024.826.026.426.7 420+560+714 是0的.+i2%+o2 420.560.714 =1.059=105.9% 2)分子和分母均为时点数列。山于时点数列计算序时半均数,有连续与间断之分,而每 种又有间隔相等和间隔不等之分,这就形成四种不同的情况,但其基本的计算方法不变。现 以最常见的间隔相等间断时点数列对比所形成的相对指标和间隔不 等的间断时点数列对 比所形成的相对指标时间数列序时平均数的计算为例,说明其一般的计算方法。 (1)时间间隔相等间断时点数列。对于该数列,根据前边的基本思路,可采用下公 式: 2 a-a n-1 2+4+n+号 n-1 当所掌程的资料不全时,可将a=bc及b=“代入上式,即可得出两个变形公式为 -g空66+M+g 表8-11菜地区2004一2008年末第三产业从业人员情况表 根据表8-11的资料,某地区2002一2006年间第三产业从业人员数占全部从业人员数的 年平均比重为: 15456+16851+17901+18375+18679 =6799+67947+68850+6960016995725.53% 2 2 若用两个变形公式计算,则: 6719×0.23+67947×0.248+6850x0.26+69600x0.264+69957x0.267 c-2 =25.53% 6719+67947+6850+69600+6957 2 15456+16851+17901+18375+18679 度c=1545616851,17901,1837518679=25.53% 2×0.23+0.248+0.26+0.2642×0.267

(2)时间间隔不等间断时点数列。如果间隔不等,则要用各个间隔长度作权数,用加 权半均法计算分子和分母的序时平均数,然后再对比。其计算公式为: +aj+a+af+A+a+af)÷∑f 2 色+6万+6+6万+A+b+b)+∑f 3)分子和分母为不同性质的时期数列和时点数列。其基本公式不变,仪分子数列和分 母数列的序时平均数的计算方法,应依据数列的具体性质、类别而定。举例如下: 表8-12莱地区208年第三季度各月商品流转次 月 6月 7月 8月 9月 a盛品清传额(万元) 144.0 148.2 154.7 b月末商品存领(万心) 64.2 51.0 47.8 52.0 c商品流转次数 3.1 要求计算该商场第二季度平均商品流转次数和第二季度商品流转次致。 山于商品销售额是时期指标,月木商品年存额是时点指标,故两者个能直接比较,需求 出各月华均商品库存额,能对比求出各月的商品流转次数。计算第一季度月半均商品流封 次数,不能直接将各月的商品流转次数相加平均,而应按照基本公式分别求出分子数列和分 母数列的序时平均数, 再对比求得 d 1440+148.2+154.7 =2.848 言+6+6+ 64.2 52.0 +51.0+47.8+ 13 /(4-1) 计算第三季度商品流转次数,同样也不能将各月的商品流转次数直接加总,它等于第 季度的商品销售总额除以第一季度月平均商品库存额:或等于第一季度的月平均商品流转次 数乘以月数。即: 第三季度商品流转次数 ∑a 144.0+148.2+154.7 =8.544 b 42+51.0+47.8+520 3 或者2.844×3=8.544(次) 3.根据平均数动态数列计算序时平均数 平均指标时间数列可分为一般平均数时向数列和序时半均数时间数列两种 1)山 平均数组成的平均指标时间数列 实际上山是两个总量指标 数列对比形 成的,其方法和山相对数动念数列计算子时平均数的方法基本相同,即分别计算分子数列无 分母数列的序时平均数,然后将这两个序进平均数进行对比,就可求得这两个平均数动态数 列的序时平均数。其中分子是标志总量数列,通常为时期数列,分母是总体单位总数数列, 一般为时点数列,比且体计算方法可参照前例中半均商品流转次数的计算 2)山序时平均数组成的平均指标时间数列计算子时平均数,在时期相等时,可直接采 用简单算术平均法来计算:如时期不相等,则可以时期为权数,采用加权算术平均法计到 例,某商场2005年第二季度各月半均商品库存额表8-12所示。 表8-13某商场2008年第二季度平均各月商品库存额 月份 4月 5月 6月 平均商品存额(万元 57.6 44 49.9
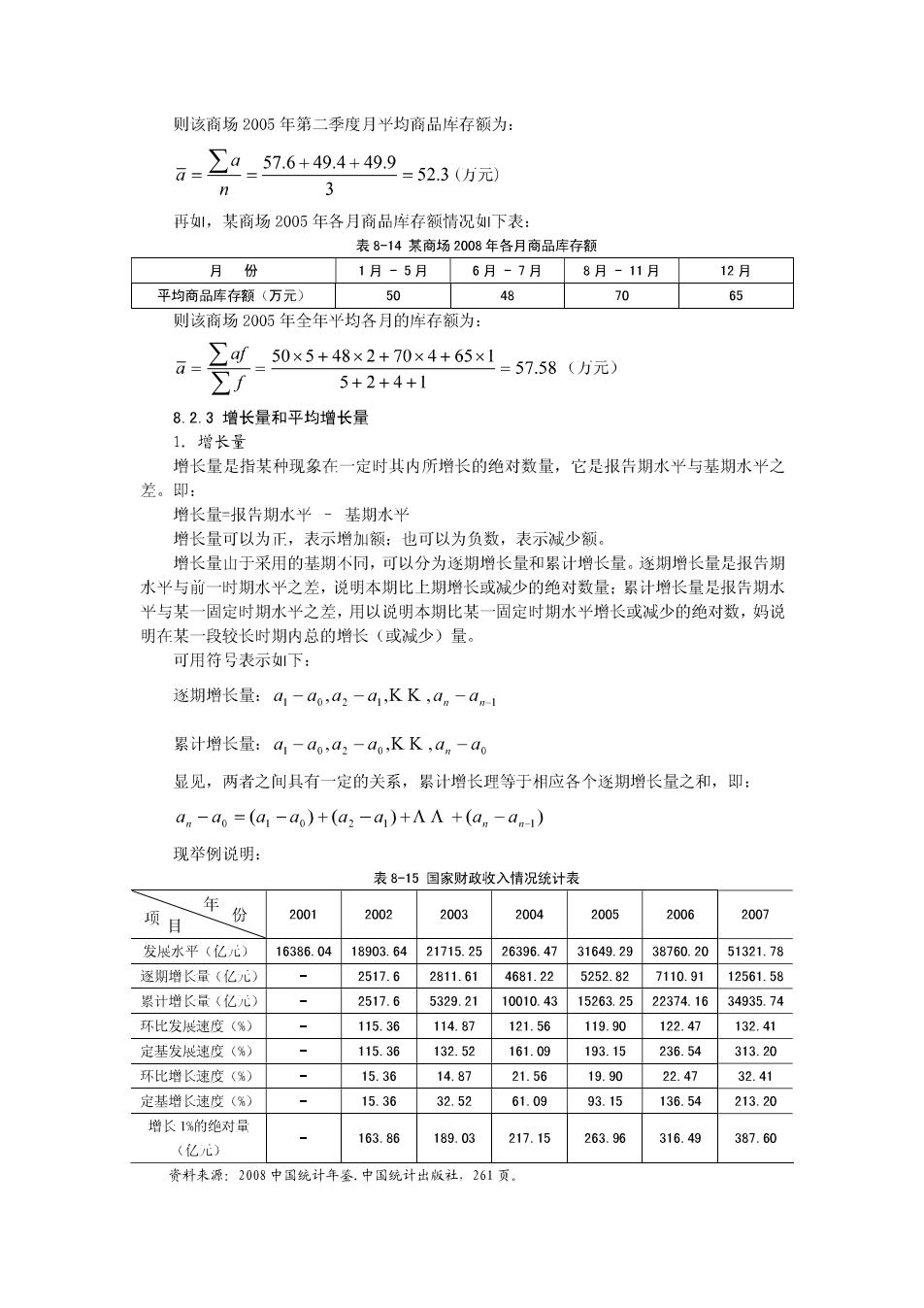
则该商场2005年第二季度月华均商品存额为: 石=2_576+494+499=52305元 3 再如,某商场2005年各月商品库存额情况如下表: 表8-14某商场2008年各月商品库有面 月 1月-5月6月-7月8月-11月 12月 平均商品库存额(万元 50 48 70 65 则该商场2005年全年业均各月的库存额为: ag0x5+4将x2+0x4+651.5758(内元 ∑f 5+2+4+1 82.3增长景和平均增长 1.增长里 增长量是指某种现象在一定时比内所增长的绝对数量,它是报告期水华与基期水华之 差。即: 长量报告期水业一基期水华 增长量可以为正 表示增加额 也可以为负数,表示减少额。 增长量山于采用的基期不同,可以分为逐期增长量和累计增长量。逐期增长量是报告期 水平与前一时期水平之差,说明本期比上期增长或减少的绝对数量:累计增长量是报告期水 平与某一固定时期水平之差,用以说明本期比某一固定时期水平增长或减少的绝对数,妈说 明在某一段较长时期内总的增长(或城少)量 可用符号表示如下: 逐期增长量:a,-ao,a2-a,KK,an-a 累计增长量:a-ao,a2-aKK,a。-a 显见,两者之间具有一定的关系,累计增长理等于相应各个遂期增长量之和,即: a,-ao =(a-ao)+(a;-a )+AA +(a,-a) 现举例说明 表8-15国家财政收入情况统计表 项目 年粉 2001 202 2003 2004 2005 2006 207 发展水平(亿心】 16386.04 18903.64 21715.2 26396.4731649.29 38760.20 51321.78 逐期增长量(亿元)》 2517.6 2811.61 4681.225252.82 7110.91 12561.58 累计增长量(亿元) 25176 532921 10010.4315263.2522374.16 3493574 环比发烘速府 115.36 14.87 121.56 19.90 2247 13241 定基发投速度(% 115.36 132.5 161.09 193.15 236.54 313.20 环比增长速度(%) 15.36 14.87 21.56 19.90 22.47 32.41 定基增长速度(%》 15.36 32.52 61.09 93.15 136.54 213.20 增长1%的绝对司 163.86 189.03 217.15 263.96 316.49 387.60 货来源:2008中国就计年,中国统计出版社,261页