
州题1:配对样本怕数的检验 用简单法和常规法分别对12份人尿进行尿铅 量测定,所得结果如表10-1。问根据现有资 料能否说明两种方法检测结果不同?
用简单法和常规法分别对12份人尿进行尿铅 量测定,所得结果如表10-1。问根据现有资 料能否说明两种方法检测结果不同? 1 例题1:配对样本均数的t检验
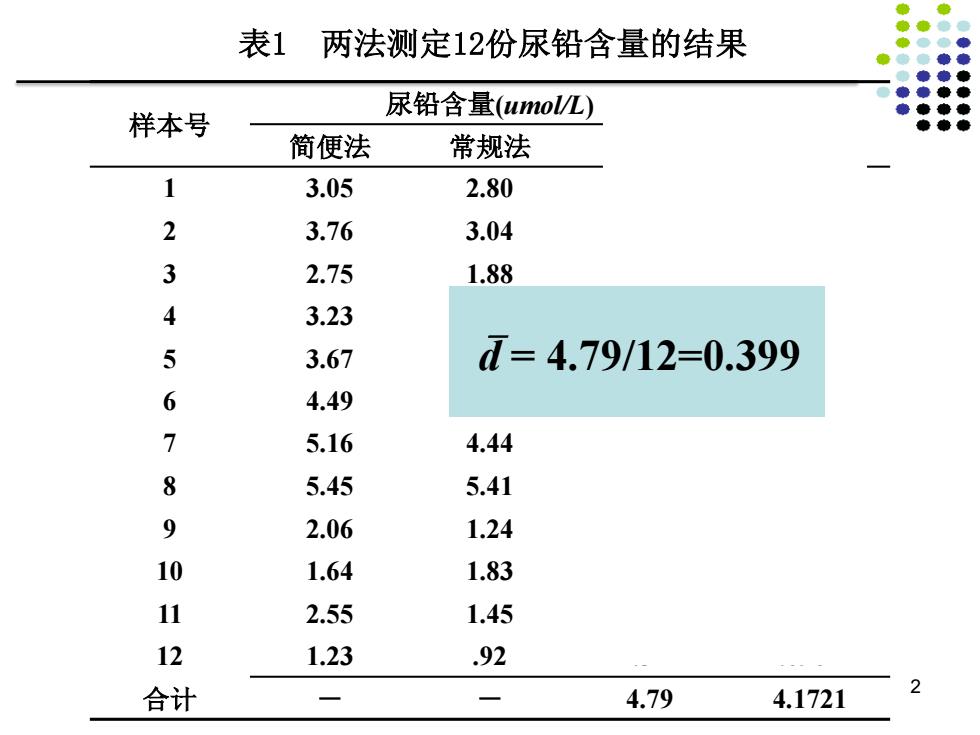
表1两法测定12份尿铅含量的结果 尿铅含量(umol/L) 样本号 简便法 常规法 3.05 2.80 2 3.76 3.04 3 2.75 1.88 4 3.23 5 3.67 d=4.79/12=0.399 6 4.49 7 5.16 4.44 8 5.45 5.41 9 2.06 1.24 10 1.64 1.83 11 2.55 1.45 12 1.23 .92 合计 一 一 4.79 4.1721
样本号 尿铅含量(umol/L) d2 简便法 常规法 差值(d) 1 3.05 2.80 .25 .0625 2 3.76 3.04 .72 .5184 3 2.75 1.88 .87 .7569 4 3.23 3.43 -.20 .0400 5 3.67 3.81 -.14 .0196 6 4.49 4.00 .49 .2401 7 5.16 4.44 .72 .5184 8 5.45 5.41 .04 .0016 9 2.06 1.24 .82 .6724 10 1.64 1.83 -.19 .0361 11 2.55 1.45 1.10 1.2100 12 1.23 .92 .31 .0961 合计 - - 4.79 4.1721 表1 两法测定12份尿铅含量的结果 2 `d = 4.79/12=0.399

配对设计(paired design) ·将两个条件相同或相近的受试对象配成对子, 两个体分别随机接受两种不同的处理 ·同一受试对象的两个部分配成对子,分别随机 接受两种不同的处理 。同一受试对象接受两种不同的处理 自身前后配对,即将同一受试对象,接受某种 处理之前和接受该处理之后视为配对
3 配对设计(paired design) l 将两个条件相同或相近的受试对象配成对子, 两个体分别随机接受两种不同的处理 l 同一受试对象的两个部分配成对子,分别随机 接受两种不同的处理 l 同一受试对象接受两种不同的处理 l 自身前后配对,即将同一受试对象,接受某种 处理之前和接受该处理之后视为配对

配对设计的应用 对子编号 11 3 4 6 动物编号 1.11.212.12.213.13.24.14.21515.216.16.27.1 7.2 随机数 57 3512733!7224!5363194 09141 10176 47 序号 2 11 2 2 1 组别 B A B B B B A
4 配对设计的应用

计算统计重 计算出各对子差值d的均数d,当比较住 效果相同时,d的总体均数4,=O, 故可将配对设计资料的假设检验观为: 样本均数d与总体均数a=O的比较, 所用方法一一配对检险 d-= d t= U=n-1 Sa Saln S.-y ∑d-(∑d2/n n-1 5
1 ( ) / , 1 / 2 2 - - = = = - - = å å n d d n S n S n d S d t d d d d u µ 0 d 0 d d d t d d µ µ = = 计算出各对子差值 的均数 ,当比较组间 效果相同时, 的总体均数 , 故可将配对设计资料的假设检验视 样本均数 与总体均数 的比较 为: , 所用方法--配对 检验 5 计算统计量

例题2:配对样本怕教的检骏 ● 1.建立假设,确定显著性水平 H,4=0(两种方法测定的结果相同) H:40(两种方法测定的结果不同) a=0.05(双侧检验) 2.计算统计量 4.1721-4.792/12 Sa= ∑d-(∑d1n =0.453 n-1 12-1 d-d 0.399 t三 =3.051,w=11 Sa S,/Vn0.453/√12 6
1. 建立假设,确定显著性水平 H0: µd=0 (两种方法测定的结果相同) H1: µd≠0 (两种方法测定的结果不同) a = 0.05(双侧检验) 2. 计算统计量 2 2 2 ( )/ 4.1721 4.79 /12 0.453 1 12 1 0.399 3.051, 11 / 0.453/ 12 d d d d d dn S n d d t S S n µ u - - === - - - == = = = å å 6 例题2:配对样本均数的t检验
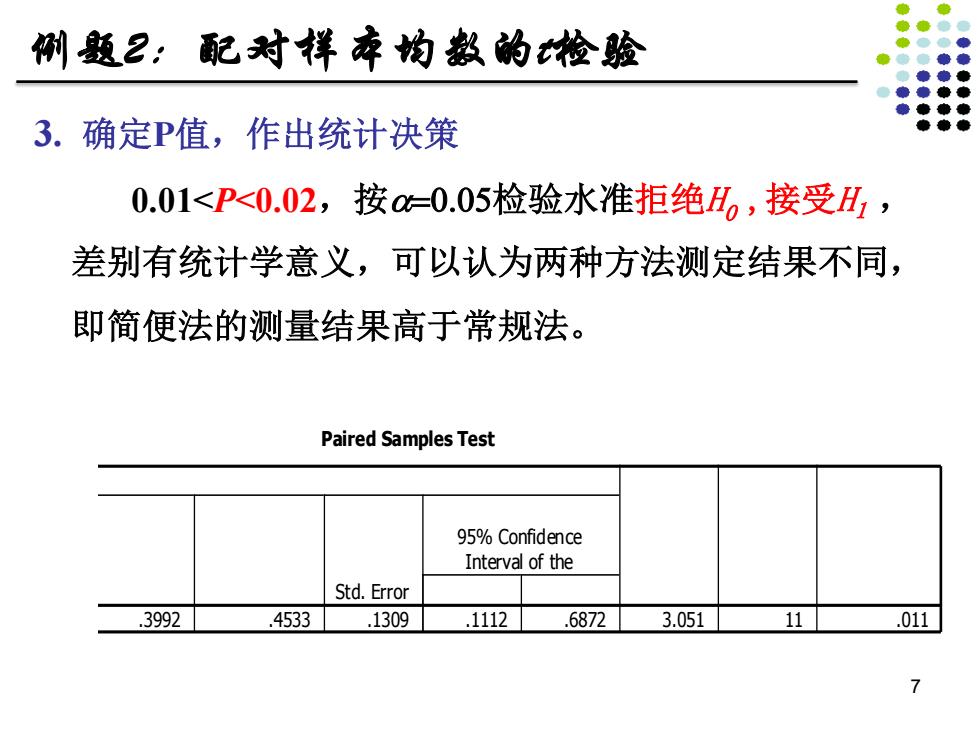
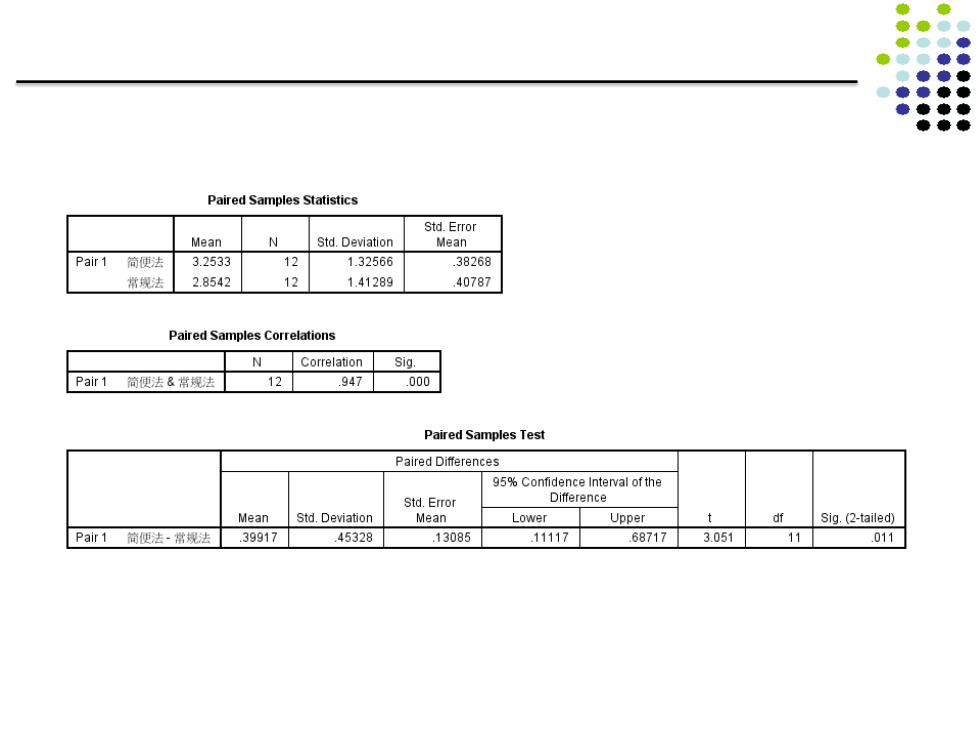
俐题2:配对样本怕教的检验 3.确定P值,作出统计决策 0.01<P<0.02,按o=0.05检验水准拒绝H2,接受H1, 差别有统计学意义,可以认为两种方法测定结果不同, 即简便法的测量结果高于常规法。 Paired Samples Test 95%Confidence Interval of the Std.Error 3992 4533 .1309 .1112 .6872 3.051 11 .011 7
3. 确定P值,作出统计决策 0.01<P<0.02,按a=0.05检验水准拒绝H0 ,接受H1 , 差别有统计学意义,可以认为两种方法测定结果不同, 即简便法的测量结果高于常规法。 Paired Samples Test Pair 1 SIMPLE - CONVT Mean .3992 Std. Deviation .4533 .1309 .1112 .6872 3.051 11 .011 Std. Error Mean Lower Upper 95% Confidence Interval of the Difference Paired Differences t df Sig. (2-tailed) 7 例题2:配对样本均数的t检验

文件⑤编辑E)视图心数据D)文件旧编辑E)视图心数据D)转换D分析A)直销M图形 名称 分析A直销M图形(G)实用程序U窗口W帮助 1 简便法 简便法 常规法 报告 2 常规法 1 3.05 2. 描述统计 A 3 2 3.76 3 表(T 比较均值仙 圆均值随 3 2.75 一般线性祺型(G) 国单样本T检验⑤) 广义线性棋型 4 3.23 3. 图独立样本I检验D 混合棋型3 盟配对样本T检验巴) 5 3.67 3. 相关(C) 国单因素ANOVA. 回均R) 6 4.49 4.00 7 5.16 4.44 8 自配对样本T检验 9 成对变量 选项0). 10 令简便法 对A) Variable1 Variable2 常规法 7 简便法】常规法灯 Bootstrap(B) 11 12 1.23
Paired Samples Statistics Std.Error Mean N Std.Deviation Mean Pair 1 简便法 3.2533 12 1.32566 .38268 常规法 2.8542 12 1.41289 40787 Paired Samples Correlations N Correlation Sig. Pair 1 简便法&常规法 12 .947 .000 Paired Samples Test Paired Differences 95%Confidence Interval of the Std.Error Difference Mean Std.Deviation Mean Lower Upper df Sig.(2-tailed) Pair 1 简便法·常规法 .39917 45328 .13085 11117 68717 3.051 11 011