
回归与相关 regression correlation
回归与相关 regression & correlation 1

例题 ● 某医师测量了15名正常成年人的体重(kg) 与CT双肾总体积l)大小,数据如下, 据此回答两变量是否有关联? 其方向和密切程度如何 2
某医师测量了15名正常成年人的体重(kg) 与CT双肾总体积(ml)大小,数据如下, 据此回答两变量是否有关联? 其方向和密切程度如何 例题 2
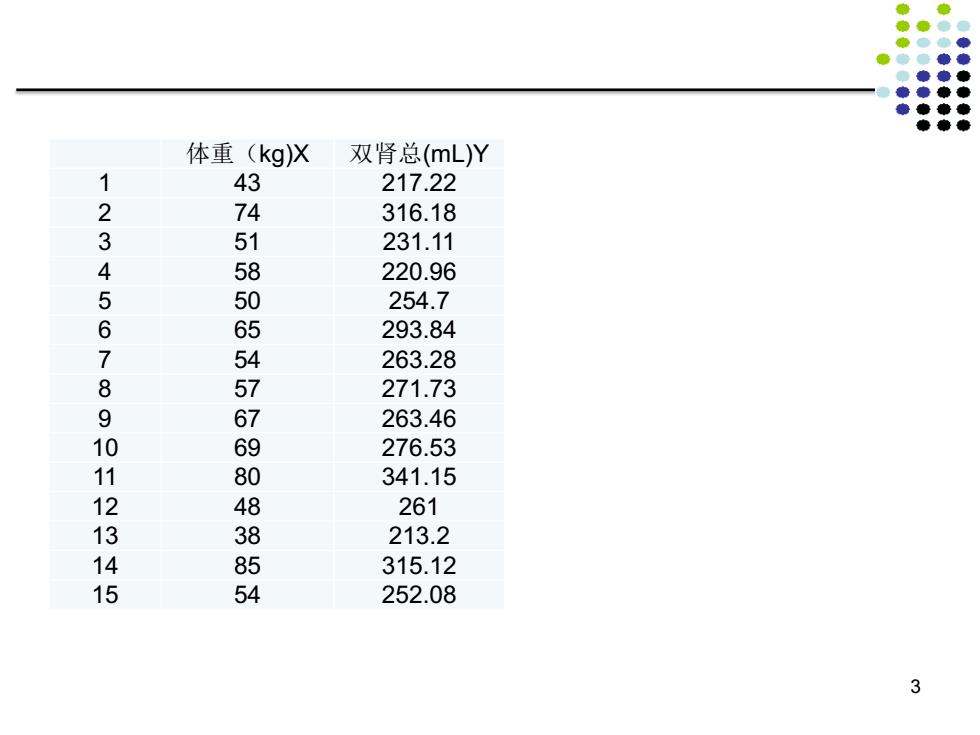
体重(kg)X 双肾总(mL)Y 1 43 217.22 234 74 316.18 51 231.11 58 220.96 50 254.7 56789 65 293.84 54 263.28 57 271.73 67 263.46 69 276.53 80 341.15 48 261 38 213.2 14 85 315.12 1 54 252.08 3
3 体重(kg)X 双肾总(mL)Y 1 43 217.22 2 74 316.18 3 51 231.11 4 58 220.96 5 50 254.7 6 65 293.84 7 54 263.28 8 57 271.73 9 67 263.46 10 69 276.53 11 80 341.15 12 48 261 13 38 213.2 14 85 315.12 15 54 252.08
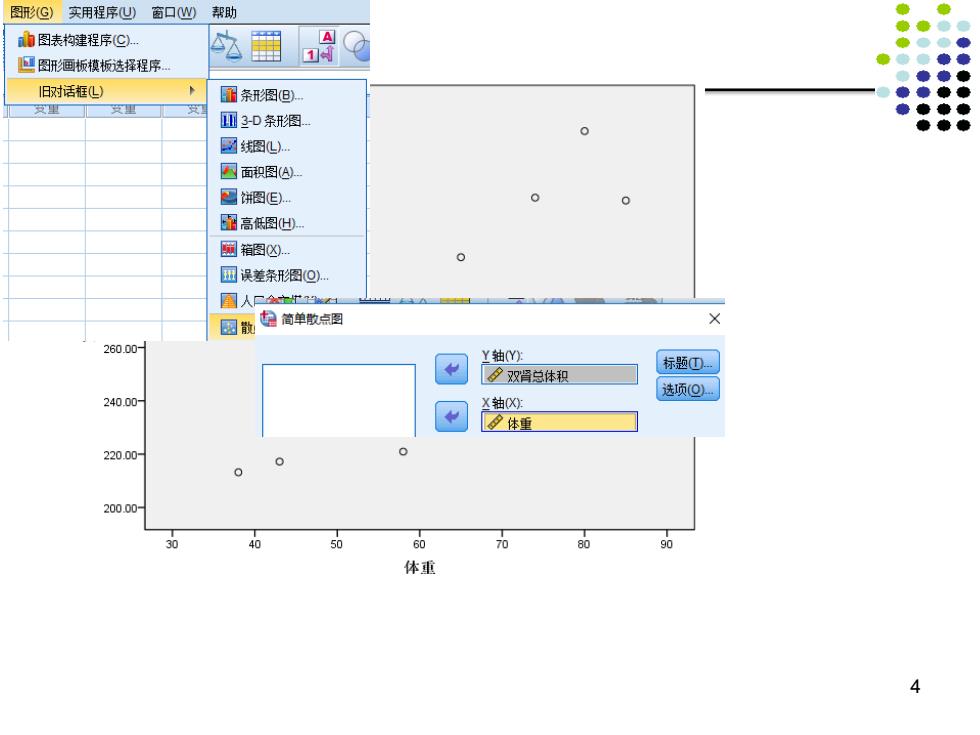
图(G)实用程序U)窗口W帮助 山图表构建程序C) 国图形画板模板透择程序 A ●● 旧对话框L) 团条形图⑧) ● 文里 ◆ ●· Ⅲ3-D条形图 圖心 面积图(A) □饼图但) 图高图H 国箱图公 0 国误差条形恩Q) 国人P☆r2 图散自简单散卓图 × 260.00 Y轴Y 标题①。 夕双肾总体积 选项(O) 240.00 X轴X) 体重 220.00 0 200.00 30 40 50 60 70 80 90 体重 4
4
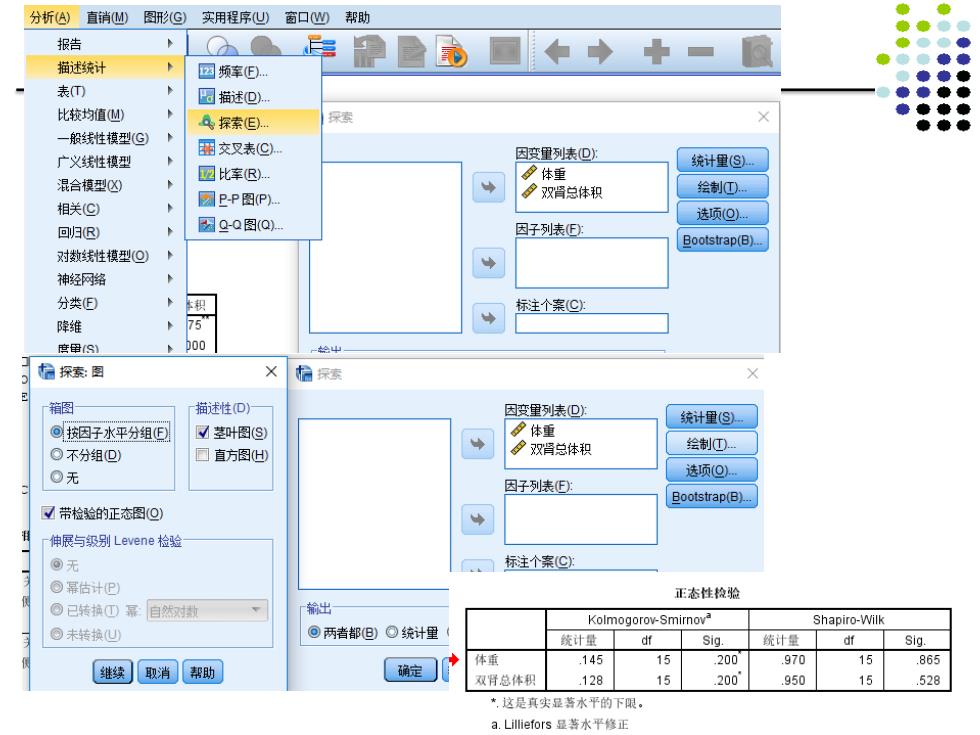
分析A)直销M图形G 实用程序心) 窗口帮助 报告 A h 描述统计 A 回频车) 表(T 国描述迎 比较均值M) 4探索但). 一般线性模型(©) 国交叉表(C 广义线性模型 因变里列表(D月 统计里(S) 四比幸R) 令体重 混合模型☒) 绘制① P-P图(P) 号双肾总体积 相关(©) A 选项(O) 回归R) 因-Q图(Q) 因子列表( Bootstrap(B). 对数线性模型(O) 神经网路 分类日 积 标注个案(C】 降维 75 度留S1 D00 中 5 探索:图 拾探索 箱图 描述性D) 因变里列表巴少 统计里(S). ⊙按因子水平分组(E ☑茎叶图(S) 号体重 ⊙不分组D) 口直方阁山 双肾总体积 绘制① ⊙无 选项(O) 因子列表: Bootstrap(B) ☑带检验的正态图(O) 伸展与级别Levene检验 @无 标注个案(C) ©幂估计P 正态性检验 ©已转换①幂自然封 输出 Kolmogorov-Smirnova Shapiro-Wilk ©未转换U ⊙两者都)○统计里 统计量d州 Sig. 统计量dSig. 体重 .145 15 .200 .970 15 继续取消 中 确定 ,865 帮助 双肾总体积 128 15 200 950 15 528 *,这是真实显著水平的下限。 a.Lilliefors显菩水平修正
5
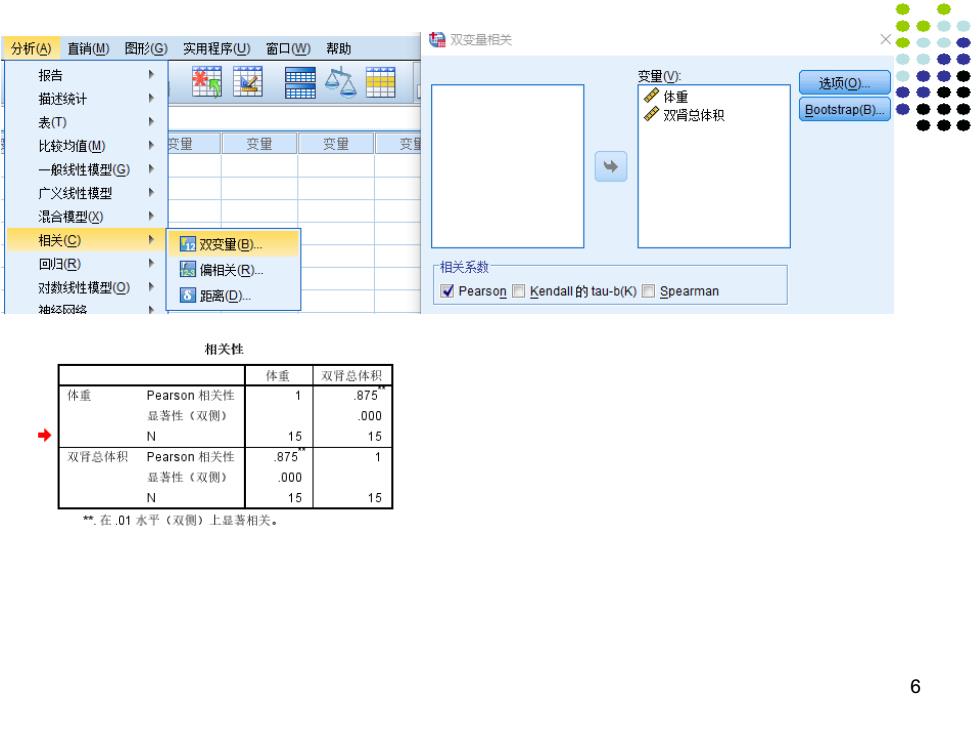
分析(A)直销M)图形G)实用程序U窗口凹帮助 月双变量相关 海 报告 画%国 变里心: 选项(O) ◆ 描述统计 体重 表m 分双肾总体积 旦ootstrap(B)- ◆ 比较均值山 变里 变里 变里 变里 一般线性模型(G】 广义线性模型 混含模型C) 相关(C 团双变里但 回归R) 圆偏相关 相关系数 对数线性模型⊙ 8距离D)以 Pearson□Kendall的tau-b(K□Spearman 袖坏网绘 相关性 体重 双肾总体积 体重 Pearson相关性 1 .875 显菩性(双侧) 000 N 15 15 双肾总体积Pearson相关性 .8751 显著性(双侧) .000 N 15 15 在.01水平(双侧)上显著相关。 6
6

线性相关(linear correlation) 前提假设:(X,)服从正态分布, 即适用于双变量正态分布资料 研究目的:分析两个变量之间有无相关关系 相关系数:(linear correlation coefficient) 描述两变量间线性相关的密切程度 和相关方向的统计量
线性相关(linear correlation) 前ᨀ假设:(X, Y)服从正态分布, 即适用于双变量正态分布资料 研究目的:分析两个变量之间有无相关关系 相关系数: (linear correlation coefficient) ᧿述两变量间线性相关的密切程度 和相关方向的统计量 7
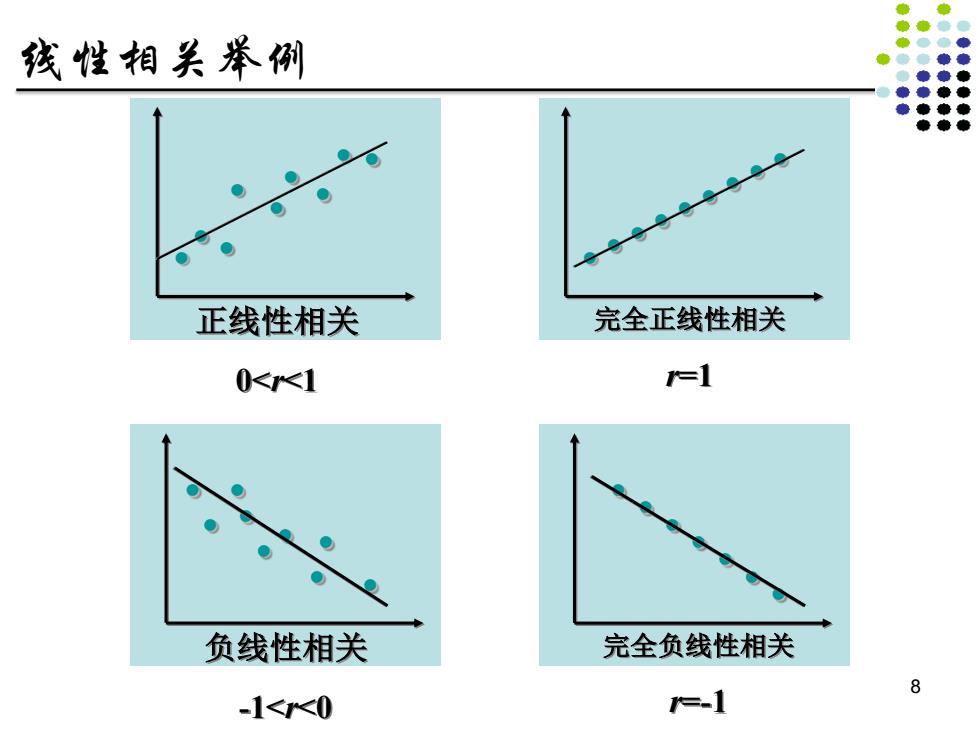
线性相关举例 正线性相关 完全正线性相关 0<K1 =1 负线性相关 完全负线性相关 8 -1<K0 =-1
负线性相关 -1<r<0 正线性相关 0<r<1 完全负线性相关 r=-1 完全正线性相关 r=1 线性相关举例 8����������������������������������
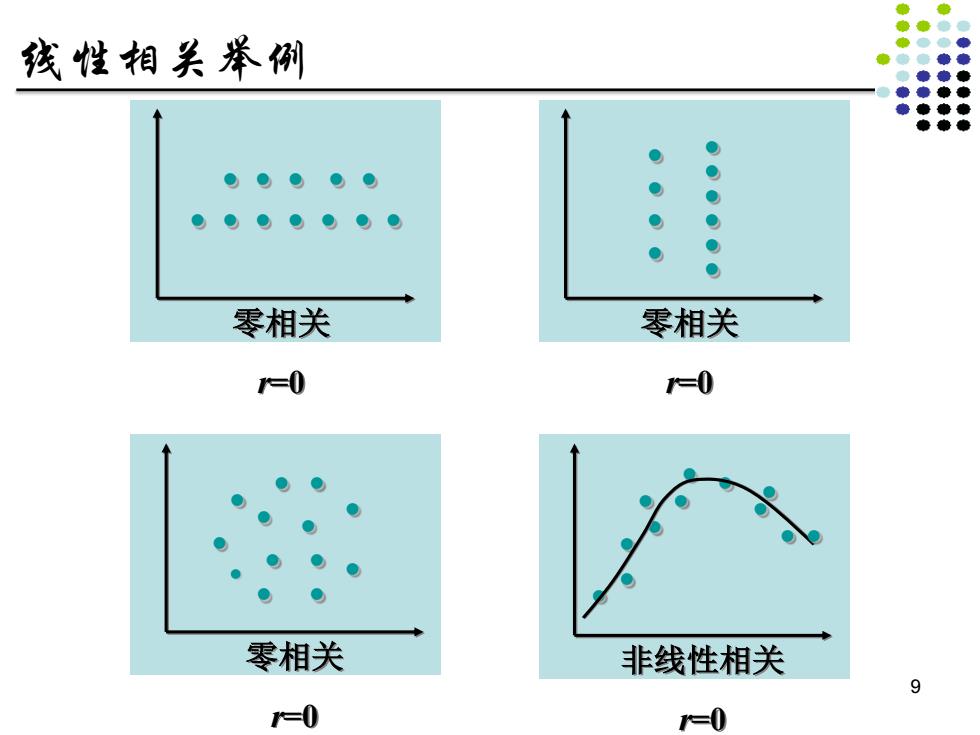
线性相关举例 ● ● ● ● 零相关 零相关 =0 =0 零相关 非线性相关 9 =0 =0
非线性相关 r=0 零相关 r=0 零相关 r=0 零相关 r=0 线性相关举例 9�����������������������������������������������

线性相关系数 又称:积差相关系数(coefficient of product-moment correlation)/Pearson相关系数/相关系数 样本相关系数:r -1≤s1 总体相关系数:p r越大,线性 相关越密切 ∑(X-X)Y-) 1x √∑(X-XΣ(Y-Vadm 10
又称:积差相关系数(coefficient of product-moment correlation) / Pearson相关系数 / 相关系数 样本相关系数:r 总体相关系数:r 2 2 ( )( ) ( )( ) XY XX YY X XY Y l r X X YY l l - - = = - - å å å -1≤ r≤1 |r|越大,线性 相关越密切 线性相关系数 10