
秩和检验适用的资料特点 >半定量资料即等级资料 >偏态分布 >资料分布类型不明确 >个别数据偏离过大或数据某一端的值不确定 >各组离散程度相差悬殊 1
Ø 半定量资料即等级资料 Ø 偏态分布 Ø 资料分布类型不明确 Ø 个别数据偏离过大或数据某一端的值不确定 Ø 各组离散程度相差悬殊 1 秩和检验适用的资料特点
秩和检验(rank sum test) 秩号:将各原始数据从小到大排列,分别给每个数 据一个顺序号,也就是秩号(rank)。 如: 7.5 13 秩号: 3 1 2 4 秩和:秩号的和 秩和检验:用各组秩和代替原始数据进行假设检验。 较小例数组的秩和,n,≠n2 T= min(R,R2),n=n 2
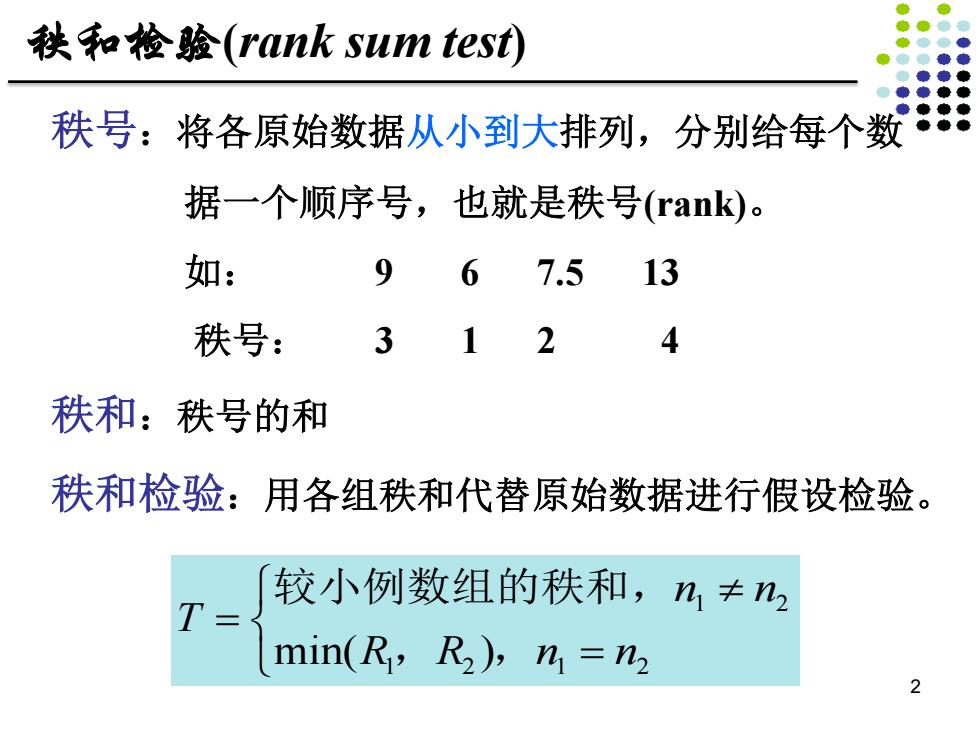
秩号:将各原始数据从小到大排列,分别给每个数 据一个顺序号,也就是秩号(rank)。 如: 9 6 7.5 13 秩号: 3 1 2 4 秩和:秩号的和 秩和检验:用各组秩和代替原始数据进行假设检验。 1 2 min( ) 12 1 2 n n T RR n n ì ¹ = í î = 较小例数组的秩和, , , 2 秩和检验(rank sum test)

配对役计资料的秩和检验 适用于:配对设计资料,差数严重偏离正态 分布,但差数的总体分布对称。 方法:符号秩和检验(signed rank test) 3
适用于:配对设计资料,差数严重偏离正态 分布,但差数的总体分布对称。 方 法:符号秩和检验(signed rank test) 3 配对设计资料的秩和检验

例题2 采用配对设计,用某种放射线的A、B两种方式 局部照射家兔的两个部位,观察放射性急性皮 肤损伤程度,见表3。用符号秩和检验比较A、 B两种方式的损伤程度是否不同。 4
采用配对设计,用某种放射线的A、B两种方式 局部照射家兔的两个部位,观察放射性急性皮 肤损伤程度,见表3。用符号秩和检验比较A、 B两种方式的损伤程度是否不同。 4 例题2
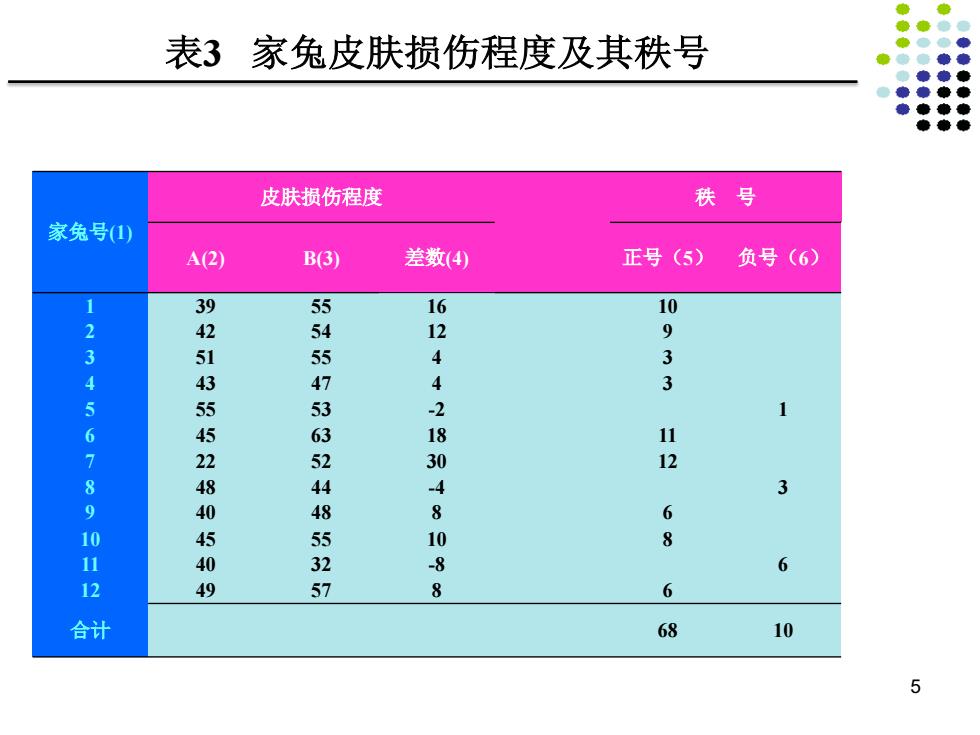
表3家兔皮肤损伤程度及其秩号 ● 皮肤损伤程度 秩号 家兔号(1) A(2) B3) 差数(4 正号(5) 负号(6) 39 5 16 10 2 12 3 55 4 3 4 6 7 9 10 215551280509 4 53 -2 63 18 11 52 30 12 44 -4 3 6 5 10 11 6 12 必 8 6 合计 68 10 5
表3 家兔皮肤损伤程度及其秩号 5 家兔号(1) 皮肤损伤程度 秩 号 A(2) B(3) 差数(4) 正号(5) 负号(6) 1 39 55 16 10 2 42 54 12 9 3 51 55 4 3 4 43 47 4 3 5 55 53 -2 1 6 45 63 18 11 7 22 52 30 12 8 48 44 -4 3 9 40 48 8 6 10 45 55 10 8 11 40 32 -8 6 12 49 57 8 6 合计 68 10

1.建立检验假设,确定检验水准 H0:两处理效应相同 H:两处理效应不同 0=0.05 6
1. 建立检验假设,确定检验水准 H0:两处理效应相同 H1:两处理效应不同 a=0.05 6

2.编秩: ① 差数为0的数据忽略不计; ② 余下的个差数按绝对值由小到大排秩号, 排好后秩号要保持原差数的符号; ③ 差数绝对值相等时,求平均秩号表示; 求秩和:即将正负秩号分别相加 R=68,R=10 检验统计量:R=10(较小的一个秩和) 7
2. 编秩: ① 差数为0的数据忽略不计; ② 余下的n个差数按绝对值由小到大排秩号, 排好后秩号要保持原差数的符号; ③ 差数绝对值相等时,求平均秩号表示; 求秩和: 即将正负秩号分别相加 R+=68,R-=10 检验统计量: R=10 (较小的一个秩和) 7

3.确定P值,下结论 查附表11,P<0.05,在o=0.05水准上拒绝Ho, 接受H1,即认为A、B两种照射方式造成的急性 皮肤损伤程度不同。 8
3.确定P值,下结论 查附表11 ,P<0.05,在a=0.05水准上拒绝H0, 接受H1,即认为A、B两种照射方式造成的急性 皮肤损伤程度不同。 8

当>10时,统计量R作变换后近 似服从标准正态分布 (n+)/4-R W= n是对子数 Vn(n+1)(2n+1)/24 本例,u= 12(12+1)/4-10 =2.275 V12(12+1)(2×12+1)/24 1.96≤u≤2.58,故0.05>P>0.01, 在o=0.05水准上拒绝H,接受H。 9
当n>10时,统计量R作变换后近 似服从标准正态分布 ( 1) / 4 | | ( 1)(2 1) / 24 nn R u n nn n + - = + + , 是对子数 0 12(12 1) / 4 |10 | 2.275 12(12 1)(2 12 1) / 24 1.96 2.58 0.05 0. . 05 P 0 01 u H H u a + - = = + ´ > + 1 本例, ,故 , 在 = 水准上拒绝 ,接受 。 9

若存在多个差数的绝对值相等,即 有相同的秩号:校正 n(n+1)/4-R u= Vn+102n+1)/24-∑(E-t)/48 本例,u=2.282 1.96P>0.01, 在a=0.05水准上拒绝Ho,接受H。 10
若存在多个差数的绝对值相等,即 有相同的秩号:校正 ( ) ( 1) / 4 | | ( 1)(2 1) / 24 / 48 i nn R u nn n t t + - = + + - - å 3 i 0 1 2.282 1.96 2.58 0.05 0.05 0.01 P u H H u a > = 本例, ,故 , 在 = 水准上拒绝 ,接受 。 10