
应用条件 在四格表资料中,当出现下列情况之一时, 应选用四格表的确切概率法。 。1.n<40 ·2.有理论频数≤1 ·3.用其它检验方法所得P接近α
应用条件 在四格表资料中,当出现下列情况之一时, 应选用四格表的确切概率法。 • 1.n<40 • 2.有理论频数≤1 • 3.用其它检验方法所得P 接近α 1

基本思想 四格表确切概率的基本思想是:在四格表的周边 合计不变的条件下,用公式 P=(a+b)!(c+d)!(a+c)!(bd)! a!b!cld!n! 直接计算表内四个数据的各种组合之概率。 2
基本思想 • 四格表确切概率的基本思想是:在四格表的周边 合计不变的条件下,用公式 直接计算表内四个数据的各种组合之概率。 2 ! ! ! ! ! ( )!( )!( )!( )! a b c d n a b c d a c b d Pi + + + + =

计算公式 Ps (a+b)(c+d)!(a+c)(b+d)! a!b!cld!n! 式中a、b、c、d和n的意义同前, !为阶乘符号。0!=1, 1!=1,3!=3×2×1=6
计算公式 ! ! ! ! ! ( )!( )!( )!( )! a b c d n a b c d a c b d P + + + + = 式中a、b、c、d 和n的意义同前 , !为阶乘符号。0!= 1, 1!= 1 ,3!= 3×2×1 = 6

求P值的步骤 ·列四格表。使四格表周边合计数不变, 依次增减四格表中任一格子的数据,列 出所有可能的四格表。 ·列四表格的数量=最小合计数+1
求P值的步骤 • 列四格表。使四格表周边合计数不变, 依次增减四格表中任一格子的数据,列 出所有可能的四格表。 • 列四表格的数量=最小合计数+1
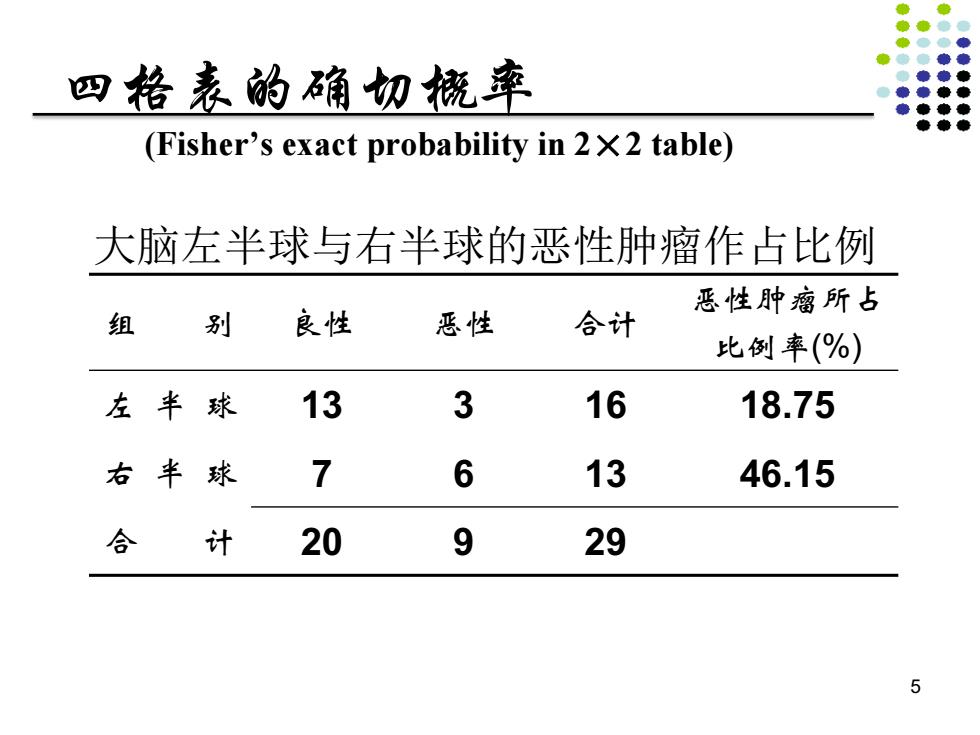
四格表的确切概率 (Fisher's exact probability in 2X2 table) 大脑左半球与右半球的恶性肿瘤作占比例 恶性肿瘤所占 组 别 良性 恶性 合计 比例率(%) 左半球 13 3 16 18.75 右半球 7 6 13 46.15 合 计20 9 29 5
四格表的确切概率 (Fisher’s exact probability in 2×2 table) 大脑左半球与右半球的恶性肿瘤作占比例 组 别 良性 恶性 合计 恶性肿瘤所占 比例率(%) 左 半 球 13 3 16 18.75 右 半 球 7 6 13 46.15 合 计 20 9 29 5
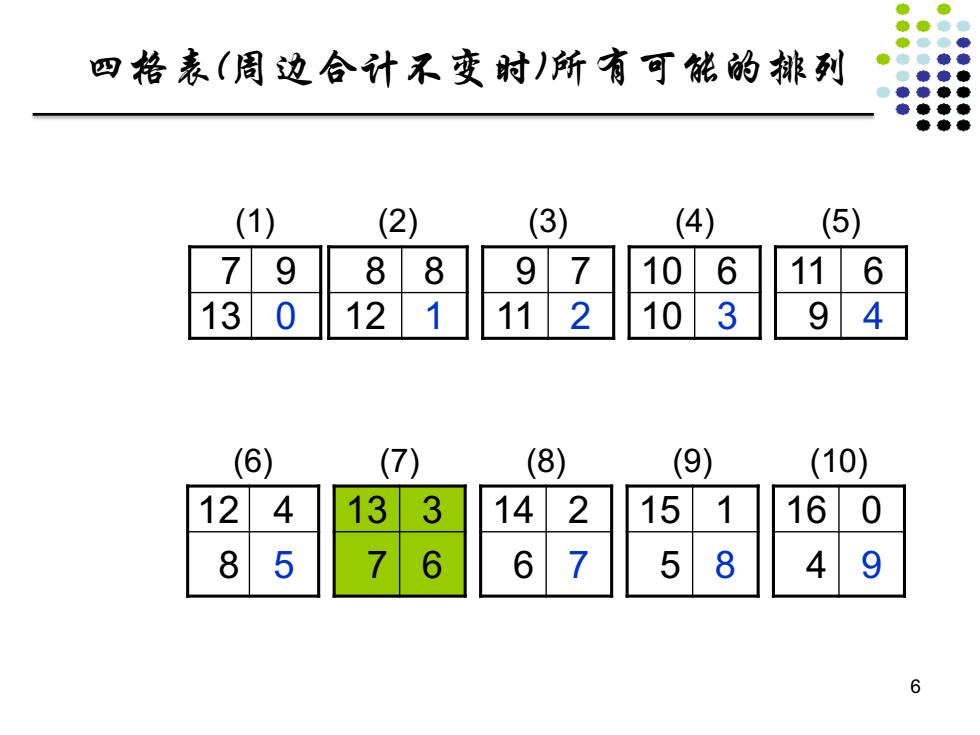
四格表(周边合计不变时)所有可能的排列 (1) (2) (3) (4) (5) 79 8 8 9 7 10 6 116 13 0 12 1 112 10 3 9 4 (6) (7) (8) (9) (10) 12 4 13 3 14 2 15 1 16 0 8 5 6 6 7 5 8 4 9 6
四格表(周边合计不变时)所有可能的排列 (1) (2) (3) (4) (5) 7 9 8 8 9 7 10 6 11 6 13 0 12 1 11 2 10 3 9 4 (6) (7) (8) (9) (10) 12 4 13 3 14 2 15 1 16 0 8 5 7 6 6 7 5 8 4 9 6

超儿何分布 。 超几何分布是统计学上一种离散概率分布。它描 述了由有限个物件中抽出个物件,成功抽出指定 种类的物件的次数(不归还)。 例如在有N个样本,其中个是不及格的。超几何分布描述了在该N个样本中抽出个,其中k个是无效的的概 率 f(k;N,m,n)= N 上式可如此理解: ()表示所有在N个样本中抽出个的方法数目。(风)表示在m个样本中,抽出k个的方法数 目。剩下来的样本都是及格的,而及格的样本有Nm个,剩下的抽法便有(W二?种
超几何分布 • 超几何分布是统计学上一种离散概率分布。它描 述了由有限个物件中抽出n个物件,成功抽出指定 种类的物件的次数(不归还)。 7
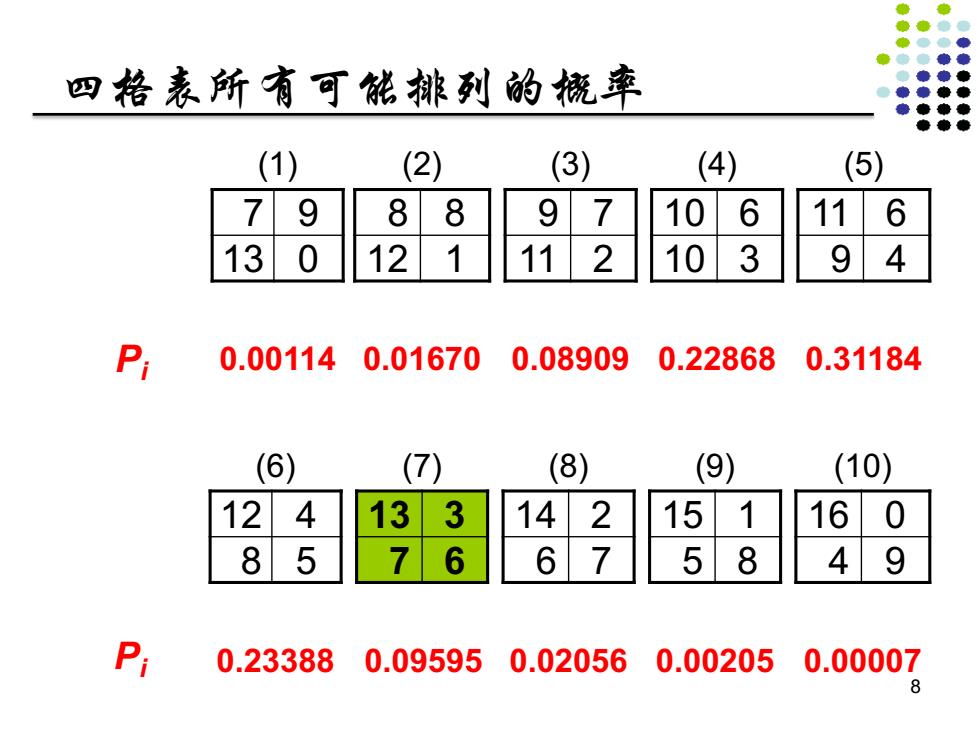
● 四格表所有可能排列的梳率 (1) (2) (3) (4) (5) 7 9 88 9 7 10 6 11 6 13 0 12 1 112 10 3 9 4 P 0.001140.01670 0.089090.228680.31184 (6) (8) (9) (10) 12 4 3 14 15 1 16 0 8 5 6 6 5 8 4 9 P 0.233880.095950.020560.002050.00007 8
四格表所有可能排列的概率 (1) (2) (3) (4) (5) 7 9 8 8 9 7 10 6 11 6 13 0 12 1 11 2 10 3 9 4 Pi 0.00114 0.01670 0.08909 0.22868 0.31184 (6) (7) (8) (9) (10) 12 4 13 3 14 2 15 1 16 0 8 5 7 6 6 7 5 8 4 9 Pi 0.23388 0.09595 0.02056 0.00205 0.00007 8
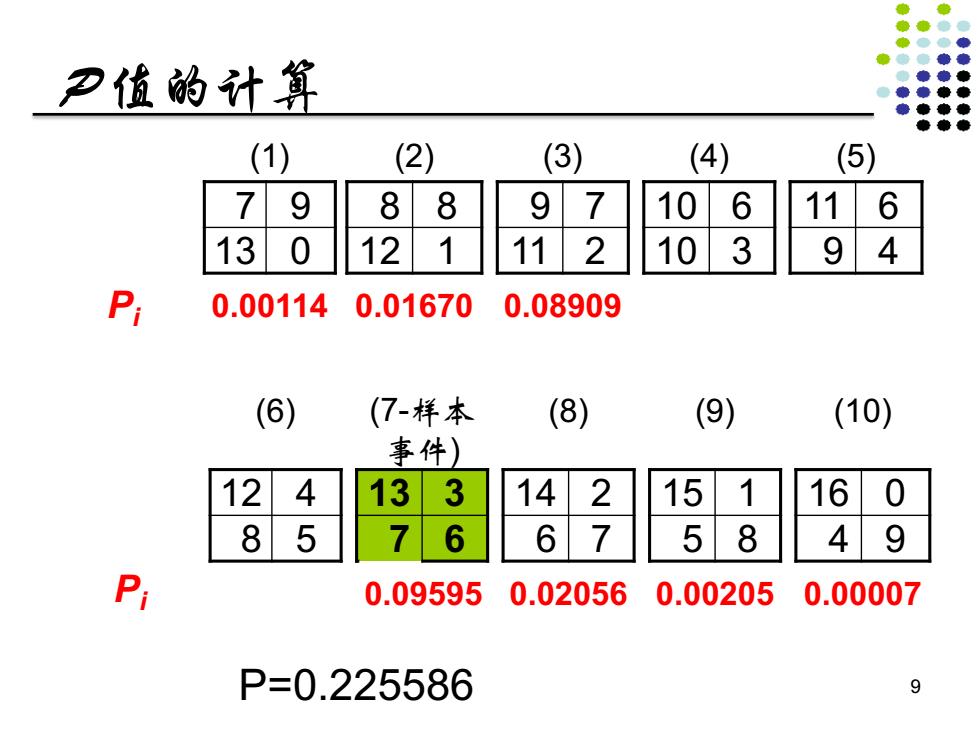
P值的计算 (1) (2) (3) (4) (5) 7 9 8 8 9 7 10 6 116 13 0 12 1 11 2 10 3 94 P 0.00114 0.01670 0.08909 (6) (7-样本 (8) (9) (10) 事件) 12 4 13 3 14 2 15 1 16 0 8 5 7 6 6 7 5 8 4 9 0.095950.02056 0.00205 0.00007 P=0.225586 9
P 值的计算 (1) (2) (3) (4) (5) 7 9 8 8 9 7 10 6 11 6 13 0 12 1 11 2 10 3 9 4 Pi 0.00114 0.01670 0.08909 (6) (7-样本 事件) (8) (9) (10) 12 4 13 3 14 2 15 1 16 0 8 5 7 6 6 7 5 8 4 9 Pi 0.09595 0.02056 0.00205 0.00007 P=0.225586 9

结论 1.建立检验假设,确定显著性水平 :兀1=元2 H:兀1≠T2 0=0.05。 2.计算概率值P=0.226 按a=0.05水准,不拒绝H0,差异没有统计 学意义。故尚不能认为大脑两半球恶性 肿瘤所占比例有差别。 10
结 论 1. 建立检验假设,确定显著性水平 H0:p1= p2 H1:p1¹ p2 a=0.05。 2. 计算概率值 P=0.226 按a=0.05水准,不拒绝H0 ,差异没有统计 学意义。故尚不能认为大脑两半球恶性 肿瘤所占比例有差别。 10