
引例1: 随机抽取一些常年锻炼的成年男子,测其脉搏数,推 断他们的平均脉搏数X与一般正常成年男子脉搏数4是否 有差别,以说明锻炼对成年男子脉搏数的影响。 问题转化为: 由抽样结果判断假设u=是否成立?
引例1: 随机抽取一些常年锻炼的成年男子,测其脉搏数,推 断他们的平均脉搏数�"与一般正常成年男子脉搏数µ0是否 有差别,以说明锻炼对成年男子脉搏数的影响。 问题转化为: 由抽样结果判断假设� = �"是否成立?

引例2: 将一批白鼠随机分为两组,分别喂不同饲料,一段时 间后记录体重增加值,得到两样本均数X、X,推断喂不 同饲料的白鼠平均体重增加值41、,2是否有差别,以说明 不同饲料对白鼠体重增加值的影响。 问题转化为: 由抽样结果判断假设u1=2是否成立?
引例2: 将一批白鼠随机分为两组,分别喂不同饲料,一段时 间后记录体重增加值,得到两样本均数�%、�&,推断喂不 同饲料的白鼠平均体重增加值�%、�&是否有差别,以说明 不同饲料对白鼠体重增加值的影响。 问题转化为: 由抽样结果判断假设�% = �&是否成立?

假设检验: 事先对总体特征做出某种假设,通过分析样本信 息,判断该样本信息是否支持这种假设,从而作出拒 绝或不拒绝这种假设的取舍抉择。又称显著性检验 (significance test). 根据样本的信息检验关于总体的某个假设是否正确
假设检验: 事先对总体特征做出某种假设,通过分析样本信 息,判断该样本信息是否支持这种假设,从而作出拒 绝或不拒绝这种假设的取舍抉择。又称显著性检验 (significance test)。 根据样本的信息检验关于总体的某个假设是否正确

一般新生儿 矿区新生儿55人 头围均数:34.50cm 头围均数:33.89cm 标准差:1.99cm 试问: 该矿区新生儿的头围总体均数与一般新 生儿头围总体均数是否不同?
头围均数:34.50cm 标准差:1.99cm 一般新生儿 矿区新生儿55人 头围均数:33.89cm 试问: 该矿区新生儿的头围总体均数与一般新 生儿头围总体均数是否不同?

案例中 : 假设(检验假设H,),:矿区新生儿头围的总体均数符号为μ 与一般新生儿的头围总体均数符号为μ0相同。 则:H0:μ=4o或H0:u=34.50→=33.89 若Ho不被拒绝:样本信息没有提供充足的证据拒绝Ho。 若Ho被拒绝:样本信息不支持H。,支持备择假设H1。 即H1:L≠o或H1:u≠34.50 在假设H条件成立的情况下,样本均数和总体均数的差异能 否用抽样误差解释
案例中: 假设(检验假设�"):矿区新生儿头围的总体均数符号为μ 与一般新生儿的头围总体均数符号为μ0 相同。 则:�":µ=�" 或 �":µ=34.50 → �*=33.89 若�"不被拒绝:样本信息没有提供充足的证据拒绝�"。 若�"被拒绝:样本信息不支持�",支持备择假设�%。 即�%:µ ≠ �" 或 �%:µ ≠ 34.50 在假设�"条件成立的情况下,样本均数和总体均数的差异能 否用抽样误差解释

案例中: 采用U检验: X~N(4o,02)-→X~N(4o,02/n) 经过U变化,U=-~N(0,1)标准正态分布 oo//n 案例中:n=55,02=1.992 Ho:u=34.50条件下, U= 33.89-34.50 =-2.273 1.99/V55 n -2.273
案例中: 采用U检验: X~N(�", �" &)→ �*~�(�", �" ⁄& �) 经过U变化,U = :*;=⁄ ? ~�(0,1)标准正态分布 案例中:n=55, �" & = 1.99& �": � = 34.50条件下, U = CC.DE;CF.G" %.EE⁄ GG = −2.273
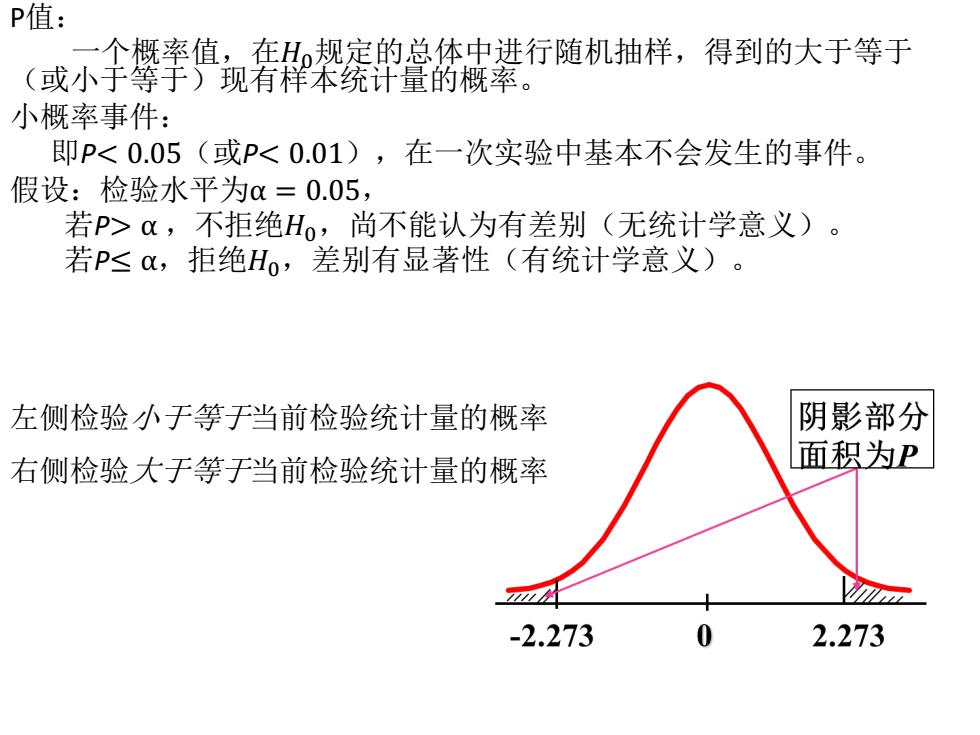
P值: 一个概率值,在H规定的总体中进行随机抽样,得到的大于等于 (或小于等于)现有样本统计量的概率。 小概率事件: 即P,不拒绝Ho,尚不能认为有差别(无统计学意义)。 若P≤,拒绝Ho,差别有显著性(有统计学意义)。 左侧检验小于等于当前检验统计量的概率 阴影部分 右侧检验大于等于当前检验统计量的概率 面积为P A -2.273 0 2.273
P值: 一个概率值,在�"规定的总体中进行随机抽样,得到的大于等于 (或小于等于)现有样本统计量的概率。 小概率事件: 即P α ,不拒绝�",尚不能认为有差别(无统计学意义)。 若P≤ α,拒绝�",差别有显著性(有统计学意义)。 左侧检验小于等于当前检验统计量的概率 右侧检验大于等于当前检验统计量的概率

案例中: 1U|=2.27,U0.05/2=1.96,U0.01/2=2.581 1.96<|U<2.580.01<P<0.05 按所取的检验水准=0.05则拒绝Ho,接受H1, 样本均数与总体均数的差异有统计学意义,可以认 为矿区新生儿的头围与一般新生儿不同,矿区新生 儿的头围小于一般新生儿
案例中: � =2.27,�"."G⁄& = 1.96,�"."%⁄& = 2.581 1.96< � < 2.58 0.01<P<0.05 按所取的检验水准α =0.05则拒绝�",接受�%, 样本均数与总体均数的差异有统计学意义,可以认 为矿区新生儿的头围与一般新生儿不同,矿区新生 儿的头围小于一般新生儿
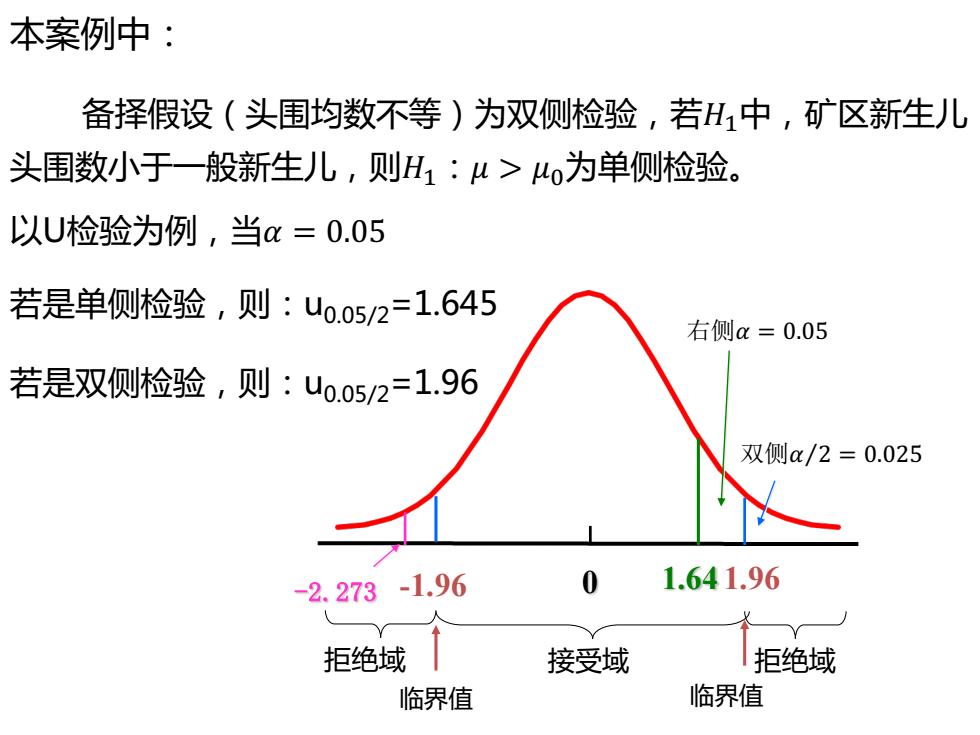
本案例中: 备择假设(头围均数不等)为双侧检验,若H中,矿区新生儿 头围数小于一般新生儿,则H1:u>为单侧检验。 以U检验为例,当a=0.05 若是单侧检验,则:uo.05/2=1.645 右侧a=0.05 若是双侧检验,则:o.05/2=1.96 双侧a/2=0.025 -2.273-1.96 1.641.96 拒绝域 接受域 拒绝域 临界值 临界值
本案例中: 备择假设(头围均数不等)为双侧检验,若�%中,矿区新生儿 头围数小于一般新生儿,则�%:� > �"为单侧检验。 以U检验为例,当� = 0.05 若是单侧检验,则:u0.05/2=1.645 若是双侧检验,则:u0.05/2=1.96 -2.273 -1.96 0 1.64 1.96 右侧� = 0.05 双侧�⁄2 = 0.025 拒绝域 接受域 拒绝域 临界值 临界值