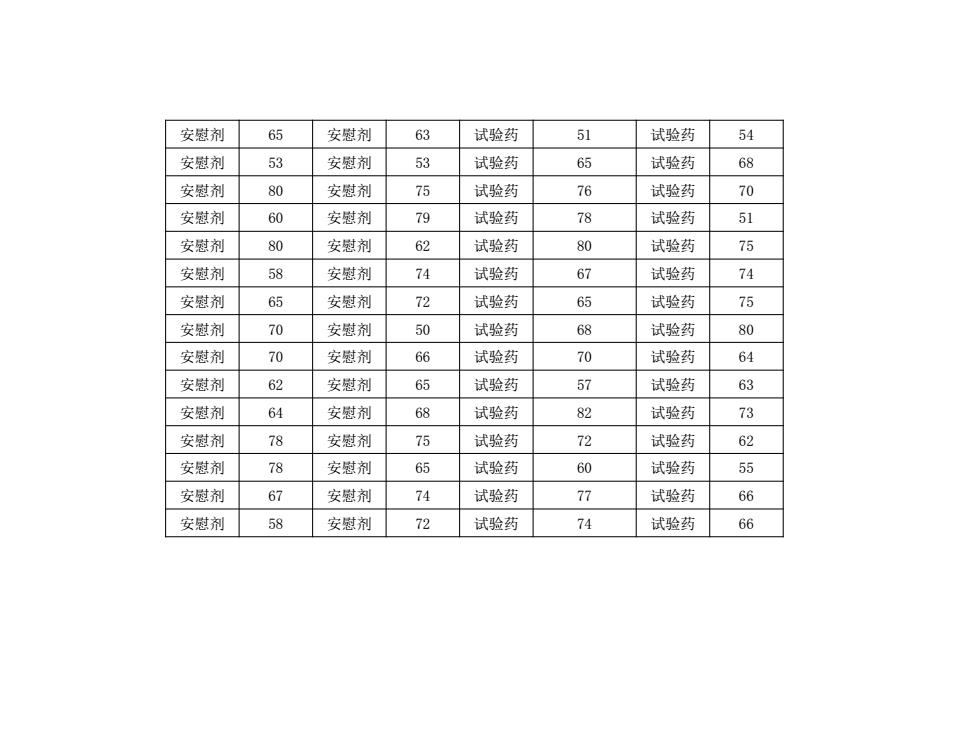
安慰剂 65 安慰剂 63 试验药 51 试验药 54 安慰剂 53 安慰剂 53 试验药 65 试验药 68 安慰剂 80 安慰剂 75 试验药 76 试验药 70 安慰剂 60 安慰剂 79 试验药 78 试验药 51 安慰剂 80 安慰剂 62 试验药 80 试验药 75 安慰剂 58 安慰剂 74 试验药 67 试验药 74 安慰剂 65 安慰剂 72 试验药 65 试验药 75 安慰剂 70 安慰剂 50 试验药 68 试验药 80 安慰剂 70 安慰剂 66 试验药 70 试验药 64 安慰剂 62 安慰剂 65 试验药 57 试验药 63 安慰剂 64 安慰剂 68 试验药 82 试验药 73 安慰剂 78 安慰剂 75 试验药 72 试验药 62 安慰剂 78 安慰剂 65 试验药 60 试验药 55 安慰剂 67 安慰剂 74 试验药 77 试验药 66 安慰剂 58 安慰剂 72 试验药 74 试验药 66
安慰剂 65 安慰剂 63 试验药 51 试验药 54 安慰剂 53 安慰剂 53 试验药 65 试验药 68 安慰剂 80 安慰剂 75 试验药 76 试验药 70 安慰剂 60 安慰剂 79 试验药 78 试验药 51 安慰剂 80 安慰剂 62 试验药 80 试验药 75 安慰剂 58 安慰剂 74 试验药 67 试验药 74 安慰剂 65 安慰剂 72 试验药 65 试验药 75 安慰剂 70 安慰剂 50 试验药 68 试验药 80 安慰剂 70 安慰剂 66 试验药 70 试验药 64 安慰剂 62 安慰剂 65 试验药 57 试验药 63 安慰剂 64 安慰剂 68 试验药 82 试验药 73 安慰剂 78 安慰剂 75 试验药 72 试验药 62 安慰剂 78 安慰剂 65 试验药 60 试验药 55 安慰剂 67 安慰剂 74 试验药 77 试验药 66 安慰剂 58 安慰剂 72 试验药 74 试验药 66
正态性检验 ● 正态分布的两个特征:1.正态对称性 2.正态峰:偏度、峰度 方法:1.图示法Q-Q图,P-P图 2.计算法 f(x)
正态分布的两个特征:1. 正态对称性 2. 正态峰:偏度、峰度 方法: 1. 图示法 Q-Q图,P-P图 2. 计算法 x f (x) 正态性检验
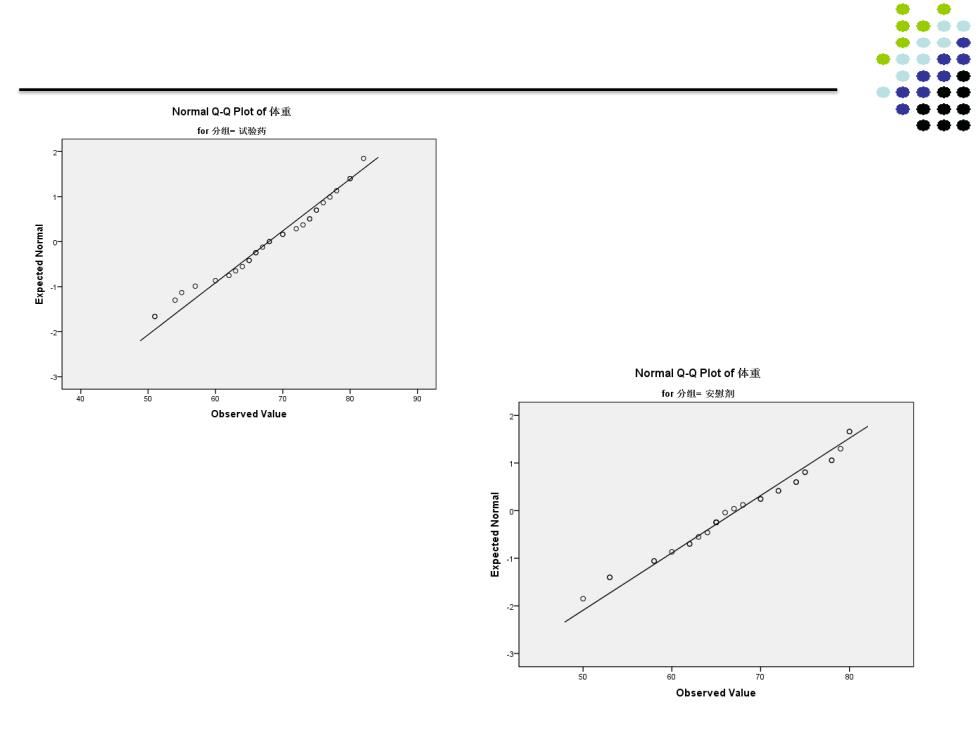
Normal Q-QPlot of体平 for分组-试验药 000 Normal Q-Q Plot of体重 for分组=安慰剂 Observed Value a 60 Observed Value

检验的寇用条件 ◆ 1.随机性 2.正态性一一样本量较小,要求样本是来自正 态分布总体的随机样本 3.方差齐性一一两小样本均数比较,要求两总 体方差相等 4
1. 随机性 2. 正态性--样本量较小,要求样本是来自正 态分布总体的随机样本 3. 方差齐性--两小样本均数比较,要求两总 体方差相等 4 t检验的应用条件

两独立样本方差齐性检验 方差齐性(homoscedasticity) 建立假设 Ho:o1-022 (两总体方差相等) H:O2≠o2 (两总体方差不等) 检验统计量 S2(较大) U1=n1-1,U2=n2-1 S(较小 5
方差齐性(homoscedasticity) 建立假设 H0: s1 2=s2 2 (两总体方差相等) H1: s1 2≠s2 2 (两总体方差不等) 检验统计量 , 1 1 ( ) ( ) 2 1 1 2 2 2 2 1 = = n - = n - S S F u ,u 较小 较大 5 两独立样本方差齐性检验

例题4:方差齐性检验 解:1.建立假设,确定检验水准 H,σ2=o2(两总体方差相等) Hσ≠o,2(两总体方差不等) ou=0.05(双侧检验) 2.计算统计量 F=了=75.16 S 0=29 02=29 68.930 =1.09, 6
解:1. 建立假设,确定检验水准 H0: s1 2=s2 2 (两总体方差相等) H1: s1 2≠s2 2 (两总体方差不等) a=0.05(双侧检验) 2. 计算统计量 1.09 , 30 30 68.930 75.168 2 1 2 2 2 1 = = = u = ,u = S S F 6 例题4:方差齐性检验 29 29

例题4:方差齐性检验 3.确定P值,作出统计决策 P>0.05,按=0.05检验水准不拒绝H,两组 总体方差的差别无统计学意义,故尚不能认为 两组总体方差不等。 7
3. 确定P值,作出统计决策 P>0.05,按a=0.05检验水准不拒绝H0 ,两组 总体方差的差别无统计学意义,故尚不能认为 两组总体方差不等。 7 例题4:方差齐性检验