
前提假设:X,)服从正态分布 →可以较好的估计总体相关系数P 若(X,)不服从二元正态分布呢? Spearman提出对 数据作秩变换后 再计算直线相关 系数 1
前提假设:(X, Y)服从正态分布 à r 可以较好的估计总体相关系数 r 若(X, Y)不服从二元正态分布呢? Spearman提出对 数据作秩变换后 再计算直线相关 系数 1

Spearman秩和相关 r,-Spearman秩相关系数 间接反映X、间的相关性, 且不依赖X、Y的分布。 X、Y→K、W,5,n Σ.②n公wΣ】” n 2
rs-Spearman秩相关系数 间接反映X、Y间的相关性, 且不依赖X、Y的分布。 2 2 ( ) V VW S VV WW V VW l r l l XY VW V VW l V l VW n n ¾¾¾® = = å å - å åå = - 、 秩变换 、 , , Spearman秩和相关 2

● 若个X、Y值均互不相等(不同秩), 51 6∑d n(n2-1) 当n>14时,t= ,=n-2 1-rs n-2 3
2 2 2 6 1 ( 1) 14 2 1 2 S S S d r n n r t n nXY r n n u = - - = = - - - > å 若 个 、 值均互不相等(不同秩), 当 时, , 3

例4 调查了某地区10个乡的钉螺密度与血 吸虫感染率(%)数据如表7。试分析该地区 钉螺密度与感染率之间有无相关关系?
例4 调查了某地区10个乡的钉螺密度与血 吸虫感染率(%)数据如表7。试分析该地区 钉螺密度与感染率之间有无相关关系? 4
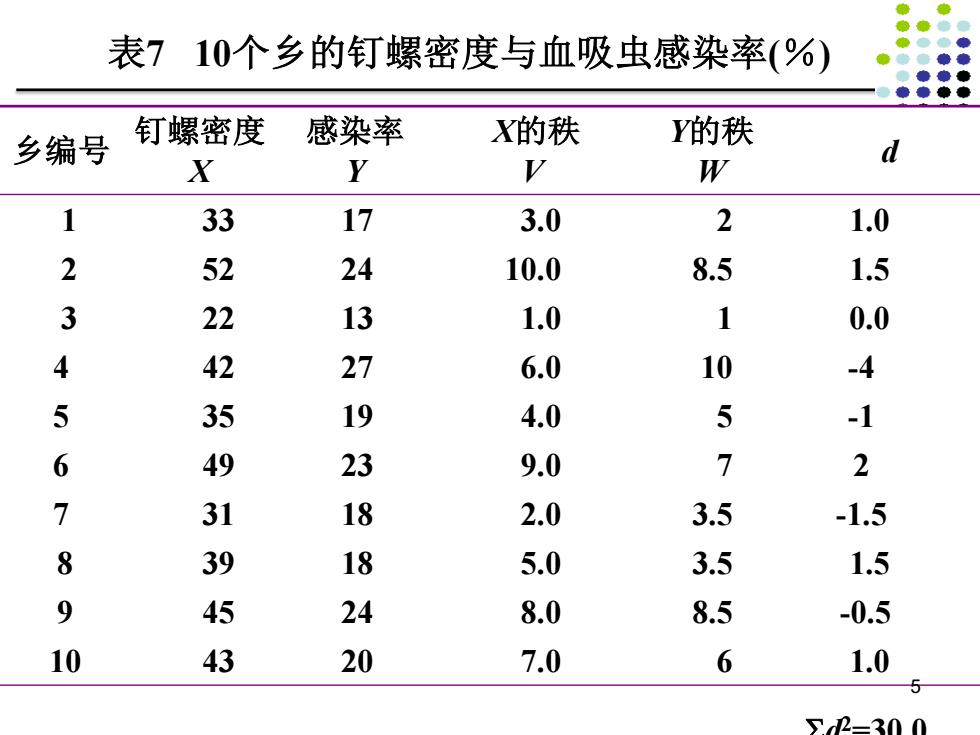
表710个乡的钉螺密度与血吸虫感染率(%) 乡编号 钉螺密度 感染率 X的秩 Y的秩 d X Y V W 1 33 17 3.0 2 1.0 2 52 24 10.0 8.5 1.5 3 22 13 1.0 1 0.0 4 42 27 6.0 10 -4 5 35 19 4.0 5 -1 6 49 23 9.0 7 2 7 31 18 2.0 3.5 -1.5 8 39 18 5.0 3.5 1.5 9 45 24 8.0 8.5 -0.5 10 43 20 7.0 6 1.0 ∑2=300
乡编号 钉螺密度 X 感染率 Y X的秩 V Y的秩 W d 1 33 17 3.0 2 1.0 2 52 24 10.0 8.5 1.5 3 22 13 1.0 1 0.0 4 42 27 6.0 10 -4 5 35 19 4.0 5 -1 6 49 23 9.0 7 2 7 31 18 2.0 3.5 -1.5 8 39 18 5.0 3.5 1.5 9 45 24 8.0 8.5 -0.5 10 43 20 7.0 6 1.0 Sd2=30.0 表7 10个乡的钉螺密度与血吸虫感染率(%) 5

解:感染率-一般不服从正态分布,故计算 Spearmani秩相关。 10个X、Y值均互不相等(不同秩), 故5=1-6∑d =1 6×30 =0.8171 n(n2-1) 10(102-1) 1.建立假设检验,确定检验水准 H:Pps=0(不存在相关关系) H1:ps≠0(有相关关系) 0=0.05 6
解:感染率-一般不服从正态分布,故计算 Spearman秩相关。 1. 建立假设检验,确定检验水准 H0: rS = 0 (不存在相关关系) H1: rS ¹ 0 (有相关关系) a=0.05 2 2 2 6 6 30 1 1 0.8171 ( 1) 10(10 1) S d r n n X Y ´ = - = - = - - å 10个 、 值均互不相等(不同秩), 故 6

2.查表法 查附表14,得s000.745
2. 查表法 查附表14,得rS,0.01=0.745t0.01/2,8,故P<0.01。 在a=0.05水准上拒绝H0,接受H1,即可以认为该 地区钉螺密度与感染率之间有相关关系。 2 2 0.8171 4.01 2 8 1 1 0.8171 2 10 2 S S r t n r n == == u - = - - - - , 7