
糖尿病患者 某人群 饲料 12只大白鼠 中华人民共和国 中华人民其和国 结黛证 龄婚证 生育数量 婚姻状况
糖尿病患者 某人群 饲料 12只大白鼠 婚姻状况 生育数量

案例: 用某饲料喂养12只大白鼠,得出大鼠进食量与体重 增加量如表1。试分析大鼠的进食量和体重增加量 之间的回归关系
案例: 用某饲料喂养12只大白鼠,得出大鼠进食量与体重 增加量如表1。试分析大鼠的进食量和体重增加量 之间的回归关系
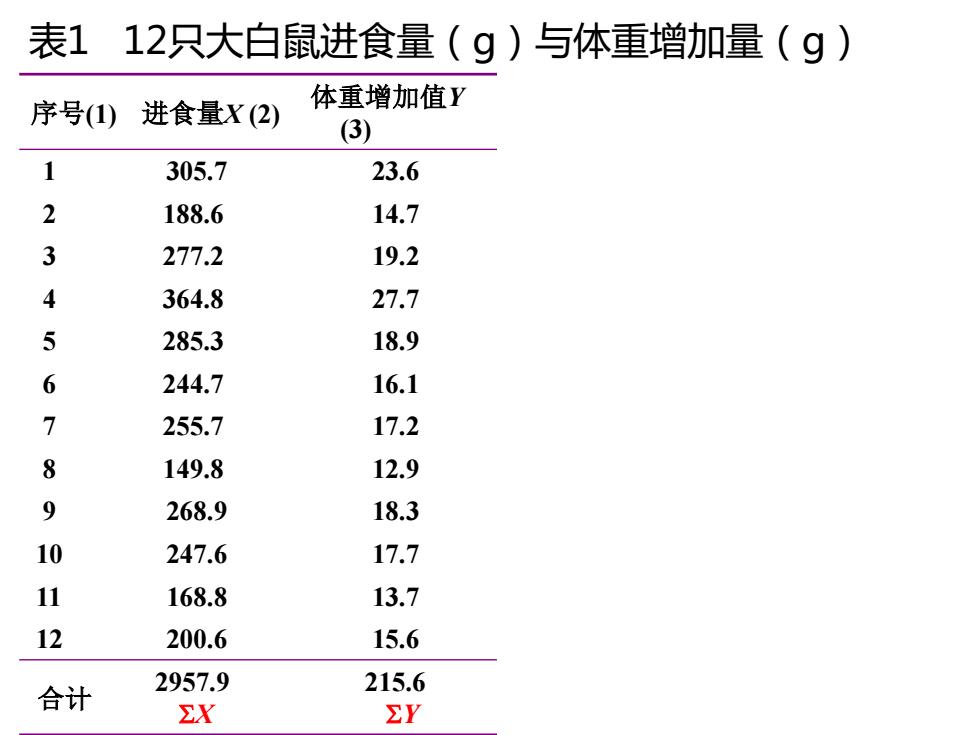
表112只大白鼠进食量(g)与体重增加量(g) 序号()进食量X(2) 体重增加值Y (3) 1 305.7 23.6 2 188.6 14.7 3 277.2 19.2 4 364.8 27.7 5 285.3 18.9 6 244.7 16.1 7 255.7 17.2 8 149.8 12.9 9 268.9 18.3 10 247.6 17.7 11 168.8 13.7 12 200.6 15.6 合计 2957.9 215.6 X EY
序号(1) 进食量X (2) 体重增加值Y (3) X2 (4) Y2 (5) XY (6) 1 305.7 23.6 93452.49 556.96 7214.52 2 188.6 14.7 35569.96 216.09 2772.42 3 277.2 19.2 76839.84 368.64 5322.24 4 364.8 27.7 133079.04 767.29 10104.96 5 285.3 18.9 81396.09 357.21 5392.17 6 244.7 16.1 59878.09 259.21 3939.67 7 255.7 17.2 65484.81 295.84 4401.48 8 149.8 12.9 22440.04 166.41 1932.42 9 268.9 18.3 72307.21 334.89 4920.87 10 247.6 17.7 61305.76 313.29 4382.52 11 168.8 13.7 28493.44 187.69 2312.56 12 200.6 15.6 40240.36 243.36 3129.36 合计 2957.9 SX 215.6 SY 770487.13 SX2 4066.9 SY2 55825.2 SXY 表1 12只大白鼠进食量(g)与体重增加量(g)
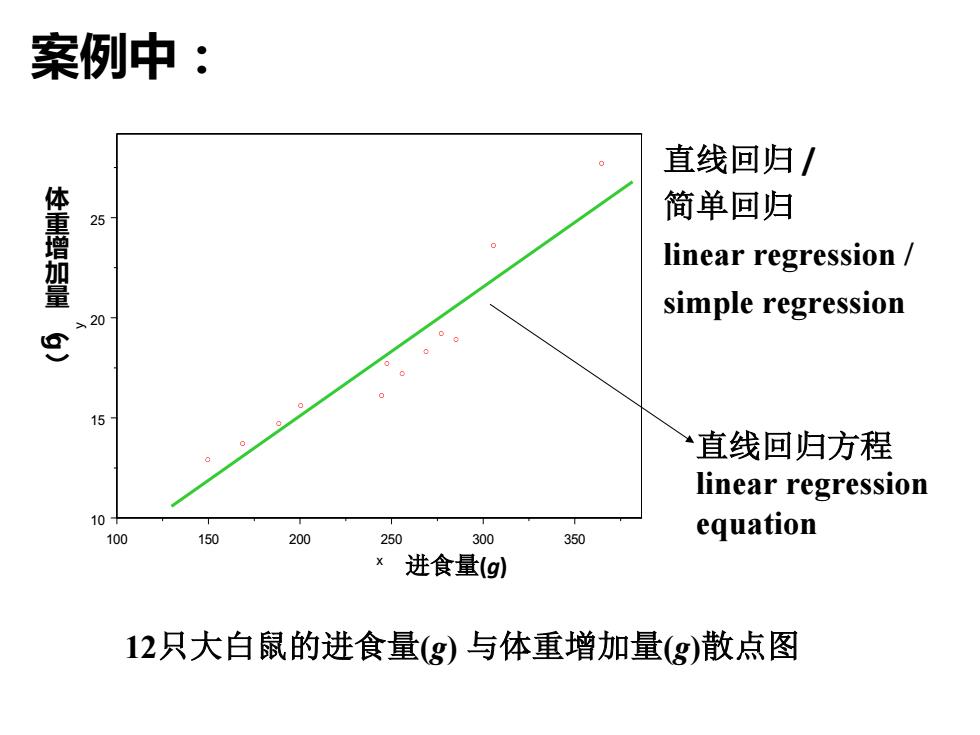
案例中: 直线回归/ 体重增加量 25 简单回归 linear regression simple regression 20 15 “直线回归方程 linear regression 10+ 100 150 200 250 300 350 equation X 进食量(g) 12只大白鼠的进食量(g)与体重增加量(g)散点图
100 150 200 250 300 350 x 10 15 20 25 y 12只大白鼠的进食量(g) 与体重增加量(g)散点图 进食量(g) 体 重 增 加 量 ︵g ︶ 直线回归方程 linear regression equation 直线回归 / 简单回归 linear regression / simple regression 案例中:
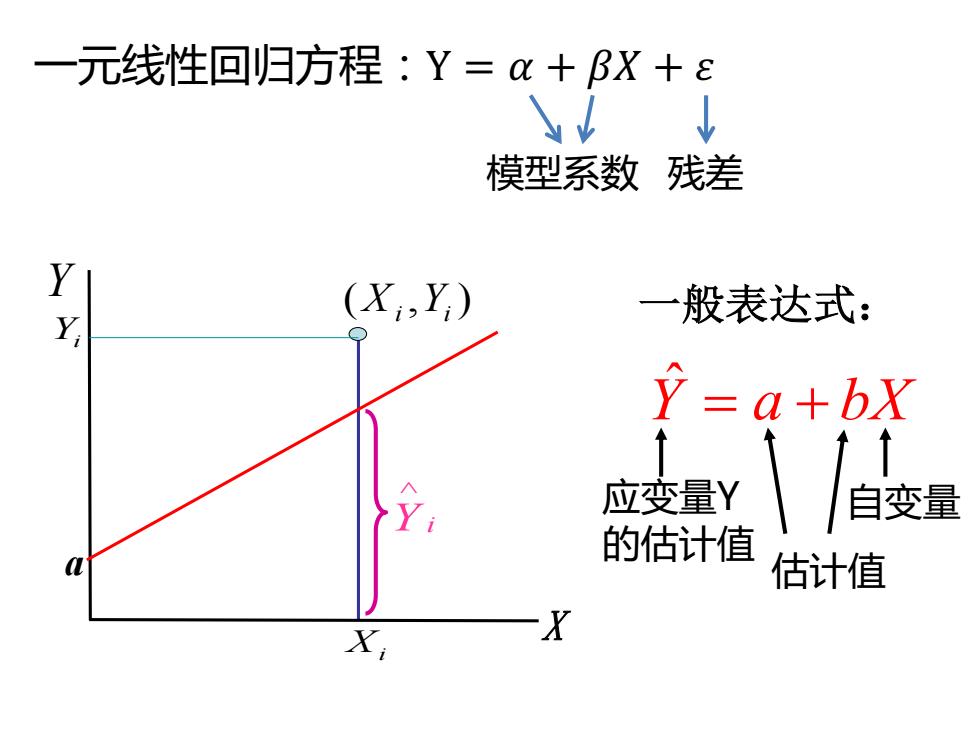
一元线性回归方程:Y=+BX+ 八 ↓ 模型系数残差 (X,Y) 一般表达式: Y=a+bX 应变量Y 的估计值 估计值 Xi X
一般表达式: Y ˆ = a + bX 应变量Y 自变量 的估计值 Xi Y ( , ) Xi Yi Y i Ù X a Yi 一元线性回归方程:Y = � + �� + � 模型系数 残差 估计值

a、b是u、B的估计值。 a:截距(intercept),直线与Y轴交点的纵坐标。 b:斜率(slope),样本回归系数(regression coefficient) 意义:每改变一个单位,平均改变b个单位
a、b是�、�的估计值。 a:截距(intercept),直线与Y轴交点的纵坐标。 b:斜率(slope),样本回归系数(regression coefficient) 意义:X每改变一个单位,Y平均改变b个单位

独立 线性 基本条件 正态 方差齐 了解:均值、标准差、 最大值、最小值、正态分布情况 观察:质量、缺少值、异常值
基本条件 独立 线性 正态 方差齐 了解:均值、标准差、最大值、最小值、正态分布情况 观察:质量、缺少值、异常值

最小二乘法(least square method) 使因变量的观察值(()与估计值()之间的离差平 方和达到最小来求得和b的方法。即: Q(a.b-(-a-x)min
2 22 11 1 ˆ ( , ) () ( ) min nn n i i ii ii i Qab YY Ya bX e == = = åå å - = - - = ® 使因变量的观察值(Y)与估计值(� ()之间的离差平 方和达到最小来求得a和b的方法。即: 最小二乘法(least square method)

该方程组有唯一的一组解,即: 6=∑(x-Y-D_1z ∑(X-X)2 a=Y-bX ∑(y,-)=0 过点(x,)
( ) ( ) ˆ 0 , Y Y i i X Y å - = 过点 2 ( )( ) ( ) XY XX X XY Y b X X a l Y b l X - - = = - = - å å 该方程组有唯一的一组解,即:
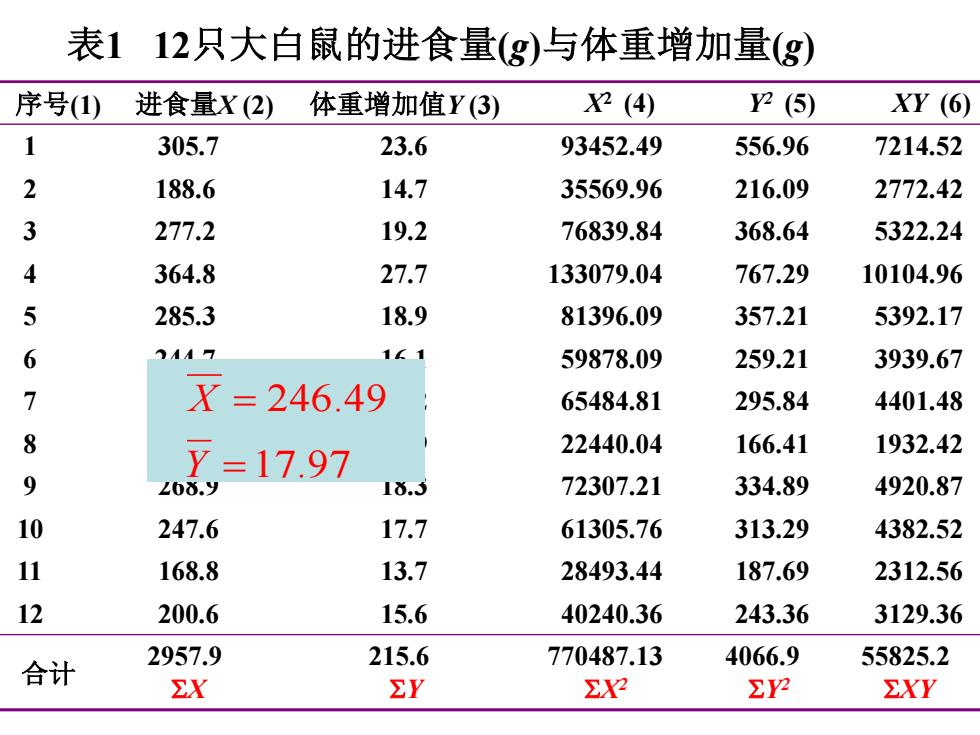
表112只大白鼠的进食量(g)与体重增加量(g) 序号(①)进食量X(2) 体重增加值Y(3) 2(4) 2(⑤) XY(⑥ 1 305.7 23.6 93452.49 556.96 7214.52 2 188.6 14.7 35569.96 216.09 2772.42 3 277.2 19.2 76839.84 368.64 5322.24 4 364.8 27.7 133079.04 767.29 10104.96 5 285.3 18.9 81396.09 357.21 5392.17 6 0447 141 59878.09 259.21 3939.67 7 X=246.49 65484.81 295.84 4401.48 8 7=17.97 22440.04 166.41 1932.42 9 20ǒ. 18.3 72307.21 334.89 4920.87 10 247.6 17.7 61305.76 313.29 4382.52 11 168.8 13.7 28493.44 187.69 2312.56 12 200.6 15.6 40240.36 243.36 3129.36 2957.9 215.6 770487.13 4066.9 55825.2 合计 EX EY X EY EXY
序号(1) 进食量X (2) 体重增加值Y (3) X2 (4) Y2 (5) XY (6) 1 305.7 23.6 93452.49 556.96 7214.52 2 188.6 14.7 35569.96 216.09 2772.42 3 277.2 19.2 76839.84 368.64 5322.24 4 364.8 27.7 133079.04 767.29 10104.96 5 285.3 18.9 81396.09 357.21 5392.17 6 244.7 16.1 59878.09 259.21 3939.67 7 255.7 17.2 65484.81 295.84 4401.48 8 149.8 12.9 22440.04 166.41 1932.42 9 268.9 18.3 72307.21 334.89 4920.87 10 247.6 17.7 61305.76 313.29 4382.52 11 168.8 13.7 28493.44 187.69 2312.56 12 200.6 15.6 40240.36 243.36 3129.36 合计 2957.9 SX 215.6 SY 770487.13 SX2 4066.9 SY2 55825.2 SXY 表1 12只大白鼠的进食量(g)与体重增加量(g) 17.97 246.49 = = Y X