石河子大学：《医学统计学》课程教学课件（2014）第02章 定量数据的统计描述

2015/1/9 回回 课程设置 恋石河于大学 课时：理论课：22学时 实习课：10学时 联系方式：预防医学系卫生统计学教室 第二章定量数据的统计描述 2057153 (Quantitative data statistical Baidu贴吧：yfyx(讨论、答疑、作业) description) 大学精品课程网站 损防医学杂 教学资源(ppt.wmy） ■ 第一节频数分布 ,如表所示： (Frequency Distribution) 4.765265.615.954.464.574.315.18 由奔脸或临床现泰等各种方式得到的原地款 4.924274.774.885.004.73447534 据，和暴是计亚资料异且现察的创款教多， 4.704814935.044405274.63550 为丁能修是示款据的分布规神，可以对款据 5244.974.714.444.945.054.784.52 进行分血，然后制作频散表成脸制直方国。 4.63.5.024.76 ■ 一，k表(Frequency Table) 38设含量金R=之义本R=595 表列出观指每的可取区间及美 (2)填支血题：有年而血之洞的延嘉，取类子资 1.墙克颜放k道常透拆在8一15之间 2.确走血距：参考鱼矩为刷k,R为金延 3,确发氢限：店特会★业习情 3童大领度自上下展：年收的体点稀氨段的 4.对各触酸计放：刻记或由放件壳成 最每必须能如属子禁一敏。去际血展在春饭中只包 香下限而不包香上限。 技数 1

2015/1/9 1 第二章 定量数据的统计描述 （Quantitative data statistical description） 预防医学系 1 2 课程设置  课时： 理论课： 22学时 实习课： 10学时 联系方式：预防医学系卫生统计学教研室 Tel.： 2057153 Baidu贴吧：yfyxx （讨论、答疑、作业） http://tieba.baidu.com/f?kw=yfyxx# 大学精品课程网站→教学资源→（ppt、wmv） http://eol.shzu.edu.cn/eol/jpk/course/layout/default/index.jsp?courseId=1204 2 第一节 频数分布 (Frequency Distribution) 由实验或临床观察等各种方式得到的原始数 据，如果是计量资料并且观察的例数较多， 为了能够显示数据的分布规律，可以对数据 进行分组，然后制作频数表或绘制直方图。 3 例2-1 某地用随机抽样方法检查了140名成年男子的 红细胞数，检测结果如表所示： 如何有效地组织、整理和表达数据的信息？ 4.76 5.26 5.61 5.95 4.46 4.57 4.31 5.18 4.92 4.27 4.77 4.88 5.00 4.73 4.47 5.34 4.70 4.81 4.93 5.04 4.40 5.27 4.63 5.50 5.24 4.97 4.71 4.44 4.94 5.05 4.78 4.52 4.63 …… 5.02 4.76 4 一、频数表 (Frequency Table) 频数表：同时列出观察指标的可能取值区间及其 在各区间内出现的频数。 1.确定组数k：通常选择在8～15之间 2.确定组距： 参考组距为R/k , R为全距 3.确定组限: 应符合专业习惯 4.对各组段计数：划记或由软件完成 5 （1）确定全距 全距R＝xmax－xmin，本例R＝5.95- 3.82＝2.13 （2）确定组距：相邻两组之间的距离，取决于资 料的性质和组段数。常以全距的十分之一估计。组 段数通常取8-15组。将全距除以组数可得到组据的 近似值：组距=全距/组数。，若分10组，则参考组 距为i= R /10=2.13/10≈0.21。 （3）确定组段的上下限：各组段的终点称组段的 上限，起点称组段的下限。整个资料范围的每一个 数据必须能归属于某一组。实际组限在每组中只包 含下限而不包含上限。 （4）列表整理：写出各组段的频数：用划记法将 所有数据归纳到各组段，得到各组段的频数。 6

2015/1/9 表2-2盖地140名正者易子包感教的期数表 三、期教表的用波 1,保为藤速资拼的形或 2,便于观春款施的会布真型 3,指述计量资料分车的暴中施券不高长地影 4.便于发观资科中合有的朵常值（板火板小值） 5.可眉春鱼段的频中作为机平的传计值 5.00-6.00 三、有数分布因 "1寺用Histogram) 直见、形录地表赤频款会有的形毒和精征。 ”计量资料一直方因 ,以暴直条段代表频数分韦的一种因形 纵轴为各血的频数，機轴为各组的组限 从中可以看出数据的分韦背点： 44 频款分布的真型 正春舟布 :高年位于中来，左右两创的频数大体对餐 对棒 其老对 ·R终投e树2支量中位五· 血清季南康普州 平的水平指标 (对数三备命市)】 ▣②高最趋参(tendency of dispers w色 住里施线， 支水平指标 2

2015/1/9 2 红细胞数 划记 频 数 频 率(%) 累积频率(%) 3.80～ 2 1.4 1.41 4.00～ 正 6 4.3 5.71 4.20～ 正正 11 7.9 13.57 4.40～ 正正正正正 25 17.9 31.43 4.60～ 正正正正正正 32 22.9 54.29 4.80～ 正正正正正 27 19.3 73.57 5.00～ 正正正 17 12.1 85.71 5.20～ 正正 13 9.3 95.00 5.40～ 正 4 2.9 97.86 5.60～ 2 1.4 99.29 5.80～6.00 1 0.7 100.00 表2-2 某地140名正常男子红细胞数的频数表 7 三、频数表的用途 1.作为陈述资料的形式 2.便于观察数据的分布类型 3.描述计量资料分布的集中趋势和离散趋势 4.便于发现资料中含有的异常值（极大极小值） 5.可用各组段的频率作为概率的估计值 8 三、频数分布图  计量资料－直方图  以垂直条段代表频数分布的一种图形  纵轴为各组的频数，横轴为各组的组限  从中可以看出数据的分布特点： 9 图2-1 140名正常男子红细胞计数的直方图 直方图（Histogram） 直观、形象地表示频数分布的形态和特征。 10  高峰位于中央，左右两侧的频数大体对称  ①集中趋势(central tendency):变量值集中位置。 数据多集中在“4.6～”附近。 ——平均水平指标  ②离散趋势(tendency of dispersion):变量值围 绕集中位置的分布情况。离“中心”位置越远， 频数越小；且围绕“中心”左右对称。 ——变异水平指标 11 频数分布的类型 正态分布 对称分布 其它对称分布 血清学滴度资料 频数分布 正偏态 （对数正态分布） 其它 偏态分布 负偏态 12

2015/1/9 对称分布与偏态分布 两边低左右对称 1.对静分布 2.偏杰分布 ed tothe right). d 中位重 wed,值中位在教大的一制) 第二节幕中旋尊的统计指标 (一)算术均散葡黎均最(mean) 一，描述集中楚势的特征教 膏用的有： 一道用泰桥：用于反映一服里对兼分有或近服 1.养求始k(arithmetic mean),葡燕均羲(mean 对恭分布款梅的暴中位里成平均水平。 2.元6k(geometric mean) 3.中住k(median) ■ 》计算方法 地140名年男于k(×102几) 4.765265.615.954.464.574.315.18 (1)直楼法会式： 4924274.774.885.004.734.47534 4.704.814.935.044.405274.635.50 52449747刀444.945.054.78452 463…5.024.76 -476+526+561++502+476-47 140

2015/1/9 3 对称分布与偏态分布 1.对称分布 2.偏态分布 右偏态（ skewed to the right），也称正偏态 （positive skewed）,数值集中位置在较小的一侧； 左偏态（ skewed to the left），也称负偏态 （negative skewed）,数值集中位置在较大的一侧； 13 图2-2 59名链球菌咽喉炎患者的潜伏期(h) 0 10 20 30 40 50 60 70 1 3 5 7 9 11 13 15潜伏期(h) 病例数 图2-3 101名正常人的血清肌红蛋白含量 0 5 10 15 20 25 0 5 10 15 20 25 30 35 40 45 50 肌红蛋白含量(ug/mL) 人数 对称分布：中间高、 两边低、左右对称 正偏态分布： 集中在数值小 的一侧 负偏态分布： 集中在数值大 的一侧 0 5 10 15 20 25 30 35 频数 红细胞数（×1012/L） 图4-2 150名正常男子红细胞数的直方图 14 第二节 集中趋势的统计指标 一、描述集中趋势的特征数 统计上使用平均数（average）这一指标体系来 描述一组变量值的集中位置或平均水平。 常用的有： 1. 算术均数(arithmetic mean)，简称均数 (mean) 2. 几何均数(geometric mean) 3. 中位数 (median) 15 （一）算术均数 简称均数（mean） 样本均数用 表示，总体均数用 表示 适用条件：用于反映一组呈对称分布或近似 对称分布数据的集中位置或平均水平。   16 计算方法 （1）直接法 公式 ： n x n x x x x n  i      1 2  17 某地140名成年男子的红细胞数（×1012/L） 4.77 140 4.76 5.26 5.61 5.02 4.76         x 4.76 5.26 5.61 5.95 4.46 4.57 4.31 5.18 4.92 4.27 4.77 4.88 5.00 4.73 4.47 5.34 4.70 4.81 4.93 5.04 4.40 5.27 4.63 5.50 5.24 4.97 4.71 4.44 4.94 5.05 4.78 4.52 4.63 …… 5.02 4.76 18

2015/1/9 >计算方法 (2)加权法（利用频戴表）： 平制：沈计算4,4,4,6,6,8,8,8,10 的始最7 :爱 小++小+“+ 其中X,本组段下限值+下组段下限值 玉=3x4+2x6+3x8+1x10 3+2+3+1 K:频款表的血段款 万频款 组中值 表2小苦地140名正幸器子k如感款的潮款泰 (二)几何均k(geometric mean) 灭。=…x 2 143 1g。=gx+lg+… 正正正 无。=g5】 几何均数：变量 E正 术上 g表示以为底的对数： 数的反对数， =2x39+6x410+ 140 9693-4 140 几何均藏的道用条件与实例 创2-2阅得10人血请浦度的创数分别为 2,2,4,4,8,8,8,8,32,32,求平均请度。 通用条件： X。=92×2×4×4×8×8x8×8×32×32=7 1、乘对称分有，是距较大 2、里倍教头条的等此资料或对教正 春分布（正偏春）资样；知批体 10份么表柳耐抗体放价的平均水平约为1：7 油度、丘清凝幕数价瓷解 时2：3（须成泰要样） 点用：上要用于血黄乎和食生物乎中 4

2015/1/9 4 计算方法 3 2 3 1 3 4 2 6 3 8 1 10           x  举例：试计算4，4，4，6，6，8，8，8，10 的均数？ 19 （2）加权法(利用频数表）： 公式 ： 1 1 2 2 3 3 1 2 3 k k k f X f X f X f X fX X f f f f f               X  本组段下限值+下组段下限值 其中 2 K：频数表的组段数 f：频数 x：组中值 20 红细胞数 划记 频 数 组中值 f X 3.80～ 2 3.9 7.8 4.00～ 正 6 4.1 24.6 4.20～ 正正 11 4.3 47.3 4.40～ 正正正正正 25 4.5 112.5 4.60～ 正正正正正正 32 4.7 150.4 4.80～ 正正正正正 27 4.9 132.3 5.00～ 正正正 17 5.1 86.7 5.20～ 正正 13 5.3 68.9 5.40～ 正 4 5.5 22 5.60～ 2 5.7 11.4 5.80～6.00 1 5.9 5.9 合计 140 - 表2-1 某地140名正常男子红细胞数的频数表 4.7843 140 669.8 140 2 3.9 6 4.10 1 5.9        x  21 （二）几何均数（geometric mean） ) lg lg ( lg (lg lg lg ) 1 lg 1 1 2 1 2 n x X n x x x x n X X x x x i G i G n n G n             ，为正值 表示以 为底的反对数 表示以 为底的对数； 0 lg 10 lg 10 1   X 几何均数：变量 对数值的算术均 数的反对数。 22 几何均数的适用条件与实例 适用条件： 1、非对称分布，差距较大 2、呈倍数关系的等比资料或对数正 态分布（正偏态）资料；如抗体 滴度、血清凝集效价资料 23 例2-2 测得10人血清滴度的倒数分别为 2,2,4,4,8,8,8,8,32,32,求平均滴度。 2 2 4 4 8 8 8 8 32 32 7 10 XG            10份血凝抑制抗体效价的平均水平约为 1:7 7 10 lg 2 lg 2 lg 4 lg 4 lg8 lg8 lg8 lg8 lg32 lg 32 lg 1                   G 例2-3 （频数表资料） 应用：主要用于血清学和微生物学中。 24

2015/1/9 频款表资料的儿何均教 (三)中位数(median) gG滴度倒数例泰F 下gX 中位款是将一轮版插从小亚大林列后位次居 中的文量值，符号为M,反映一北现泰值在 30 位次上的平始水平。 道丽表种：通合各种嘉别的瓷料。北通合 326 696.672 定款值，⑤③资料分布不明等。 G=1g1(698.62326)=139 ■ 中位教计算会式 中接教Median,M 将一观值从小大痛排列，中合位里的 最健即为中位散。 1.原场资科 M=n +)/2 B的量(mg/)为 特燕：仅仅利用了中问的1~2个兼每 M=5.46 (mg/dl) 们为青) 着测量蝽0：0.84、2.85、8.58、9.6，则 M2.85+8.58)/2-5.72(mg/d)m秀s 百分位敲(percentile.) 频散表资料的百分位散 B=L+n-x%-∠） 一血款据从小到火拆列，分成100普分，各 某分香1%的观底值，弃制界展上的盖值业 L:P所在组段下限值 是百分，记为P金部见值的%小 1:组距 于P,而其余(100-划%大于Px。 上：P所在组段的频数 :P,所在组之前各组段的累计频数 36

2015/1/9 5 频数表资料的几何均数                           i n n i i i G f f X f X f X f f X X lg lg lg lg lg lg 1 1 1 1 2 2  IgG滴度倒数 例数,f lgX f·lgX 20 40 80 160 320 640 1280 合计 16 57 76 75 54 25 23 326 1.3010 1.6021 1.9031 2.2041 2.5051 2.8062 3.1072 － 20.96 91.32 144.64 168.08 135.28 70.15 71.47 698.62 G＝lg-1 (698.62/326)＝139 25 （三）中位数（median） 中位数是将一批数据从小至大排列后位次居 中的变量值，符号为M，反映一批观察值在 位次上的平均水平。 适用条件：适合各种类型的资料。尤其适合 于①大样本偏态分布的资料； ②资料有不确 定数值；③资料分布不明等。 26 中位数计算公式 先将观察值按从小到大顺序排列， 再按以下公式计算：          为偶数 为奇数 x x n x n M n n n / 2 1 / 2 2 ( 1)/ 2 特点：仅仅利用了中间的1～2个数据 27 中位数 (Median，M ) 将一组观察值从小到大按顺序排列，居中心位置的 数值即为中位数。 1.原始资料 若测得5个人的VLDL中的apo_B的含量(mg/dl)为 0.84、2.85、5.46、8.58、9.60，则 M=5.46（mg/dl） (n为奇数) 若测量结果：0.84、2.85、8.58、9.6，则 M=(2.85+8.58)/2=5.72（mg/dl） (n为偶数) 28  百分位数 ： 一组数据从小到大 排列，分成100等分，各 等分含1％的观察值，分割界限上的数值就 是百分位数，记为Px。全部观察值的x％小 于Px，而其余（100－x）％大于 Px。 百分位数（percentile） 29 频数表资料的百分位数 所在组之前各组段的累计频数 所在组段的频数 组距 所在组段下限值 ％ L x x x x x x x L x f P f P i L P i f n x f P L : : : : -            30

2015/1/9 ◆ 创 泰24善地6306L单★性A情世插L台量mg0 167 M=070653005-16030=0914 167 M=1+osn- 630 泰24蒂地6306医章女性A请#地上居卡贵mg/圃 分布？ 描述指标？ 30 T分位(Percentile) 百分住款的店用 1.中位款是百分位款的特侧。鼻教燕是不易是开 幸值的彭响，道眉于括述用里德嘉命有、成而满 无款始平均水平。 剑2.5计算侧24始百◆伐长乃5、乃5、乃0. 2括速款桶序列在苏百分位里的水平。多个百分 位最结合使用★凡。不只。可以括述数据的嘉数痕度 5-150,07-4.a01357n R=l60,63000-58.a30=107mw 6

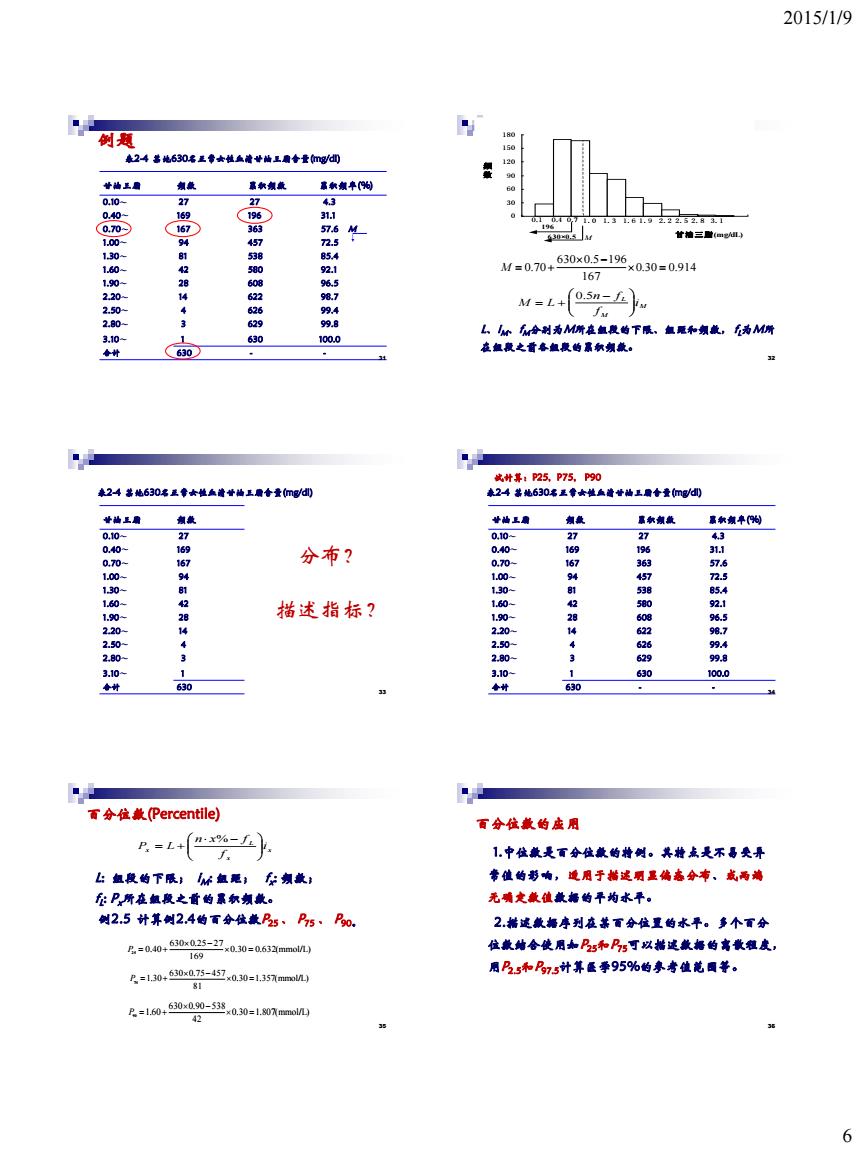
2015/1/9 6 例题 表2-4 某地630名正常女性血清甘油三脂含量(mg/dl) 甘油三脂 频数 累积频数 累积频率(%) 0.10～ 27 27 4.3 0.40～ 169 196 31.1 0.70～ 167 363 57.6 M 1.00～ 94 457 72.5 1.30～ 81 538 85.4 1.60～ 42 580 92.1 1.90～ 28 608 96.5 2.20～ 14 622 98.7 2.50～ 4 626 99.4 2.80～ 3 629 99.8 3.10～ 1 630 100.0 合计 630 - - 31 0 30 60 90 120 150 180 1 频 数 甘油三脂(mg/dL) 0.1 0.4 0.7 1.0 1.3 1.6 1.9 2.2 2.5 2.8 3.1 630×0.5 196 M L、iM、fM分别为M所在组段的下限、组距和频数， f L为M所 在组段之前各组段的累积频数。 0.30 0.914 167 630 0.5 196 0.70     M   M M L i f n f M L            0.5 32 表2-4 某地630名正常女性血清甘油三脂含量(mg/dl) 甘油三脂 频数 0.10～ 27 0.40～ 169 0.70～ 167 1.00～ 94 1.30～ 81 1.60～ 42 1.90～ 28 2.20～ 14 2.50～ 4 2.80～ 3 3.10～ 1 合计 630 33 分布？ 描述指标？ 表2-4 某地630名正常女性血清甘油三脂含量(mg/dl) 甘油三脂 频数 累积频数 累积频率(%) 0.10～ 27 27 4.3 0.40～ 169 196 31.1 0.70～ 167 363 57.6 1.00～ 94 457 72.5 1.30～ 81 538 85.4 1.60～ 42 580 92.1 1.90～ 28 608 96.5 2.20～ 14 622 98.7 2.50～ 4 626 99.4 2.80～ 3 629 99.8 3.10～ 1 630 100.0 合计 630 - - 34 试计算：P25, P75, P90 百分位数(Percentile) L: 组段的下限； iM: 组距； f x : 频数； f L : Px所在组段之前的累积频数。 例2.5 计算例2.4的百分位数P25 、 P75 、 P90。 x x L x i f n x f P L             % 0.30 0.632(mmol/L) 169 630 0.25 27 25 0.40     P   0.30 1.357(mmol/L) 81 630 0.75 457 1.30 75     P   0.30 1.807(mmol/L) 42 630 0.90 538 1.60 90     P   35 百分位数的应用 1.中位数是百分位数的特例。其特点是不易受异 常值的影响，适用于描述明显偏态分布、或两端 无确定数值数据的平均水平。 2.描述数据序列在某百分位置的水平。多个百分 位数结合使用如P25和P75可以描述数据的离散程度， 用P2.5和P97.5计算医学95%的参考值范围等。 36

2015/1/9 第三节变异程度的统计指标 侧3.1对甲乙而名高血压惠★连禁观春5天，副得 的故塘压mmHg结暴★下： 8 148 甲患者 乙患者 两怎者收缩压之间的离散程度此较 闲呢精 (二)四分位间(Quartile (-):差Range) O=P5-B5 七账作金延，即现靠值中录大值和录小值之业，用母 南上一2.4第出，50岁~60步女性浦 号R表示。如首创甲乙雨惠★收喻压的板是分制为 普尚三扇合量的冒分位k乃5不乃5的位重分别为 Rp=186-142=44(mmHg 0.632 mmol/L-1.357mmol/L, 0=1.357-0.632=0.725mmoM) R2=166-159-7(mmHg） 四分住款同距主要用于时壹明是储春分有资料的 越睡葡平丽了、本吾使眉，女眉于花晒传泰病、食 P,=0.40+630x025-22x0.30=0.632mmol 始中套等的最经。量长进使期等。禁点是的昌不数童 -1n,m￥-0w-a2 81 二、平均差指梅 (二)离均善平方和(Sum of Square, 平均偏差=∑r- 为了宽服平狗偏是的能点，可以不道过取能对镇 对于创31： 而是通此取平方来境光王我批随，即使用高焰是 平方不，其计算会或为 乙毒女：平均编整.6-160-12一6-1足.2n s=2x--∑r_灯 季处显，际中少使 5通一个中能计量使眉

2015/1/9 7 第三节 变异程度的统计指标 例3.1 对甲乙两名高血压患者连续观察5天，测得 的收缩压(mmHg)结果如下： 患者 第1天 第2天 第3天 第4天 第5天 均数 甲患者 162 145 178 142 186 162.6 乙患者 164 160 163 159 166 162.4 38 130 140 150 160 170 180 190 0 0.5 1 1.5 2 2.5 两患者收缩压之间的离散程度比较 甲患者 乙患者 39 一、间距指标 （一）极差(Range) 也称作全距，即观察值中最大值和最小值之差，用符 号R 表示。如前例甲乙两患者收缩压的极差分别为 该法简单明了、容易使用，如用于说明传染病、食 物中毒等的最短、最长潜伏期等；缺点是结果不稳定。 R甲 186142  44(mmHg) R乙 166159  7 (mmHg) 39 40 （二）四分位数间距 (Quartile) 如由上一章例2.4 算出，50岁～60岁正常女性血清 甘油三脂含量的百分位数P75和P25的位置分别为 0.632 mmol/L和1.357 mmol/L，则 四分位数间距主要用于衡量明显偏态分布资料的 变异程度。 Q  P75  P25 Q 1.3570.632  0.725(mmol/L) 0.30 0.632(mmol/L) 169 630 0.25 27 2 5 0.40     P   0.30 1.357(mmol/L) 81 630 0.75 457 1.30 7 5     P   40 41 二、平均差距指标 （一）平均偏差(Mean Difference) 如对于例3.1： 甲患者： 乙患者： 特点:直观 , 易理解；但由于用了绝对值，不便于数 学处理，实际中很少使用。 n  X  X 平均偏差  15.52(mmHg) 5 162 162.6 145 162.6 186 162.6          平均偏差 2.32(mmHg) 5 164 162.4 160 162.4 166 162.4          平均偏差 41 42 （二）离均差平方和（Sum of Square，SS） 为了克服平均偏差的缺点，可以不通过取绝对值， 而是通过取平方来避免正负抵消，即使用离均差 平方和，其计算公式为 SS 通常作为一个中间统计量使用。       n X SS X X X 2 2 2 ( ) ( ) 42

2015/1/9 (三)方Variance) "(o)稀准基andard Devaio时 普为是取平女根，还原或与原始观套使平位和两 方业是将高珀是平方和再取平均，即 g-∑x-D2 s∑(x- 的史开重度即为排准姜： 西 位意：对子拆本资样，分零眉的是1，称为 (degree of freedom.df). 树★对子时3.1量计算有 方基的推成：便于款季上的处覆，但南子者平市， ：∑x=813∑x3371Bn=5 麦量衡发生变化，不便于其际虚眉。 S=2.88(mmHg ")支升象最coe价ntfrtion） 小结 C=x100% 故地血软、业腹不表达计量资鲜的信意。 2.平地数是塘速一血观套值燕中位夏或平珀水平船 创3.3侧得某地成年人每聚压均款为77.5mmHg标准 姜为10.7mmHg:女输压6款为122.9mmHg,标准差为 17.1mmHg。比此根舒豪压布收喻压的文乔履麦。 数将分布膏料。 Gas-9票x10o%=15wcas-品lmn=15% 3.百分位款可眉果描述资料的观春健亭列在米百分 位重的水平，中位款是其中的一个精例。 小结 4,描适一血观东值，膝需要表示头平均水平外，还 妻远晒它的高食或文养的情况。 更梅准业和史开果款。 6标准差与灼款雄合色梦完姜地指送一个玉毒会布 对任何多款的正毒分有，每可以道此一个葡华的文 量支换化或梅准正毒分有。利周正春分有可以振求 8

2015/1/9 8 43 （三）方差 (Variance) 方差是将离均差平方和再取平均，即 注意：对于样本资料，分母用的是n-1，称为 自由度(degree of freedom，df )。 方差的特点：便于数学上的处理，但由于有平方， 度量衡发生变化，不便于实际应用。 1 ( ) 2 2     n X X S 43 N X 2 2 (  )    44 （四）标准差 (Standard Deviation) 将方差取平方根，还原成与原始观察值单位相同 的变异量度即为标准差： 例如对于例3.1经计算有 甲患者： 乙患者: 1 ( ) 1 ( ) 2 2 2          n X X n n X X S X 813 133713 2 X  n  5 19.49(mmHg) 5 1 133713 813 / 5 2    S  S  2.88(mmHg) 44 45 （五）变异系数(Coefficient of Variation ) 主要用于对均数相差较大或单位不同的几组观察值的 变异程度进行比较。 例3.3 测得某地成年人舒张压均数为77.5mmHg,标准 差为10.7mmHg；收缩压均数为122.9mmHg,标准差为 17.1mmHg。试比较舒张压和收缩压的变异程度。  100% X S CV 100% 13.8% 77.5 10.7 CV舒张压    100% 13.9% 122.9 17.1 CV收缩压    45 小 结 1. 运用频数表、直方图和统计指标这些技巧能够有 效地组织、整理和表达计量资料的信息。 2.平均数是描述一组观察值集中位置或平均水平的 统计指标，常用的有算术均数、几何均数和中位数。 其中算术均数的应用最为广泛，几何均数则多用于 血清学和微生物学中，中位数主要用于偏度较大的 数据分布资料。 3.百分位数可用来描述资料的观察值序列在某百分 位置的水平，中位数是其中的一个特例。 46 47 小 结 4.描述一组观察值，除需要表示其平均水平外，还 要说明它的离散或变异的情况。 5.衡量变异程度大小的指标有多种: 极差、四分位数 间距、方差、标准差和变异系数。其中应用最多的 是标准差和变异系数。 6.标准差与均数结合能够完整地描述一个正态分布。 对任何参数的正态分布，都可以通过一个简单的变 量变换化成标准正态分布。利用正态分布可以很容 易地确定其数值出现在任意指定范围内的概率。 47