
西名西于大学 ◆目的: 一推断两个总体率或构成此之间有无差别 >推断多个意体年或构成此之问有无差副 第入章X2检脸 ◆检脸统计量:x2 (Chi Square Test 。应用:计数资料 预防医学象芮东升 第一节 日的: 推新西个卷体率(构成此)是否有差到 四格表资料的X2检脸 要求: 两本的两分真个体教列成四格表资料 4 一、基本会式和基本思想 创81为了解中葛海疗原发性高压的 表81两种守法德疗原发性高鱼压的守故 府故,将70名高血压惠者随轨分为两服。比 食计 有丰 验组用诚如辅助海卉,对感组用安慰制如 4a+ 4545 212c 辅助海守,观泰维暴蜘表8-1,问诚苏海对 c+ 原发性高血压是香有数?
第八章 χ2检验 (Chi Square Test Chi Square Test Chi Square Test Chi Square Test ) 预防医学系 芮东升 1 � 目的: � 推断两个总体率或构成比 两个总体率或构成比 两个总体率或构成比 两个总体率或构成比之间有无差别 � 推断多个总体率或构成比 多个总体率或构成比 多个总体率或构成比 多个总体率或构成比之间有无差别 � 检验统计量:χ2 � 应用:计数资料 2 第一节 四格表资料的χ2 检验 3 目的: 推断两个总体率(构成比)是否有差别 推断两个总体率(构成比)是否有差别 推断两个总体率(构成比)是否有差别 推断两个总体率(构成比)是否有差别 要求: 两样本的两分类个体数排列成四格表资料 排列成四格表资料 排列成四格表资料 排列成四格表资料 4 例8.1 为了解某中药治疗原发性高血压的 为了解某中药治疗原发性高血压的 为了解某中药治疗原发性高血压的 为了解某中药治疗原发性高血压的 疗效,将70名高血压患者随机分为两组。试 名高血压患者随机分为两组。试 名高血压患者随机分为两组。试 名高血压患者随机分为两组。试 验组用该药加辅助治疗,对照组用安慰剂加 验组用该药加辅助治疗,对照组用安慰剂加 验组用该药加辅助治疗,对照组用安慰剂加 验组用该药加辅助治疗,对照组用安慰剂加 辅助治疗,观察结果如表 辅助治疗,观察结果如表 辅助治疗,观察结果如表 辅助治疗,观察结果如表8-1,问该药治疗 原发性高血压是否有效? 原发性高血压是否有效? 原发性高血压是否有效? 原发性高血压是否有效? 一、基本公式和基本思想 一、基本公式和基本思想 一、基本公式和基本思想 一、基本公式和基本思想 5 组 别 有效 无效 合计 有效率(%) 对照组 20(25.8) a 24(18.2)b 44(a + b) 45.45 试验组 21(15.2) c 5(10.8)d 26(c + d) 80.77 合 计 41(a + c) 29(b + d) 70(n) 58.57 表8-1 两种疗法治疗原发性高血压的疗效 两种疗法治疗原发性高血压的疗效 两种疗法治疗原发性高血压的疗效 两种疗法治疗原发性高血压的疗效 6

回格表资料的基本形式 。v=(行数-)列数-) 处理组 发生数未发生数 合计 ed 甲 atb 合井此M” ctd元% A:实际频最(actual frequency) 合计 厚◆计% Ti寇论频k(theoretical frequency) TRC:第R行C列的理论频数 n吸:相应的行合计,nc:相店的列金计 ◆ 。检脸统计量X2值反肤了实际频教 与理论频教的项合租度。 女自由度V盒大,X?值也会盒大;所以只 有考虑了自由度V的彭响,x2值才能正 确她反映安际频教A和理论频教了的南合 与屋论频最T制姜不盛诚根大,即晚计量x2不虚诚根 程度。 大。如暴x值根大,即湘对应的P值很小,若P≤ 松脸始自由或取热子可以自由取值的格子象日,局不 的情况下,4个 假设检脸步豫 (2)求检脸统计量值 1)或主检脸复设,喷文检脸水平。 6无二无?中议脸起与对复鱼尚返体有放中和子 t.02,42,2,-os40 行T1卡震)即沈脸鱼与对展血的总体有藏年不等 v=2-IX2-0=1 a=0.05。 2026.24182 21(152510 T-429/m-182 Ta=26(4v70=152
处理组 发生数 未发生数 合计 甲 a b a+b 乙 c d c+d 合 计 a+c b+d n 四格表资料的基本形式 四格表资料的基本形式 四格表资料的基本形式 四格表资料的基本形式 甲% 乙% 合计% T11 T12 T21 T22 % 7 处理组 发生数 未发生数 合计 甲 a b a+b 乙 c d c+d 合 计 a+c b+d n 2 2 ( ) , ( )( 1) A T T χ ν − = Σ = − 行数-1 列数 A:实际频数(actual frequency actual frequency actual frequency actual frequency) T:理论频数(theoretical frequency theoretical frequency theoretical frequency theoretical frequency) TRC :第R 行C 列的理论频数 nR :相应的行合计, :相应的行合计, :相应的行合计, :相应的行合计,nC :相应的列合计 :相应的列合计 :相应的列合计 :相应的列合计 R C RC n n T n = 8 � 检验统计量χ2 值反映了实际频数 与理论频数的吻合程度。 若检验假设H0:π1=π2成立,四个格子的实际频数 成立,四个格子的实际频数 成立,四个格子的实际频数 成立,四个格子的实际频数A 与理论频数T 相差不应该很大,即统计量 相差不应该很大,即统计量 相差不应该很大,即统计量 相差不应该很大,即统计量χ2 不应该很 大。如果χ2 值很大,即相对应的 值很大,即相对应的 值很大,即相对应的 值很大,即相对应的P 值很小,若 P≤ α,则反过来推断 ,则反过来推断 ,则反过来推断 ,则反过来推断A与T相差太大,超出了抽样误差允 相差太大,超出了抽样误差允 相差太大,超出了抽样误差允 相差太大,超出了抽样误差允 许的范围,从而怀疑 许的范围,从而怀疑 许的范围,从而怀疑 许的范围,从而怀疑H0的正确性,继而拒绝 的正确性,继而拒绝 的正确性,继而拒绝 的正确性,继而拒绝H0,接受 其对立假设H1,即π1≠π2 。 9 �自由度ν愈大,χ2 值也会愈大;所以只 值也会愈大;所以只 值也会愈大;所以只 值也会愈大;所以只 有考虑了自由度 有考虑了自由度 有考虑了自由度 有考虑了自由度ν的影响,χ2 值才能正 确地反映实际频数 确地反映实际频数 确地反映实际频数 确地反映实际频数A和理论频数T 的吻合 程度。 检验的自由度取决于可以自由取值的格子数目,而不 检验的自由度取决于可以自由取值的格子数目,而不 检验的自由度取决于可以自由取值的格子数目,而不 检验的自由度取决于可以自由取值的格子数目,而不 是样本含量n。四格表资料只有两行两列 四格表资料只有两行两列 四格表资料只有两行两列 四格表资料只有两行两列,ν=1,即在 周边合计数固定的情况下, 周边合计数固定的情况下, 周边合计数固定的情况下, 周边合计数固定的情况下,4个基本数据当中只有一 个基本数据当中只有一 个基本数据当中只有一 个基本数据当中只有一 个可以自由取值 个可以自由取值 个可以自由取值 个可以自由取值。 10 (1) 建立检验假设,确定检验水平。 建立检验假设,确定检验水平。 建立检验假设,确定检验水平。 建立检验假设,确定检验水平。 H0:π1=π2 即试验组与对照组的总体有效率相等 即试验组与对照组的总体有效率相等 即试验组与对照组的总体有效率相等 即试验组与对照组的总体有效率相等 H1:π1≠π2 即试验组与对照组的总体有效率不等 即试验组与对照组的总体有效率不等 即试验组与对照组的总体有效率不等 即试验组与对照组的总体有效率不等 α=0.05。 假设检验步骤 11 (2)求检验统计量值 )求检验统计量值 )求检验统计量值 )求检验统计量值 2 2 2 2 2 (20 25.8) (24 18.2) (21 15.2) (5 10.8) 8.40 25.8 18.2 15.2 10.8 χ − − − − = + + + = ν = (2 −1)(2 −1) = 1 T11 =44(41/70)=25.8 =44(41/70)=25.8 =44(41/70)=25.8 =44(41/70)=25.8 T12=44(29/70)=18.2 =44(29/70)=18.2 =44(29/70)=18.2 =44(29/70)=18.2 T T T T21=26(41/70)=15.2 =26(41/70)=15.2 =26(41/70)=15.2 =26(41/70)=15.2 T T T T22 = 26(29/70)=10.8 26(29/70)=10.8 26(29/70)=10.8 26(29/70)=10.8 20(25.8) 24(18.2) 21(15.2) 5(10.8) 12
3确定P值,作出推断结论 二、四格表资料检脸的专用会式 (ad-beyn X2= (a+bna+c)bidyc+d) 当自由度v确定后,x分布曲线下右侧尾 都的面积为位时,横轴上相应的x值记作 P<0.005.=0.05水,在H,热H x2=20x5-24×21x70=8.40 44×26×41×29 以认为两原发性高压体有本不学 可认为诚中黄海守原发性高血压有放。 三、四格表资料检脸的校正会式 x2=∑+-71-05 T (ad-bel-n x2= (a+byc+d)a+c)b+d) 时,一板不作校正。 四格表资料x2检脸会式的选梅 倒82某医拳院样调查大四年不 n≥40,T≥5,青用会式 五年版学坐近视眼怎病情况,四年饭学生 的近视来为7.14%,孟年服学生的近视车 n240,1≤T<5,校正金式: 为35.71%,调查结票见表8-2。问该大学 n<40或T<1,直接计算概中。 四平颜与五牛版学生的近视眼怎病平是香 不周?
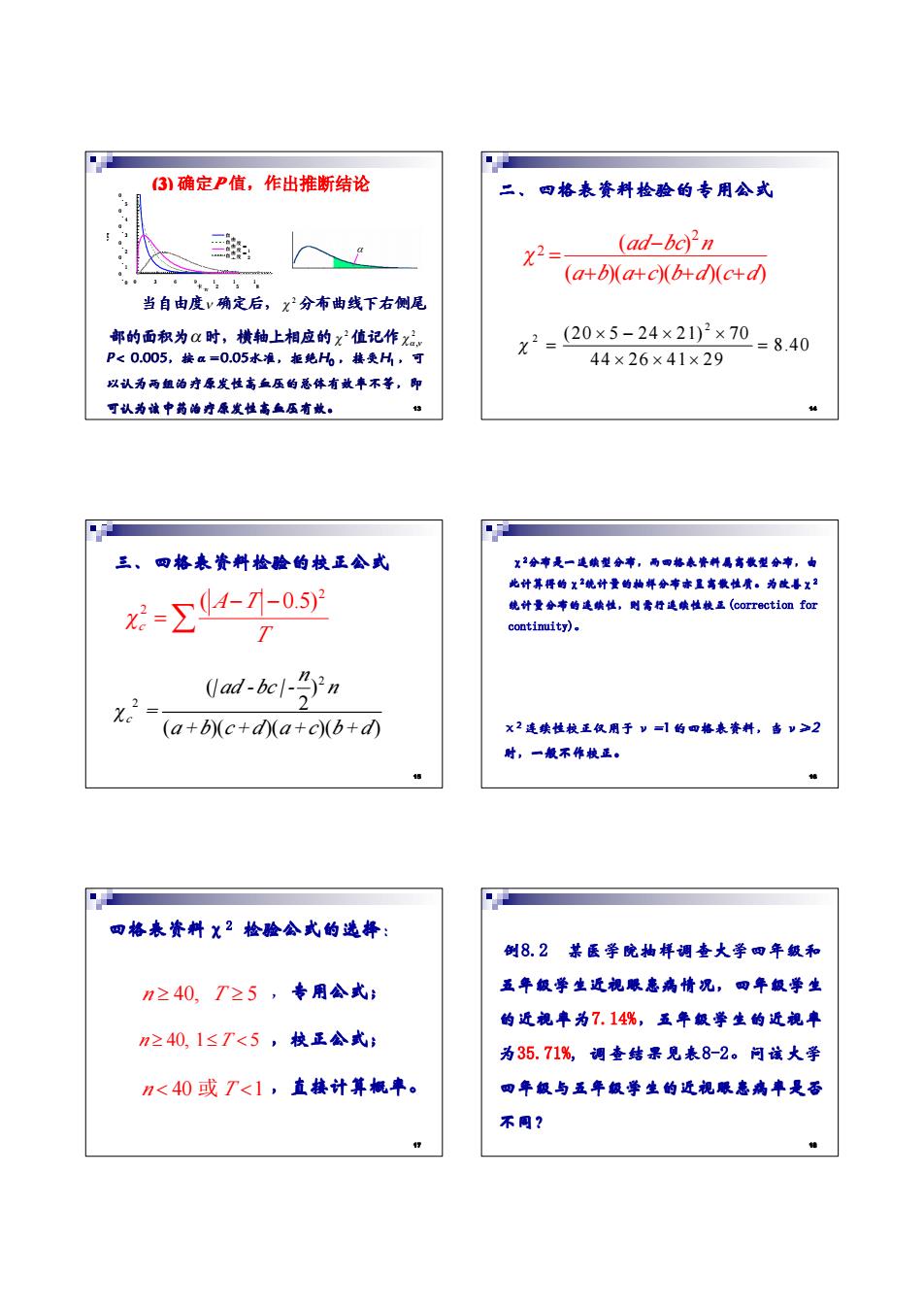
(3) 确定P 值,作出推断结论 当自由度ν 确定后, 2 χ 分布曲线下右侧尾 分布曲线下右侧尾 分布曲线下右侧尾 分布曲线下右侧尾 部的面积为α 时,横轴上相应的 时,横轴上相应的 时,横轴上相应的 时,横轴上相应的 2 χ 值记作 2 χα ,ν 0 . 0 0 . 1 0 . 2 0 . 3 0 . 4 0 . 5 0 3 6 9 1 2 1 5 1 卡 8 方 值 纵 高 自 由 度 = 1 自 由 度 = 2 自 由 度 = 3 自 由 度 = 6 P< 0.005,按α=0.05水准,拒绝H0 ,接受H1 ,可 以认为两组治疗原发性高血压的总体有效率不等,即 以认为两组治疗原发性高血压的总体有效率不等,即 以认为两组治疗原发性高血压的总体有效率不等,即 以认为两组治疗原发性高血压的总体有效率不等,即 可认为该中药治疗原发性高血压有效。 可认为该中药治疗原发性高血压有效。 可认为该中药治疗原发性高血压有效。 可认为该中药治疗原发性高血压有效。 13 二、四格表资料检验的专用公式 二、四格表资料检验的专用公式 二、四格表资料检验的专用公式 二、四格表资料检验的专用公式 2 2 ( ) ( )( )( )( ) ad bc n a b a c b d c d χ − = + + + + 2 2 (20 5 24 21) 70 8.40 44 26 41 29 χ × − × × = = × × × 14 三、四格表资料检验的校正公式 三、四格表资料检验的校正公式 三、四格表资料检验的校正公式 三、四格表资料检验的校正公式 2 2 ( 0.5) c A T T χ − − =∑ 2 2 ( ) 2 ( )( )( )( ) c n | ad - bc | - n = a+b c+d a+c b+d χ 15 χ2分布是一连续型分布,而四格表资料属离散型分布,由 分布是一连续型分布,而四格表资料属离散型分布,由 分布是一连续型分布,而四格表资料属离散型分布,由 分布是一连续型分布,而四格表资料属离散型分布,由 此计算得的χ2统计量的抽样分布亦呈离散性质。为改善 统计量的抽样分布亦呈离散性质。为改善 统计量的抽样分布亦呈离散性质。为改善 统计量的抽样分布亦呈离散性质。为改善χ2 统计量分布的连续性,则需行连续性校正 统计量分布的连续性,则需行连续性校正 统计量分布的连续性,则需行连续性校正 统计量分布的连续性,则需行连续性校正(correction for continuity)。 χ2 连续性校正仅用于 连续性校正仅用于 连续性校正仅用于 连续性校正仅用于ν =1 的四格表资料,当 的四格表资料,当 的四格表资料,当 的四格表资料,当ν≥2 时,一般不作校正。 时,一般不作校正。 时,一般不作校正。 时,一般不作校正。 16 四格表资料χ2 检验公式的选择 检验公式的选择 检验公式的选择 检验公式的选择: n T ≥ ≥ 40, 5 ,专用公式; ,校正公式; ,直接计算概率。 ,直接计算概率。 ,直接计算概率。 ,直接计算概率。 n T ≥ ≤ < 40, 1 5 n T < < 40 1 或 17 例8.2 某医学院抽样调查大学四年级和 某医学院抽样调查大学四年级和 某医学院抽样调查大学四年级和 某医学院抽样调查大学四年级和 五年级学生近视眼患病情况,四年级学生 五年级学生近视眼患病情况,四年级学生 五年级学生近视眼患病情况,四年级学生 五年级学生近视眼患病情况,四年级学生 的近视率为7.14%,五年级学生的近视率 ,五年级学生的近视率 ,五年级学生的近视率 ,五年级学生的近视率 为35.71%, 调查结果见表8-2。问该大学 四年级与五年级学生的近视眼患病率是否 四年级与五年级学生的近视眼患病率是否 四年级与五年级学生的近视眼患病率是否 四年级与五年级学生的近视眼患病率是否 不同? 18

表:丙个年质大季4的近现眼电联未比拉 本養科若不校正时, 02x9-26x51×4 x2=5.49P各组合机平P,的计算 产各组合的概来P服从超几何分有, 在四格表周边合计教不支白条件下, 其和为1。 表内4个实际频数a,b.,Cd支动的组合数 共有“周边合计中豪小教+1”个。蜘创 P-a+6州c+0(a+eb+d0l 83,表内4个实际频教支动的组合教共 alb1lcd小nl 有8+1=9个,见表8-4
表 8-2 两个年级大学生的近视眼患病率比较 年级 近视 非近视 合计 近视率(%) 四年级 2(4.67) 26(23.33) 28 7.14 五年级 5(2.33) 9 (11.67) 14 35.71 合计 7 35 42 16.67 2 2 42 (| 2 9 26 5 | ) 42 2 3.62 (2 5)(26 9)(2 26)(5 9) χc × − × − × = = + + + + P> 0.005,按α=0.05水准,不拒绝H0 ,还 不能认为四年级与五年级学生近视患病率不等。 不能认为四年级与五年级学生近视患病率不等。 不能认为四年级与五年级学生近视患病率不等。 不能认为四年级与五年级学生近视患病率不等。 19 本资料若不校正时, 本资料若不校正时, 本资料若不校正时, 本资料若不校正时, 结论与之相反。 结论与之相反。 结论与之相反。 结论与之相反。 2 χ = 5.49 P < 0.05 20 �条件: �理论依据:超几何分布。 n < 40,或T < 1, 或P ≈ α 时, 四、四格表资料的 四、四格表资料的 四、四格表资料的 四、四格表资料的Fisher确切概率法 21 �基本思想 在四格表周边合计数固定不变的条件 在四格表周边合计数固定不变的条件 在四格表周边合计数固定不变的条件 在四格表周边合计数固定不变的条件 下,计算表内4个实际频数变动时的各种 个实际频数变动时的各种 个实际频数变动时的各种 个实际频数变动时的各种 组合之概率Pi ;再按检验假设用单侧或 ;再按检验假设用单侧或 ;再按检验假设用单侧或 ;再按检验假设用单侧或 双侧的累计概率 双侧的累计概率 双侧的累计概率 双侧的累计概率 P ,依据所取的检验水 ,依据所取的检验水 ,依据所取的检验水 ,依据所取的检验水 准α做出推断。 22 �各组合概率Pi的计算 在四格表周边合计数不变的条件下, 在四格表周边合计数不变的条件下, 在四格表周边合计数不变的条件下, 在四格表周边合计数不变的条件下, 表内4个实际频数 a,b,c,d 变动的组合数 共有“周边合计中最小数 周边合计中最小数 周边合计中最小数 周边合计中最小数+1”个。如例 8.3,表内4个实际频数变动的组合数共 个实际频数变动的组合数共 个实际频数变动的组合数共 个实际频数变动的组合数共 有8+1=9个,见表8-4。 23 �各组合的概率P i服从超几何分布, 服从超几何分布, 服从超几何分布, 服从超几何分布, 其和为1。 ( ) ( )!( )!( )! ! ! ! ! ! i a b c d a c b d P a b c d n + + + + = ! 24

创8.3普17名腾推间意脱出应患者随机分列 两组,分别用西种方黄海疗,结票见表8-3, 问西种疗法的疗放是香不网, 14 294 三、检脸步康(本创n=17<40) 第二节 未创a-1)2.24P-0.041464 ,确定票计瓶本值 配对四格表资料的X2检验 1反饲检普 P=P(1)+P(2)+P()+P(8)+P(9=0.057 (8+P(9)=0.044 创8.4现有198份痰标本,条份标本分别 与计量资料推断西体均是否有差 用A,B两种培养善培养陆核首,陆见 别有成组设计和配对设计一样,计数 表85。问A,B西种墙养基的阳性墙养 资料推断两个意体率(构成比)是否 率是香不等? 有差副也有成组设计和配对设计,即 人 四格表资料和配对四格表资料。 计 13
表 8-3 两种疗法对腰椎间盘脱出症的疗效 疗法 治愈 未治愈 合计 治愈率(%) 新疗法 7 2 9 77.78 保守疗法 2 6 8 25.00 合计 9 8 17 52.94 例8.3 将17名腰椎间盘脱出症患者随机分到 名腰椎间盘脱出症患者随机分到 名腰椎间盘脱出症患者随机分到 名腰椎间盘脱出症患者随机分到 两组,分别用两种方法治疗,结果见表 两组,分别用两种方法治疗,结果见表 两组,分别用两种方法治疗,结果见表 两组,分别用两种方法治疗,结果见表8-3, 问两种疗法的疗效是否不同? 问两种疗法的疗效是否不同? 问两种疗法的疗效是否不同? 问两种疗法的疗效是否不同? 25 表 8-4 各种组合的四格表计算的概率 四格表序号 治愈 未治愈 a-Ta P 1 1 8 8 0 -3.76 0.000370 2 2 7 7 1 -2.76 0.011847 3 3 6 6 2 -1.76 0.096750 4 4 5 5 3 -0.76 0.290251 5 5 4 4 4 0.24 0.362814 6 6 3 3 5 1.24 0.193501 7 * 7 2 2 6 2.24 * 0.041464* 8 8 1 1 7 3.24 0.002962 9 9 0 0 8 4.24 0.000041 *:为实际四格表 26 二、检验步骤( 二、检验步骤( 二、检验步骤( 二、检验步骤(本例n=17<40 n=17<40 n=17<40 n=17<40 ) � 计算表内四个格子数据的各种组合的概率 计算表内四个格子数据的各种组合的概率 计算表内四个格子数据的各种组合的概率 计算表内四个格子数据的各种组合的概率Pi � (表8-4) 本例(a-T)*=2.24, P* =0.041464 � 确定累计概率值 确定累计概率值 确定累计概率值 确定累计概率值 1. 双侧检验 P = P (1) + P (2) + P (7) + P (8) + P (9) =0.057 2. 单侧检验 P = P (7) + P (8) + P (9) =0.044 H 0 : π 1 = π 2 , H 1 : π 1 ≠ π 2 , α = 0 . 0 5 27 第二节 配对四格表资料的 配对四格表资料的 配对四格表资料的 配对四格表资料的 χ2 检验 28 与计量资料推断两总体均数是否有差 与计量资料推断两总体均数是否有差 与计量资料推断两总体均数是否有差 与计量资料推断两总体均数是否有差 别有成组设计和配对设计一样,计数 别有成组设计和配对设计一样,计数 别有成组设计和配对设计一样,计数 别有成组设计和配对设计一样,计数 资料推断两个总体率(构成比)是否 资料推断两个总体率(构成比)是否 资料推断两个总体率(构成比)是否 资料推断两个总体率(构成比)是否 有差别也有成组设计和配对设计,即 有差别也有成组设计和配对设计,即 有差别也有成组设计和配对设计,即 有差别也有成组设计和配对设计,即 四格表资料和配对四格表资料 配对四格表资料 配对四格表资料 配对四格表资料。 29 例8.4 现有198份痰标本,每份标本分别 份痰标本,每份标本分别 份痰标本,每份标本分别 份痰标本,每份标本分别 用A、B两种培养基培养结核菌,结果见 两种培养基培养结核菌,结果见 两种培养基培养结核菌,结果见 两种培养基培养结核菌,结果见 表8-5。问A、B两种培养基的阳性培养 两种培养基的阳性培养 两种培养基的阳性培养 两种培养基的阳性培养 率是否不等? 表8-5 A、B两种培养基的培养结果 B培养基 A培养基 + - 合计 + 48(a ) 24(b ) 72 - 20(c ) 106(d ) 126 合计 68 130 198 30

上递配对设计实脸中,此春个对于而害,两种 合计 处理的暴不外乎者种可能: ①A,B而种检嗣方法曹为阳性教(a, ②A,B两种检司方法曹为阴性教(山: A法为阳性B法为阴性教(): ④A法为阴性、B法为阳性载()。 其中,,d为两法观素结果一致的两种情况 ,为两法观察结果不一致的两种情况。 检脸统计量McNemar test)) 注虑 A培养基的阳性率=a+b)/n,B培养暴的阳性率 b与C两个棒于的理 一威的种况( … b+c>40时: 山。所以,击口很大且&与d的教值很大「即 两法的一或来般高】,b与C的数值物对较小 财,即便是松脸站暴者晚计学意义,具卖际嘉又 9 2 往盆也不大。 v-l *c 检验步骤: :8=C,A:C,a=00 x2=24-202 第三节 =0.36 v= 24+20 行X列表资料的x2检验 P>0.06.按a-0.05水准,不拒绝马 认为两种培养基的阳性培养率相同
表8-5 A、B两种培养基的培养结果 B培养基 A培养基 + - 合计 + 48(a ) 24(b ) 72 - 20(c ) 106(d ) 126 合计 68 130 198 样品号 A培养基 B培养基 1 + + 2 + - 3 - + 4 - - …… …… …… 198 + - 31 上述配对设计实验中,就每个对子而言,两种 上述配对设计实验中,就每个对子而言,两种 上述配对设计实验中,就每个对子而言,两种 上述配对设计实验中,就每个对子而言,两种 处理的结果不外乎有四种可能 处理的结果不外乎有四种可能 处理的结果不外乎有四种可能 处理的结果不外乎有四种可能: ① A、B两种检测方法皆为阳性数 两种检测方法皆为阳性数 两种检测方法皆为阳性数 两种检测方法皆为阳性数(a); ② A、B两种检测方法皆为阴性数 两种检测方法皆为阴性数 两种检测方法皆为阴性数 两种检测方法皆为阴性数 (d); ③ A法为阳性、B法为阴性数 (b); ④ A法为阴性、B法为阳性数 (c)。 其中,a, d 为两法观察结果一致的两种情况, b, c为两法观察结果不一致的两种情况。 32 检验统计量(McNemar test) (McNemar test) (McNemar test) (McNemar test) ( ) ( ) ( ) , 1 1 , 1 2 2 c 2 2 b 2 2 2 2 2 2 2 = + − − = = + − = + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = − = ∑ χ ν χ ν b c b c b c b c b c b c b c b c T A T c A培养基的阳性率 培养基的阳性率 培养基的阳性率 培养基的阳性率=(a+b)/ =(a+b)/ =(a+b)/ =(a+b)/n, B培养基的阳性率 培养基的阳性率 培养基的阳性率 培养基的阳性率 =(a+c)/ =(a+c)/ =(a+c)/ =(a+c)/n, 阳性率的差值= (b-c)/n = (b-c)/n = (b-c)/n = (b-c)/n,若阳性率无差异则 ,若阳性率无差异则 ,若阳性率无差异则 ,若阳性率无差异则B=C b与c两个格子的理论数为 两个格子的理论数为 两个格子的理论数为 两个格子的理论数为(b+c)/2 (b+c)/2 (b+c)/2 (b+c)/2 当b+c≥40时: 当b+c<40时: 33 注意: 本法一般用于样本含量不太大的资料。因为 本法一般用于样本含量不太大的资料。因为 本法一般用于样本含量不太大的资料。因为 本法一般用于样本含量不太大的资料。因为 它仅考虑了两法结果不一致的两种情况 它仅考虑了两法结果不一致的两种情况 它仅考虑了两法结果不一致的两种情况 它仅考虑了两法结果不一致的两种情况(b, c), 而未考虑样本含量 而未考虑样本含量 而未考虑样本含量 而未考虑样本含量n和两法结果一致的两种情况 和两法结果一致的两种情况 和两法结果一致的两种情况 和两法结果一致的两种情况(a, d)。所以,当 n 很大且 a 与 d 的数值很大(即 的数值很大(即 的数值很大(即 的数值很大(即 两法的一致率较高), 两法的一致率较高), 两法的一致率较高), 两法的一致率较高),b 与 c 的数值相对较小 的数值相对较小 的数值相对较小 的数值相对较小 时,即便是检验结果有统计学意义,其实际意义 时,即便是检验结果有统计学意义,其实际意义 时,即便是检验结果有统计学意义,其实际意义 时,即便是检验结果有统计学意义,其实际意义 往往也不大。 34 H 0:B = C,H 1:B ≠ C, α = 0.05 检验步骤: 2 2 (24 20) 0.36 24 20 χ − = = + ν =1 P > 0.05.按α=0.05水准,不拒绝H0 。 认为两种培养基的阳性培养率相同。 35 第三节 行×列表资料的χ2检验 36

行X列表養料 检脸统计量 回多个样本比较时 z2=∑4-1)2 7 有R册2列,聯为R×2泰 ②西个本的此此餐财, x2=- 者2行C列,幕2×C表: @多个样本的构成比此较, v=(行数-1)列数-1) 者RC列,聯RXC表。 >多个样本率的比较 检验乡康: 创8.5#医晚用3种方套性无黄痘型病 :3种方食的有苦 幸肝爽254例,见案雄录见表86,习3种方 油的有数平是香不円。 &=0.05 有(%) -2409+023+010%+0.2边+0.244+0.位9- 0.05格量 样本构成比的比较 检脸步豫 6芝安倒不 b:不同地区人耳血型分车愿体构成比和两 片:不用地区人耳血型分体构威此不或不金相 a=0.05 表黑了三木不用热区由数用木的烟验分有 ¥=(3-14-1)-6 15493251
行×列表资料 ① 多个样本率比较时, 多个样本率比较时, 多个样本率比较时, 多个样本率比较时, 有 R 行 2 列,称为 R ×2表; ② 两个样本的构成比比较时, 两个样本的构成比比较时, 两个样本的构成比比较时, 两个样本的构成比比较时, 有 2 行 C 列,称 2×C 表; ③ 多个样本的构成比比较, 多个样本的构成比比较, 多个样本的构成比比较, 多个样本的构成比比较, 有 R 行 C 列,称为 R ×C 表。 37 检验统计量 2 2 ( 1) ( 1)( 1) R C A n n n χ ν = − = − − ∑ 行数 列数 ∑ − = T A T 2 2 ( ) χ 38 �多个样本率的比较 多个样本率的比较 多个样本率的比较 多个样本率的比较 表 8-6 3 种方案治疗肝炎的疗效 组别 有效 无效 合计 有效率(%) 西药组 51 49 100 51.00 中药组 35 45 80 43.75 中西药结合组 59 15 74 79.73 合计 145 109 254 57.09 例8.5 某医院用3种方案治疗急性无黄疸型病 种方案治疗急性无黄疸型病 种方案治疗急性无黄疸型病 种方案治疗急性无黄疸型病 毒肝炎254例,观察结果见表 例,观察结果见表 例,观察结果见表 例,观察结果见表8-6,问3种疗 法的有效率是否不同。 法的有效率是否不同。 法的有效率是否不同。 法的有效率是否不同。 39 检验步骤: H0:3种治疗方案的有效率相等 种治疗方案的有效率相等 种治疗方案的有效率相等 种治疗方案的有效率相等 H1:3种治疗方案的有效率不等或不全相等 种治疗方案的有效率不等或不全相等 种治疗方案的有效率不等或不全相等 种治疗方案的有效率不等或不全相等 α=0.05 1) 74 109 15 74 145 59 80 109 45 80 145 35 100 109 49 100 145 51 254 ( 2 2 2 2 2 2 2 − × + × + × + × + × + × χ = × = 254 × (0.1794 + 0.2203 + 0.1056 + 0.2322 + 0.3244 + 0.0279 −1) = 22.81 υ= (3-1)(2-1) = 2 P < 0.05 ,在α=0.05的检验水准下, 的检验水准下, 的检验水准下, 的检验水准下, 拒绝H0,接受H1,可以认为三种疗法的有效率不等或不全相等。 ,可以认为三种疗法的有效率不等或不全相等。 ,可以认为三种疗法的有效率不等或不全相等。 ,可以认为三种疗法的有效率不等或不全相等。 40 表 8-7 三个不同地区血型样本的频数分布 地区 A B AB O 合计 亚洲 321 369 95 295 1080 欧洲 258 43 22 194 517 北美洲 408 106 37 444 995 合计 987 518 154 933 2592 �样本构成比的比较 样本构成比的比较 样本构成比的比较 样本构成比的比较 例8.6 某研究人员收集了亚洲、欧洲和北美洲人 某研究人员收集了亚洲、欧洲和北美洲人 某研究人员收集了亚洲、欧洲和北美洲人 某研究人员收集了亚洲、欧洲和北美洲人 的A、B、AB、O血型资料,结果见表 血型资料,结果见表 血型资料,结果见表 血型资料,结果见表8-7,问不 同地区人群ABO血型分类构成比是否不同。 血型分类构成比是否不同。 血型分类构成比是否不同。 血型分类构成比是否不同。 41 检验步骤 H0:不同地区人群血型分布总体构成比相同 :不同地区人群血型分布总体构成比相同 :不同地区人群血型分布总体构成比相同 :不同地区人群血型分布总体构成比相同 H1:不同地区人群血型分布总体构成比不同或不全相同 :不同地区人群血型分布总体构成比不同或不全相同 :不同地区人群血型分布总体构成比不同或不全相同 :不同地区人群血型分布总体构成比不同或不全相同 α=0.05 2 2 2 2 321 369 444 2592( 1) 297.38 987 1080 518 1080 933 995 χ = + + + − = × × × ⋯⋯ ν = − − = (3 1)(4 1) 6 P < 0.05 < 0.05 < 0.05 < 0.05 ,在α=0.05检验水准下,拒绝 检验水准下,拒绝 检验水准下,拒绝 检验水准下,拒绝H0,接受 H1,认为三个不同地区的人群血型分布总体构成比 认为三个不同地区的人群血型分布总体构成比 认为三个不同地区的人群血型分布总体构成比 认为三个不同地区的人群血型分布总体构成比 不同或不全相同。 不同或不全相同。 不同或不全相同。 不同或不全相同。 42

多个样本平间的多重比较 行X列表的分割 >x2分制法(partitions of x2 method) >重新规定检验水准: >Scheffe'可信区问法 I型错误的概率不变。 户SNK法 >检验水准的估计方法: 根据分析目的 1,多个实脸血河的两两此较 a=- 表修时的异值表(供多个形木间的多此用) 2 目- 2 石为样本率的个数 益盘 2。实脸组与同一个对瓶组的比献 为样本率的个数 创87对创8.5中表8-6的资料进行两两此 检脸步豫 秋,以推断是香任西种青法海守急性无黄 ,即任两对比组的总体有效率相等 壶型病幸肝变的有数均省差? ,即任两对比组的总体有效率不等 表63种方肝的爱 创为3个实脸血的两两比
�χ2分割法(partitions of (partitions of (partitions of (partitions of χ2 method) method) method) method) �Scheffe Scheffe Scheffe Scheffe’可信区间法 �SNK法 多个样本率间的多重比较 多个样本率间的多重比较 多个样本率间的多重比较 多个样本率间的多重比较 43 行×列表的分割 �重新规定检验水准: I型错误的概率不变。 �检验水准的估计方法: 根据分析目的 44 1.多个实验组间的两两比较 .多个实验组间的两两比较 .多个实验组间的两两比较 .多个实验组间的两两比较 2 ( 1) 2 − = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ k k k K:为样本率的个数 ' 2 = k α α ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ 2.实验组与同一个对照组的比较 .实验组与同一个对照组的比较 .实验组与同一个对照组的比较 .实验组与同一个对照组的比较 K:为样本率的个数 ' k 1 α α = − 45 表 8-8 ν = 1 时的 2 χ 界值表(供多个样本率间的多重比较用) 2 χ P 2 χ P 2 χ P 6.24 0.01250 7.48 0.00625 8.21 0.00417 6.96 0.00833 7.88 0.00500 8.49 0.00358 7.24 0.00714 8.05 0.00455 8.73 0.00313 46 例8.7 对例8.5中表8-6的资料进行两两比 的资料进行两两比 的资料进行两两比 的资料进行两两比 较,以推断是否任两种疗法治疗急性无黄 较,以推断是否任两种疗法治疗急性无黄 较,以推断是否任两种疗法治疗急性无黄 较,以推断是否任两种疗法治疗急性无黄 疸型病毒肝炎的有效率均有差别? 疸型病毒肝炎的有效率均有差别? 疸型病毒肝炎的有效率均有差别? 疸型病毒肝炎的有效率均有差别? 表8-6 3 种方案治疗肝炎的疗效 组别 有效 无效 合计 有效率(%) 西药组 51 49 100 51.00 中药组 35 45 80 43.75 中西药结合组 59 15 74 79.73 合计 145 109 254 57.09 47 H 0 : π A = π B ,即任两对比组的总体有效率相等 H 1 : π A ≠ π A ,即任两对比组的总体有效率不等 α = 0 .0 5 检验步骤 本例为3个实验组间的两两比较 个实验组间的两两比较 个实验组间的两两比较 个实验组间的两两比较 0.0167 3 0.05 3(3 1)/ 2 ' 0.05 = = − α = 48

创8.8以创8.5中表8-6膏料中的中黄海守焦为对展 对比鱼 组,面药治疗组与中而茜纯合为武脸组,沈分新两 脸鱼与对鱼白卷体有有无是到? ,即各试验组与对照组的总休有效率相等 即各试验组与对凰组的总体有效半不等 本剑为各安脸血与同一对服组的比酸 一对展组此较的P值结票见表89 三,行X列表资料x2检脸的远意事项 可以认为中药与中西药结合治疗肝夷的 有戴率有基开,中西药结合的卉法好于单 1.里论频长:行到表中的春格D1,并L1≤T改用眼向无序RXC表的F1sher确切舰年法 (可用SAS秋件实现)。 3宾际盛用中:对于行列表资件妻振据其分奏类 型和研充日的适用的松脸方法
表 8-9 3 种疗法有效率的两两比较 对比组 有效 无效 合计 2 χ P 西药组 51 49 100 中药组 35 45 80 合计 86 94 180 0.94 >0.0167 中药组 35 45 80 中西药结合组 59 15 74 合计 94 60 154 20.93 <0.00313 <0.00313 <0.00313 <0.00313 西药组 51 49 100 中西药结合组 59 15 74 合计 110 64 174 15.10 <0.00313 <0.00313 <0.00313 <0.00313 49 H 0 : π T = π C ,即各试验组与对照组的总体有效率相等 H 1 : π T ≠ π C ,即各试验组与对照组的总体有效率不等 α = 0 . 0 5 本例为各实验组与同一对照组的比较 本例为各实验组与同一对照组的比较 本例为各实验组与同一对照组的比较 本例为各实验组与同一对照组的比较 各试验组与同一对照组比较的 各试验组与同一对照组比较的 各试验组与同一对照组比较的 各试验组与同一对照组比较的P值结果见表8-9 0.025 3 1 ' = − = α α 例 8.8 以例8.5中表8-6资料中的中药治疗组为对照 资料中的中药治疗组为对照 资料中的中药治疗组为对照 资料中的中药治疗组为对照 组,西药治疗组与中西药结合为试验组,试分析两 组,西药治疗组与中西药结合为试验组,试分析两 组,西药治疗组与中西药结合为试验组,试分析两 组,西药治疗组与中西药结合为试验组,试分析两 试验组与对照组的总体有效率有无差别? 试验组与对照组的总体有效率有无差别? 试验组与对照组的总体有效率有无差别? 试验组与对照组的总体有效率有无差别? 50 可以认为中药与中西药结合治疗肝炎的 可以认为中药与中西药结合治疗肝炎的 可以认为中药与中西药结合治疗肝炎的 可以认为中药与中西药结合治疗肝炎的 有效率有差异,中西药结合的疗法好于单 有效率有差异,中西药结合的疗法好于单 有效率有差异,中西药结合的疗法好于单 有效率有差异,中西药结合的疗法好于单 纯用中药的疗法。尚不能认为西药与中药 纯用中药的疗法。尚不能认为西药与中药 纯用中药的疗法。尚不能认为西药与中药 纯用中药的疗法。尚不能认为西药与中药 治疗肝炎的有效率有差异。 治疗肝炎的有效率有差异。 治疗肝炎的有效率有差异。 治疗肝炎的有效率有差异。 51 1.理论频数:行列表中的各格 .理论频数:行列表中的各格 .理论频数:行列表中的各格 .理论频数:行列表中的各格T≥1,并且1≤T<5的 格子数不宜超过 格子数不宜超过 格子数不宜超过 格子数不宜超过1/5格子总数,否则可能产生偏性。 格子总数,否则可能产生偏性。 格子总数,否则可能产生偏性。 格子总数,否则可能产生偏性。 处理方法有三种: 处理方法有三种: 处理方法有三种: 处理方法有三种: 增大样本含量以达到增大理论频数的目的, 增大样本含量以达到增大理论频数的目的, 增大样本含量以达到增大理论频数的目的, 增大样本含量以达到增大理论频数的目的, 属首选方法,只是有些研究无法增大样本含 属首选方法,只是有些研究无法增大样本含 属首选方法,只是有些研究无法增大样本含 属首选方法,只是有些研究无法增大样本含 量,如同一批号试剂已用完等。 量,如同一批号试剂已用完等。 量,如同一批号试剂已用完等。 量,如同一批号试剂已用完等。 三、行×列表资料 χ2 检验的注意事项 检验的注意事项 检验的注意事项 检验的注意事项 52 �根据专业知识,删去理论频数太小的行或 ,删去理论频数太小的行或 ,删去理论频数太小的行或 ,删去理论频数太小的行或 列,或将理论频数太小的行或列与性质相 列,或将理论频数太小的行或列与性质相 列,或将理论频数太小的行或列与性质相 列,或将理论频数太小的行或列与性质相 近的邻行或邻列合并。例如:不同年龄组 近的邻行或邻列合并。例如:不同年龄组 近的邻行或邻列合并。例如:不同年龄组 近的邻行或邻列合并。例如:不同年龄组 可以合并,但不同血型就不能合并。 可以合并,但不同血型就不能合并。 可以合并,但不同血型就不能合并。 可以合并,但不同血型就不能合并。 �改用双向无序R×C表的Fisher确切概率法 (可用SAS软件实现)。 53 2.多个样本率比较:若所得统计推断为拒绝 .多个样本率比较:若所得统计推断为拒绝 .多个样本率比较:若所得统计推断为拒绝 .多个样本率比较:若所得统计推断为拒绝H0,接 受H1时,只能认为各总体率之间总的来说有差别,但 时,只能认为各总体率之间总的来说有差别,但 时,只能认为各总体率之间总的来说有差别,但 时,只能认为各总体率之间总的来说有差别,但 不能说明任两个总体率之间均有差别。要进一步推断 不能说明任两个总体率之间均有差别。要进一步推断 不能说明任两个总体率之间均有差别。要进一步推断 不能说明任两个总体率之间均有差别。要进一步推断 哪两两总体率之间有差别,需进一步做多个样本率的 哪两两总体率之间有差别,需进一步做多个样本率的 哪两两总体率之间有差别,需进一步做多个样本率的 哪两两总体率之间有差别,需进一步做多个样本率的 多重比较。 3.实际应用中:对于行列表资料要根据其分类类 实际应用中:对于行列表资料要根据其分类类 实际应用中:对于行列表资料要根据其分类类 实际应用中:对于行列表资料要根据其分类类 型和研究目的选用恰当的检验方法。 型和研究目的选用恰当的检验方法。 型和研究目的选用恰当的检验方法。 型和研究目的选用恰当的检验方法。 54

问题? ■卡方检脸的目的是什么? ■卡方检险的适用条件是什么?
问题? � 卡方检验的目的是什么? � 卡方检验的适用条件是什么? 55