石河子大学：《医学统计学》课程教学课件（非预防专业）第10章线性相关与回归.pdf_大学文库

第十章线性相关与回归 (Linear Correlation & Regression ) (Linear Correlation & Regression ) (Linear Correlation & Regression ) (Linear Correlation & Regression ) 预防医学系芮东升 1 线性相关与回归线性相关与回归线性相关与回归线性相关与回归第一节线性相关第二节线性回归第三节线性相关与回归的区别和联系线性相关与回归的区别和联系线性相关与回归的区别和联系线性相关与回归的区别和联系第三节等级相关 2 一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念二、线性相关系数二、线性相关系数二、线性相关系数二、线性相关系数三、相关系数的显著性检验三、相关系数的显著性检验三、相关系数的显著性检验三、相关系数的显著性检验四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项线性相关（linear correlation) 3 � 线性相关(linear correlation)又称简单相关(simple correlation)，用于双变量正态分布(bivariate normal distribution)资料。其性质可由散点图直观的说明。目的：研究两个变量X,Y数量上的相关关系。数量上的相关关系。数量上的相关关系。数量上的相关关系。 � 特点：统计关系一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念 4 150 160 170 180 190 52 50 48 46 44 42 40 一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念一、线性相关的基本概念为直观地判断两个变量之间的关系，可在直角坐标系中把每为直观地判断两个变量之间的关系，可在直角坐标系中把每为直观地判断两个变量之间的关系，可在直角坐标系中把每为直观地判断两个变量之间的关系，可在直角坐标系中把每对（Xi,Yi）值所代表的点绘出来，形成散点图。例如）值所代表的点绘出来，形成散点图。例如）值所代表的点绘出来，形成散点图。例如）值所代表的点绘出来，形成散点图。例如12名男青年身高与前臂长资料绘制的散点图如图所示：年身高与前臂长资料绘制的散点图如图所示：年身高与前臂长资料绘制的散点图如图所示：年身高与前臂长资料绘制的散点图如图所示： 5 6

若一个变量X由小到大（或由大到小），另由小到大（或由大到小），另由小到大（或由大到小），另由小到大（或由大到小），另一变量Y亦相应地由小到大或由大到小，则两个亦相应地由小到大或由大到小，则两个亦相应地由小到大或由大到小，则两个亦相应地由小到大或由大到小，则两个变量的散点图呈直线趋势，我们称这种现象为变量的散点图呈直线趋势，我们称这种现象为变量的散点图呈直线趋势，我们称这种现象为变量的散点图呈直线趋势，我们称这种现象为共变，也就是这两个变量之间有，也就是这两个变量之间有，也就是这两个变量之间有，也就是这两个变量之间有“相关关系”。男青年身高与前臂长散点呈直线趋势，即男青男青年身高与前臂长散点呈直线趋势，即男青男青年身高与前臂长散点呈直线趋势，即男青男青年身高与前臂长散点呈直线趋势，即男青年身材高，前臂亦长，说明身高与前臂长之间存年身材高，前臂亦长，说明身高与前臂长之间存年身材高，前臂亦长，说明身高与前臂长之间存年身材高，前臂亦长，说明身高与前臂长之间存在线性相关关系我们把这种关系称为在线性相关关系我们把这种关系称为在线性相关关系我们把这种关系称为在线性相关关系我们把这种关系称为直线相关。 7 � 1、正相关：y随x的增大而增大，有直线上升的趋势，x与y的变化是同向的； � 2、负相关：y随x的增大而减少，有直线下降的趋势，x与y的变化是反向的； � 3、零相关：无论x增大或减少，y的大小均不受影响； � 4、非线性相关：点的排列呈现某种曲线趋势；两变量间线性相关的性质和密切程度，可以用相关系数 r 表示 8 线性相关用于双变量正态资料双变量正态资料双变量正态资料双变量正态资料。它的性质可由散点图直观地说明。散点图中点的分布即线性相关的观地说明。散点图中点的分布即线性相关的观地说明。散点图中点的分布即线性相关的观地说明。散点图中点的分布即线性相关的方向和相关之间的密切程度，可分为以下几种情况：，可分为以下几种情况：，可分为以下几种情况：，可分为以下几种情况： 1. 1. 1. 1.正相关 2.负相关 3.无相关 9 y x r =-1 y x r =-0.8 y x r =-0.6 y x r =-0.4 10 相关系数的意义与计算 1、意义：相关系数、意义：相关系数、意义：相关系数、意义：相关系数（correlation coefficient correlation coefficient correlation coefficient correlation coefficient）又称 Pearson Pearson Pearson Pearson积差相关系数，用来说明两个随机变量间线性相关积差相关系数，用来说明两个随机变量间线性相关积差相关系数，用来说明两个随机变量间线性相关积差相关系数，用来说明两个随机变量间线性相关关系的密切程度与相关方向。关系的密切程度与相关方向。关系的密切程度与相关方向。关系的密切程度与相关方向。以符号r表示样本相关系数，符号表示其总体相关系数。 2. 计算：样本相关系数的计算公式为 xx yy xy L L L X X Y Y X X Y Y r = − − − − = ∑ ∑ ∑ 2 2 ( ) ( ) ( )( ) 11 相关系数的特点 1.相关系数r是一个无量纲的数值,且 -1≤r≤1; 2.r>0为正相关,r<0为负相关; 3./r/越接近于1,说明相关性越好./r/越接近于 0,说明相关性越差. 12

例10.1 从男青年总体中随机抽取11名男青年组成样本，分别测量每个男青年的身高和前臂长，，分别测量每个男青年的身高和前臂长，，分别测量每个男青年的身高和前臂长，，分别测量每个男青年的身高和前臂长，身高和前臂长均以身高和前臂长均以身高和前臂长均以身高和前臂长均以cm为单位，测量结果如下表为单位，测量结果如下表为单位，测量结果如下表为单位，测量结果如下表所示，试计算身高与前臂长之间的相关系数。所示，试计算身高与前臂长之间的相关系数。所示，试计算身高与前臂长之间的相关系数。所示，试计算身高与前臂长之间的相关系数。编号身高（cm）前臂长（cm） XY X2 Y2 (X) (Y) 1 170 47 7990 28900 2209 2 173 42 7266 29929 1764 3 160 44 7040 25600 1936 4 155 41 6355 24025 1681 5 173 47 8131 29929 2209 6 188 50 9400 35344 2500 7 178 47 8366 31684 2209 8 183 46 8418 33489 2116 9 180 49 8820 32400 2401 10 165 43 7095 27225 1849 11 166 44 3174 28561 2116 合计 1891 500 86185 326081 22810 13 解：， =1891， =89599， =500， =22810， =86185。代入公式(10-2)，得： 1000 .909 11 1891 326081 ( ) 2 2 2 = ∑ − = − = ∑ nX L XX X 82 .727 11 500 22810 ( ) 2 2 2 = ∑ − = − = ∑ nY LYY Y 按公式（10-1）计算相关系数是否相关？方向和密切程度？ 14 r = ？ r = ？通过样本计算的 r 值存在抽样误差，只有假设检验才能推断只有假设检验才能推断只有假设检验才能推断只有假设检验才能推断 15 总体相关程度及方向。相关程度及方向。相关程度及方向。相关程度及方向。三、相关系数的显著性检验三、相关系数的显著性检验三、相关系数的显著性检验三、相关系数的显著性检验与前面讲的其它统计量一样，根据样本资料计算出与前面讲的其它统计量一样，根据样本资料计算出与前面讲的其它统计量一样，根据样本资料计算出与前面讲的其它统计量一样，根据样本资料计算出来的相关系数同样存在来的相关系数同样存在来的相关系数同样存在来的相关系数同样存在抽样误差。即假设在一个。即假设在一个。即假设在一个。即假设在一个X与Y 无关总体中作随机抽样，由于抽样误差的影响，所得无关总体中作随机抽样，由于抽样误差的影响，所得无关总体中作随机抽样，由于抽样误差的影响，所得无关总体中作随机抽样，由于抽样误差的影响，所得的样本相关系数也常常不等于零。的样本相关系数也常常不等于零。的样本相关系数也常常不等于零。的样本相关系数也常常不等于零。因此要判断两个变量因此要判断两个变量因此要判断两个变量因此要判断两个变量X与Y是否真的存在相关关系，是否真的存在相关关系，是否真的存在相关关系，是否真的存在相关关系，仍需根据作总体相关系数ρ是否为零的假设检验。 16 常用的检验方法有两种常用的检验方法有两种常用的检验方法有两种常用的检验方法有两种: 1.按自由度直接查附表按自由度直接查附表按自由度直接查附表按自由度直接查附表11的界值表，得到的界值表，得到的界值表，得到的界值表，得到P 值。 n 2 1 r r 0 t 2 r − − − = ν = n − 2 2.用假设检验法，计算统计量，其公式为： 17 第一种方法 1. 建立检验假设：，即身高与前臂长之间不存在相关关系：；即身高与前臂长之间存在相关关系 2. 计算统计量 =11， =0.8012，自由度 =11-2=9， 3．查 r 界值表，得统计结论查 r 界值表（附表 11），得，因为 r > ，故 P＜0.005，按水准拒绝 H 0 接受 H 1 ，可以认为男青年身高与前臂长之间存在正相关关系。 18

第二种方法 1. 建立同样的检验假设 2. 计算统计量 4 .017 11 2 1 0 .8012 0 .8012 0 2 = − − − t r = ν=11-2=9 3. 查界值表，得统计结论查界值表，得，，P ＜ 0.005，结果与查界值表一致。 19 四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项 ⒈ 线性相关表示两个变量之间的相互关系是双向线性相关表示两个变量之间的相互关系是双向线性相关表示两个变量之间的相互关系是双向线性相关表示两个变量之间的相互关系是双向的，分析两个变量之间到底有无相关关系可首的，分析两个变量之间到底有无相关关系可首的，分析两个变量之间到底有无相关关系可首的，分析两个变量之间到底有无相关关系可首先绘制散点图，散点图呈现出直线趋势时，再，散点图呈现出直线趋势时，再，散点图呈现出直线趋势时，再，散点图呈现出直线趋势时，再作分析。 ⒉ 相关系数的计算只适用于相关系数的计算只适用于相关系数的计算只适用于相关系数的计算只适用于双变量正态分布双变量正态分布双变量正态分布双变量正态分布的情形，如果资料不服从正态分布，应先通过变量情形，如果资料不服从正态分布，应先通过变量情形，如果资料不服从正态分布，应先通过变量情形，如果资料不服从正态分布，应先通过变量变换，使之正态化，再根据变换值计算相关系变换，使之正态化，再根据变换值计算相关系变换，使之正态化，再根据变换值计算相关系变换，使之正态化，再根据变换值计算相关系数，如果不符合条件应进行数，如果不符合条件应进行数，如果不符合条件应进行数，如果不符合条件应进行秩相关计算。 20 慎用相关的情形 21 (a)异常值 (b)分层资料 (c) 、(d)分层资料慎用相关的情形 22 四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项 ⒊ 依据公式计算出的相关系数仅是样本相关系依据公式计算出的相关系数仅是样本相关系依据公式计算出的相关系数仅是样本相关系依据公式计算出的相关系数仅是样本相关系数，它是总体相关系数的一个估计值，与总体数，它是总体相关系数的一个估计值，与总体数，它是总体相关系数的一个估计值，与总体数，它是总体相关系数的一个估计值，与总体相关系数之间存在着相关系数之间存在着相关系数之间存在着相关系数之间存在着抽样误差，要判断两个事，要判断两个事，要判断两个事，要判断两个事物之间有无相关及相关的密切程度，必须作物之间有无相关及相关的密切程度，必须作物之间有无相关及相关的密切程度，必须作物之间有无相关及相关的密切程度，必须作假设检验。 23 四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项四、进行线性相关分析的注意事项 ⒋ 相关分析是用相关系数来描述两个变量间相互相关分析是用相关系数来描述两个变量间相互相关分析是用相关系数来描述两个变量间相互相关分析是用相关系数来描述两个变量间相互关系的密切程度和方向，而两个事物之间的关关系的密切程度和方向，而两个事物之间的关关系的密切程度和方向，而两个事物之间的关关系的密切程度和方向，而两个事物之间的关系既可能是依存因果关系，也可能仅是相互伴系既可能是依存因果关系，也可能仅是相互伴系既可能是依存因果关系，也可能仅是相互伴系既可能是依存因果关系，也可能仅是相互伴随的数量关系。随的数量关系。随的数量关系。随的数量关系。决不可因为两事物间的相关系决不可因为两事物间的相关系决不可因为两事物间的相关系决不可因为两事物间的相关系数有统计学意义，就认为两者之间存在着因果数有统计学意义，就认为两者之间存在着因果数有统计学意义，就认为两者之间存在着因果数有统计学意义，就认为两者之间存在着因果关系，要证明两事物间确实存在因果关系，必要证明两事物间确实存在因果关系，必要证明两事物间确实存在因果关系，必要证明两事物间确实存在因果关系，必须凭借专业知识加以阐明。须凭借专业知识加以阐明。须凭借专业知识加以阐明。须凭借专业知识加以阐明。 24

思考题： 1. 已知：r=0.8 , r=0.8 , r=0.8 , r=0.8 ,结论：两变量密切相关。结论：两变量密切相关。结论：两变量密切相关。结论：两变量密切相关。 2.已知：r=0.8，P<α,结论：两变量密切相关。结论：两变量密切相关。结论：两变量密切相关。结论：两变量密切相关。 3.已知：r=0.08，P<α,结论：? 25 一、线性回归的基本概念一、线性回归的基本概念一、线性回归的基本概念一、线性回归的基本概念二、线性回归方程的计算二、线性回归方程的计算二、线性回归方程的计算二、线性回归方程的计算三、线性回归方程的显著性检验三、线性回归方程的显著性检验三、线性回归方程的显著性检验三、线性回归方程的显著性检验四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项第二节线性回归（linear regression) linear regression) linear regression) linear regression) 26 英国人类学家 F.Galton首次在《自然遗传》一书中，提出并阐明了“相关”和“相关系数”两个概念，为相关论奠定了基础。其后，他和英国统计学家 Karl Pearson对上千个家庭的身高、臂长等指标做了测量，发现：历史背景： 27 � 儿子身高（Y，英寸）与父亲身高（X，英寸）存在线性关系： � 也即高个子父代的子代在成年之后的身高平均来说不是更高，而是稍矮于其父代水平，而矮个子父代的子代的平均身高不是更矮，而是稍高于其父代水平。Galton将这种趋向于种族稳定的现象称之“回归”。 ˆY X = + 33.73 0.516 28 29 “回归”已成为表示变量之间某种数量依存关系的统计学术语，并且衍生出“回归方程” “回归系数”等统计学概念。如研究糖尿病人血糖与其胰岛素水平的关系，研究儿童年龄与体重的关系等。 30

一、线性回归的基本概念一、线性回归的基本概念一、线性回归的基本概念一、线性回归的基本概念相关是分析两个正态变量X与Y之间的互相关系之间的互相关系之间的互相关系之间的互相关系。在相关分析中，分不清X与Y何者为自变量，何者为因变量何者为自变量，何者为因变量何者为自变量，何者为因变量何者为自变量，何者为因变量。现在假设两个变量X 、Y 中，当一个变量中，当一个变量中，当一个变量中，当一个变量X 改变时，另一个变量改变时，另一个变量改变时，另一个变量改变时，另一个变量 Y 也相应地改变，当这样的两个变量之间存在着直线关系时，也相应地改变，当这样的两个变量之间存在着直线关系时，也相应地改变，当这样的两个变量之间存在着直线关系时，也相应地改变，当这样的两个变量之间存在着直线关系时，不仅可以用相关系数不仅可以用相关系数不仅可以用相关系数不仅可以用相关系数 r 表示变量Y与X线性关系的密切程度，线性关系的密切程度，线性关系的密切程度，线性关系的密切程度，也可以用一个直线方程来表示 Y 与 X 的线性关系。根据大量实测数据，寻找出其规律性，寻求一个直线方程根据大量实测数据，寻找出其规律性，寻求一个直线方程根据大量实测数据，寻找出其规律性，寻求一个直线方程根据大量实测数据，寻找出其规律性，寻求一个直线方程来描述两个变量间依存变化的近似的线性数量关系，即线来描述两个变量间依存变化的近似的线性数量关系，即线来描述两个变量间依存变化的近似的线性数量关系，即线来描述两个变量间依存变化的近似的线性数量关系，即线性回归关系，这样得出的直线方程叫做性回归关系，这样得出的直线方程叫做性回归关系，这样得出的直线方程叫做性回归关系，这样得出的直线方程叫做线性回归方程。 31 目的：研究应变量Y对自变量X的数量依存关系。的数量依存关系。的数量依存关系。的数量依存关系。特点：统计关系。 X值和Y值均数的关系，不同于一般数学上的不同于一般数学上的不同于一般数学上的不同于一般数学上的X 和Y的函数关系 32 线性回归方程的形式为：其中是给定 X时Y的估计值 b 称为回归系数(regression coefficient)。 33 1．a 为回归直线在 Y 轴上的截距 (intercept) (intercept) (intercept) (intercept) � a > 0，表示直线与纵轴的交点在原点表示直线与纵轴的交点在原点表示直线与纵轴的交点在原点表示直线与纵轴的交点在原点的上方 � a 0，直线从左下方走向右上方，，直线从左下方走向右上方，，直线从左下方走向右上方，，直线从左下方走向右上方，Y 随 X 增大而增大； � b<0，直线从左上方走向右下方，，直线从左上方走向右下方，，直线从左上方走向右下方，，直线从左上方走向右下方，Y 随 X 增大而减小； � b=0，表示直线与 X 轴平行，X 与Y 无直线关系 b 的统计学意义是：X 每增加(减) 一个单位，Y 平均改变b个单位 35 二、线性回归方程的计算二、线性回归方程的计算二、线性回归方程的计算二、线性回归方程的计算例10.3 有人研究了温度对蛙的心率的影响，得到了表10-2中所示的资料，试进行回归分析。对象温度（X）心率（Y） XY X2 Y2 1 2 5 10 4 25 2 4 11 44 16 121 3 6 11 66 36 121 4 8 14 112 64 196 5 10 22 220 100 484 6 12 23 276 144 529 7 14 32 448 196 1024 8 16 29 464 256 841 9 18 32 576 324 1024 10 20 34 680 400 1156 11 22 33 726 484 1089 合计 132 246 3622 2024 6610 自变量？因变量？ 36

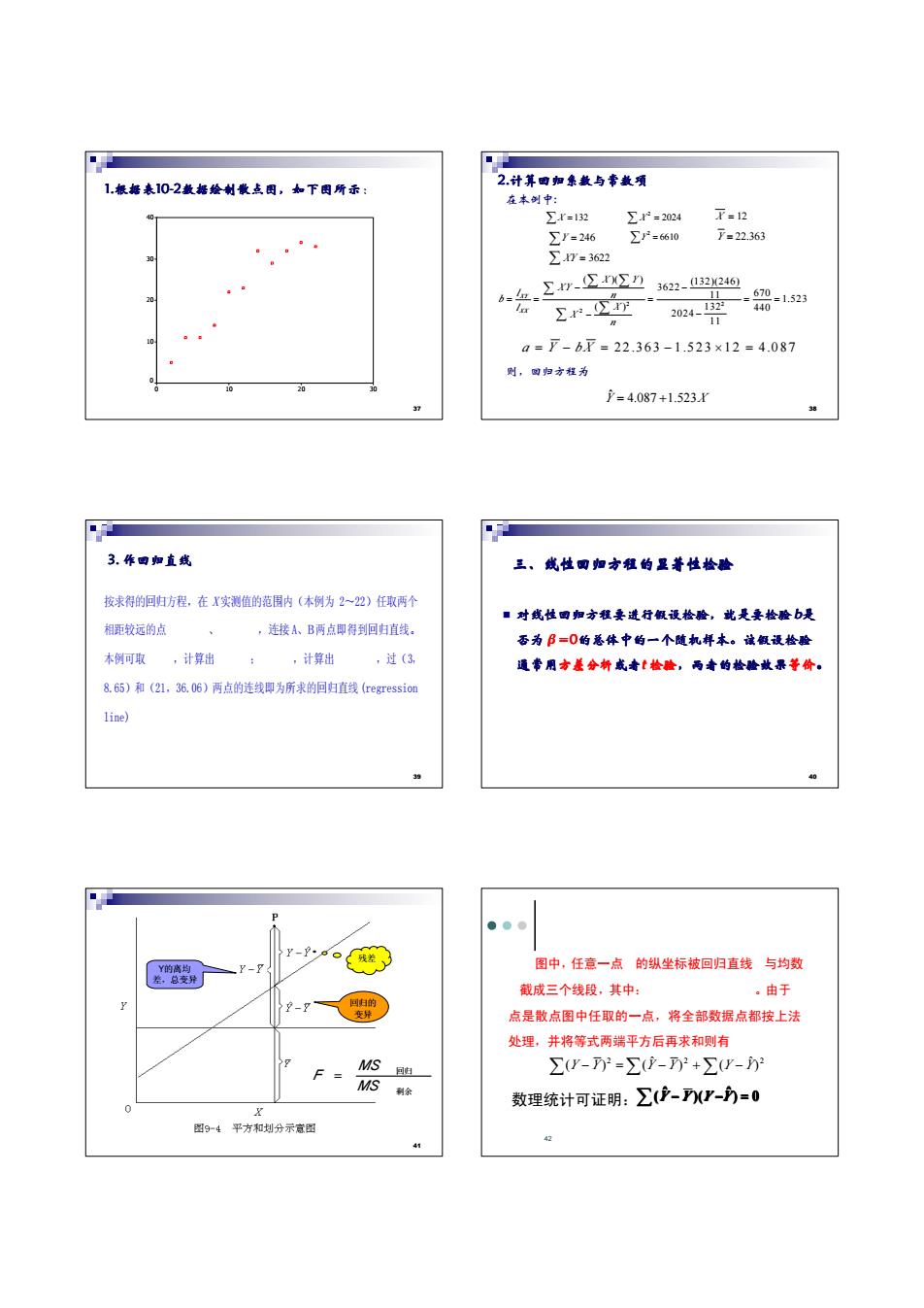
1.根据表10-2数据绘制散点图，如下图所示数据绘制散点图，如下图所示数据绘制散点图，如下图所示数据绘制散点图，如下图所示： 0 10 20 30 40 30 20 10 0 37 2.计算回归系数与常数项计算回归系数与常数项计算回归系数与常数项计算回归系数与常数项在本例中: ∑X = 132 ∑ = 2024 2 X X = 12 ∑Y = 246 2 ∑Y = 6610 Y = 22.363 ∑ XY = 3622 2 2 2 ( )( ) (132)(246) 3622 670 11 1.523 ( ) 132 440 2024 11 XYXX X Y XY l n b l X X n − − = = = = = − − ∑ ∑ ∑ ∑ ∑ a Y b X = − = − × = 2 2 .3 6 3 1 .5 2 3 1 2 4 .0 8 7 ˆY X = + 4.087 1.523 则，回归方程为 38 3. 作回归直线按求得的回归方程，在 X实测值的范围内（本例为 2～22）任取两个相距较远的点、，连接 A、B两点即得到回归直线。本例可取，计算出；，计算出，过（3， 8.65）和（21，36.06）两点的连线即为所求的回归直线 (regression line) 39 三、线性回归方程的显著性检验三、线性回归方程的显著性检验三、线性回归方程的显著性检验三、线性回归方程的显著性检验 � 对线性回归方程要进行假设检验，就是要检验对线性回归方程要进行假设检验，就是要检验对线性回归方程要进行假设检验，就是要检验对线性回归方程要进行假设检验，就是要检验b是否为β=0的总体中的一个随机样本。该假设检验的总体中的一个随机样本。该假设检验的总体中的一个随机样本。该假设检验的总体中的一个随机样本。该假设检验通常用方差分析或者t 检验，两者的检验效果，两者的检验效果，两者的检验效果，两者的检验效果等价。 40 Y的离均差，总变异残差回归的变异剩余回归 MS MS F = 41 图中，任意一点的纵坐标被回归直线与均数截成三个线段，其中：。由于点是散点图中任取的一点，将全部数据点都按上法处理，并将等式两端平方后再求和则有数理统计可证明： ∑ − =∑ − +∑ − 2 2 2 ) ˆ ) ( ˆ (Y Y ) (Y Y Y Y ) 0 ˆ )( ˆ ∑(Y −Y Y −Y = 42

上式用符号表示为式中即，为的离均差平方和，表示未考虑与的回归关系时的总变异。 43 即，为回归平方和。由于特定样本的均数 Y 是固定的，所以这部分变异由 ˆYi 的大小不同引起。当 X 被引入回归以后，正是由于 Xi 的不同导致了不同，所以 SS回反映了在 Y 的总变异中可以用 X 与 Y 的直线关系解释的那部分变异。 b 离 0 越远，X 对 Y 的影响越大，就越大，说明回归效果越好。 Y 44 即，为残差平方和。它反应除了对的线性影响之外的一切因素对的变异的作用，也就是在总平方和中无法用解释的部分，表示考虑回归之后真正的随机误差。在散点图中，各实测点离回归直线越近，也就越小，说明直线回归的估计误差越小，回归的作用越明显。上述三个平方和，各有其相应的自由度ν ，并有如下的关系：，，， 45 以上分解可见，不考虑回归时，随机误差是 Y 的总变异 S S 总；而考虑回归以后，由于回归的贡献使原来的随机误差减小为 S S 残。如果两变量间总体回归关系确实存在，回如果两变量间总体回归关系确实存在，回如果两变量间总体回归关系确实存在，回如果两变量间总体回归关系确实存在，回归的贡献就要大于随机误差，大到何种程度归的贡献就要大于随机误差，大到何种程度归的贡献就要大于随机误差，大到何种程度归的贡献就要大于随机误差，大到何种程度时可以认为具有统计意义，可计算统计量时可以认为具有统计意义，可计算统计量时可以认为具有统计意义，可计算统计量时可以认为具有统计意义，可计算统计量F: 46 M S 回为回归均方 M S 残为残差均方。 F 服从自由度为 ν ν 回、残的 F 分布。式中， xx xy yy xx xy xx l l SS SS SS l l l SS bl 2 2 = − = − = = 剩总回回 47 线性回归方程的显著性检验线性回归方程的显著性检验线性回归方程的显著性检验线性回归方程的显著性检验-方差分析 � 检验的基本思想检验的基本思想检验的基本思想检验的基本思想: 如果 X 与 Y 之间无线性回归关系，之间无线性回归关系，之间无线性回归关系，之间无线性回归关系，则 SS回归与 SS剩余都是其它随机因素对都是其它随机因素对都是其它随机因素对都是其它随机因素对Y的影响，由此描写变异的响，由此描写变异的响，由此描写变异的响，由此描写变异的 MS回归与 MS剩余应近似相等，总体回归系数，总体回归系数，总体回归系数，总体回归系数β=0，反之，β≠0。于是，可用 F 检验对 X 与 Y 之间有无回归关系进行检验。之间有无回归关系进行检验。之间有无回归关系进行检验。之间有无回归关系进行检验。 48

值的变异可用式来反映，而每个都可以分解成下式： ) ˆ ) ( ˆ Y − Y = (Y − Y + Y − Y 将此式两边平方然后展开，得： ∑ − =∑ − + − 2 2 Y Y ) ] ˆ Y ) ( Y ˆ (Y Y ) [ ( = ∑ − +∑ − + ∑ − Y −Y ) ˆ Y )( Y ˆ Y Y ) 2 ( ˆ Y ) ( Y ˆ ( 2 2 其中则： 49 回归系数的假设检验可用下面简化公式计算 ∑ ∑ = ∑ − = − nY SS Y Y Y 2 2 2 ( ) ( ) 总 =∑ − = ∑ + − − = ∑ − 2 2 2 2 Y Y ) (Y b( X X ) Y ) b ( X X ) ˆ SS回归 ( XX XY 2 XX XY XX XY L L L bL L L = b = = SS 剩余= SS 总－SS 回归这三个平方和的自由度依次为：总=n－1, 回归=1, 剩余=n－2 50 回归回归回归 ν = SS MS 剩余剩余剩余 ν = SS MS 剩余回归 MS MS F = 51 对例10.3的回归方程用方差分析进行假设检验的回归方程用方差分析进行假设检验的回归方程用方差分析进行假设检验的回归方程用方差分析进行假设检验（1）建立假设检验）建立假设检验）建立假设检验）建立假设检验 β=0 β≠0 α=0.05 （2）计算统计量 SS总 SS回归 SS剩余= SS总－SS回归=88.31 2 2 2 ( ) 246 6610 1108.54 11 Y Y n = − = − = ∑ ∑ 1020.23 440 670 2 2 = = = XX XY l l / 1020.23/1 103.97 / 88.31/9 MS SS F MS SS ν ν = = = = 回归回归回归剩余剩余剩余 52 （3）确定P值得出统计结论值得出统计结论值得出统计结论值得出统计结论查F界值表， V回归 = 1, V剩余 = 9，按照a=0.05的检验水准，拒绝的检验水准，拒绝的检验水准，拒绝的检验水准，拒绝H0 ，接受H1，可以认为温度与蛙的心率之间存在线性回归关系。度与蛙的心率之间存在线性回归关系。度与蛙的心率之间存在线性回归关系。度与蛙的心率之间存在线性回归关系。 0.01(1, 9) F = 10.56 F F > 0.01(1, 9) P < 0.01 53 方差分析表变异来源 SS ν MS F P 总变异 1108.54 10 回归 1020.23 1 1020.23 103.97 < 0.01 剩余 88.31 9 9.81 54

对例10.3的回归方程用t 检验进行假设检验（1）建立假设检验 β=0 β≠0 α=0.05 （2）计算统计量 88.31 3.13 9 Y X s ⋅ = = 3.13 0.149 440 b s = = 1.523 0 10.22 0.149 t − = = V =11－2=9 （3）确定P值作结论根据 V =9， 0.01/ 2 (9 ) t = 3.250, P <0.01，拒绝H0，结论与F 检验相同。 F = t 103.97 10.22 ≈ 55 注意：，即直线回归中对回归系数的检验与检验等价，类似于两样本均数比较可以作检验亦可作方差分析。 56 四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项 ⒈ 只有将两个内在有联系的变量放在一起进行回归分析才是有只有将两个内在有联系的变量放在一起进行回归分析才是有只有将两个内在有联系的变量放在一起进行回归分析才是有只有将两个内在有联系的变量放在一起进行回归分析才是有意义的。 ⒉ 作回归分析时，如果两个有内在联系的变量之间存在的是一作回归分析时，如果两个有内在联系的变量之间存在的是一作回归分析时，如果两个有内在联系的变量之间存在的是一作回归分析时，如果两个有内在联系的变量之间存在的是一种依存因果的关系，那么应该以种依存因果的关系，那么应该以种依存因果的关系，那么应该以种依存因果的关系，那么应该以“因”的变量为X ,以“果” 的变量为Y 。如果变量之间并无因果关系，则应。如果变量之间并无因果关系，则应。如果变量之间并无因果关系，则应。如果变量之间并无因果关系，则应以易于测定、较为稳定或变异较小者为较为稳定或变异较小者为较为稳定或变异较小者为较为稳定或变异较小者为X 。 ⒊ 在回归分析中，在回归分析中，在回归分析中，在回归分析中，因变量是随机变量因变量是随机变量因变量是随机变量因变量是随机变量，自变量既可以是随机变，自变量既可以是随机变，自变量既可以是随机变，自变量既可以是随机变量（II型回归模型，两个变量应该都服从正态分布），也可型回归模型，两个变量应该都服从正态分布），也可型回归模型，两个变量应该都服从正态分布），也可型回归模型，两个变量应该都服从正态分布），也可以是给定的量（以是给定的量（以是给定的量（以是给定的量（I型回归模型，这时，与每个型回归模型，这时，与每个型回归模型，这时，与每个型回归模型，这时，与每个X 取值相对应的变量Y必须服从正态分布必须服从正态分布必须服从正态分布必须服从正态分布），如果数据不符合要求，在进行），如果数据不符合要求，在进行），如果数据不符合要求，在进行），如果数据不符合要求，在进行回归分析前，必须先进行变量的变换。回归分析前，必须先进行变量的变换。回归分析前，必须先进行变量的变换。回归分析前，必须先进行变量的变换。 57 四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项四、进行线性回归分析的注意事项 ⒋ 回归方程建立后必须作假设检验，只有经假设检回归方程建立后必须作假设检验，只有经假设检回归方程建立后必须作假设检验，只有经假设检回归方程建立后必须作假设检验，只有经假设检验拒绝了无效假设，回归方程才有意义。验拒绝了无效假设，回归方程才有意义。验拒绝了无效假设，回归方程才有意义。验拒绝了无效假设，回归方程才有意义。 ⒌ 使用回归方程计算估计值时，不可把估计的范围使用回归方程计算估计值时，不可把估计的范围使用回归方程计算估计值时，不可把估计的范围使用回归方程计算估计值时，不可把估计的范围扩大到建立方程时的自变量的取值范围之外。扩大到建立方程时的自变量的取值范围之外。扩大到建立方程时的自变量的取值范围之外。扩大到建立方程时的自变量的取值范围之外。 58 第三节线性相关和回归的区别与联系线性相关和回归的区别与联系线性相关和回归的区别与联系线性相关和回归的区别与联系 59 一、线性相关与回归的区别一、线性相关与回归的区别一、线性相关与回归的区别一、线性相关与回归的区别 ⒈ 相关系数的计算只适用于两个变量都服从正相关系数的计算只适用于两个变量都服从正相关系数的计算只适用于两个变量都服从正相关系数的计算只适用于两个变量都服从正态分布的情形，而在回归分析中，因变量是随态分布的情形，而在回归分析中，因变量是随态分布的情形，而在回归分析中，因变量是随态分布的情形，而在回归分析中，因变量是随机变量，自变量既可以是随机变量（机变量，自变量既可以是随机变量（机变量，自变量既可以是随机变量（机变量，自变量既可以是随机变量（II型回归模型，两个变量都应该服从正态分布），也可模型，两个变量都应该服从正态分布），也可模型，两个变量都应该服从正态分布），也可模型，两个变量都应该服从正态分布），也可以是给定的量（以是给定的量（以是给定的量（以是给定的量（I型回归模型，这时，与每个型回归模型，这时，与每个型回归模型，这时，与每个型回归模型，这时，与每个X 取值相对应的变量取值相对应的变量取值相对应的变量取值相对应的变量Y必须服从正态分布必须服从正态分布必须服从正态分布必须服从正态分布）。 ⒉ 线性相关表示两个变量之间的线性相关表示两个变量之间的线性相关表示两个变量之间的线性相关表示两个变量之间的相互关系是双向的，回归则反映两个变量之间的，回归则反映两个变量之间的，回归则反映两个变量之间的，回归则反映两个变量之间的依存关系，是单向的。 60

石河子大学：《医学统计学》课程教学课件（非预防专业）第10章 线性相关与回归

石河子大学：《医学统计学》课程教学课件（非预防专业）第10章线性相关与回归