
第三章方差分析 引 言

第三章方差分析 第一节方差分析的基本原理 第二节完全随机设计试验结果的方差分析 第三节随机区组设计试验结果的方差分析 第四节拉丁方设计试验结果的方差分析 第五节裂区设计试验结果的方差分析 第六节多年多点试验结果的方差分析 第七节方差分析中一些应注意的问题
第一节方差分析的基本原理 基本原理 SS与DF 数学模型及 的分解 F测验 多重比较 期望均方
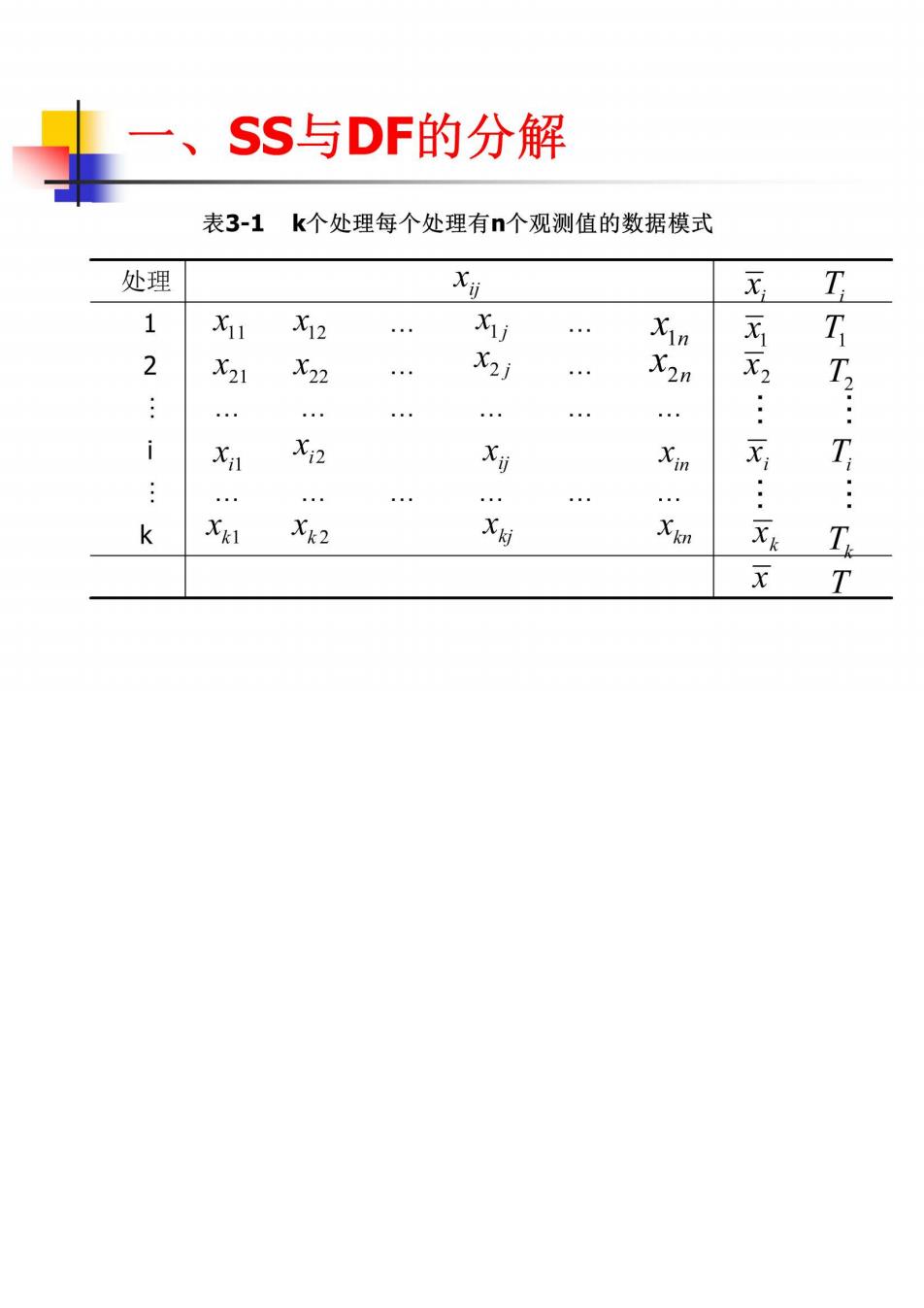
一、 SS与DF的分解 表3-1k个处理每个处理有n个观测值的数据模式 处理 T X12 … … Xin 元1 T 2 X21 X22 X2j n x, i N Xi2 Xin x T XkI Xk2 T x

二、F测验 (一)方法步骤(右尾测验) 第一步提出假设H。:o2≤o2;H4:o2fo,2 第二步确定显著水平 第三步计算概率 F=52 第四步推断 (二)注意项 1.求F时的分子、分母 2.F测验显著与否

例 【例3-1】有一水稻施肥的盆栽试验,设5个处理,A 和B系分别施用两种不同工艺流程的氨水,C施碳 酸氢铵,D施尿素,E不施肥。每处理4盆,共20 盆,随机置于同一网室中,其稻谷产量列于下表。 试测验各处理平均数的差异显著性
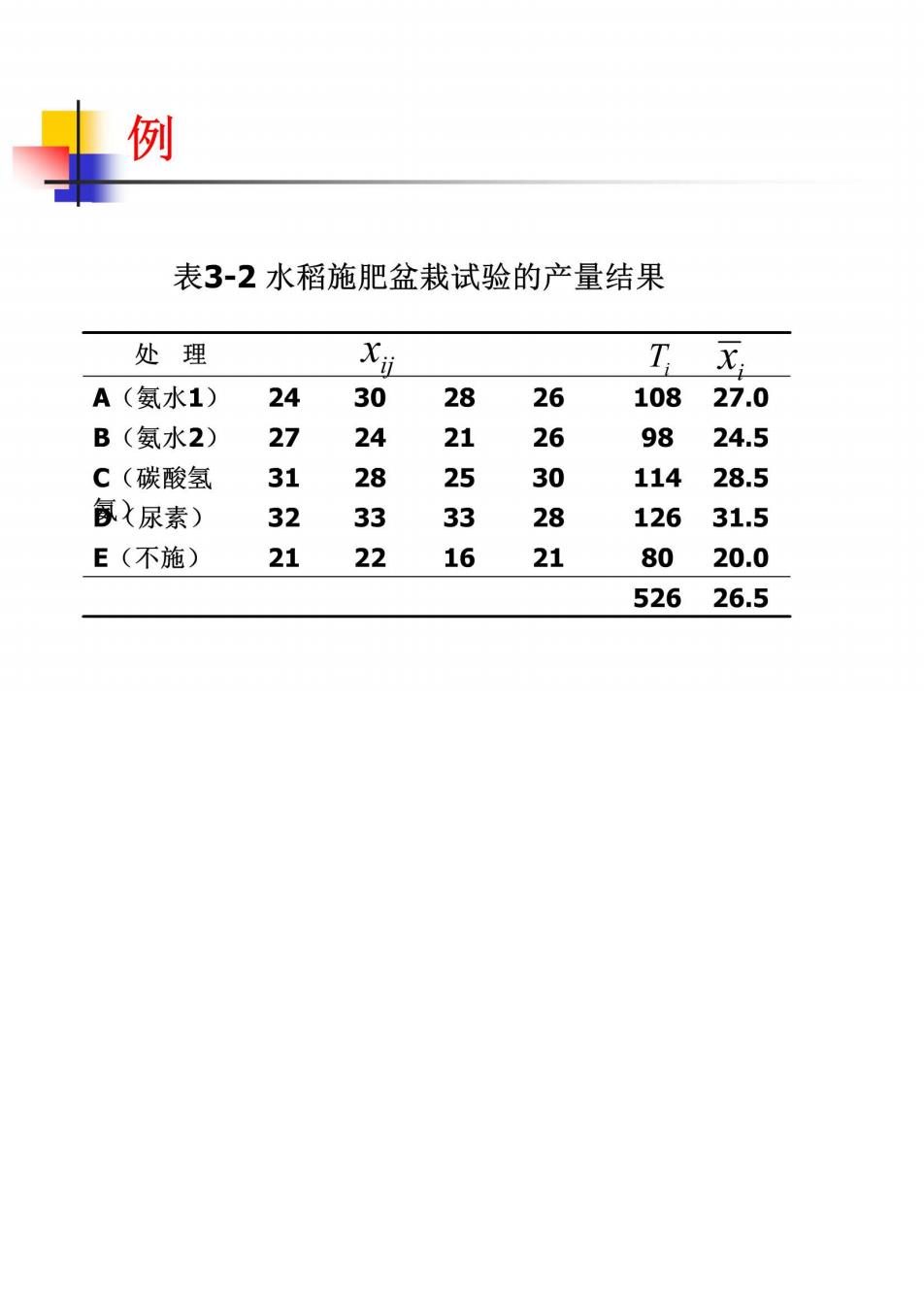
例 表3-2水稻施肥盆栽试验的产量结果 处理 Xi T x. A(氨水1) 24 30 28 26 10827.0 B(氨水2) 27 24 21 26 98 24.5 C(碳酸氢 31 28 25 30 11428.5 每X尿素) 32 33 33 28 12631.5 E(不施) 21 22 16 21 8020.0 52626.5
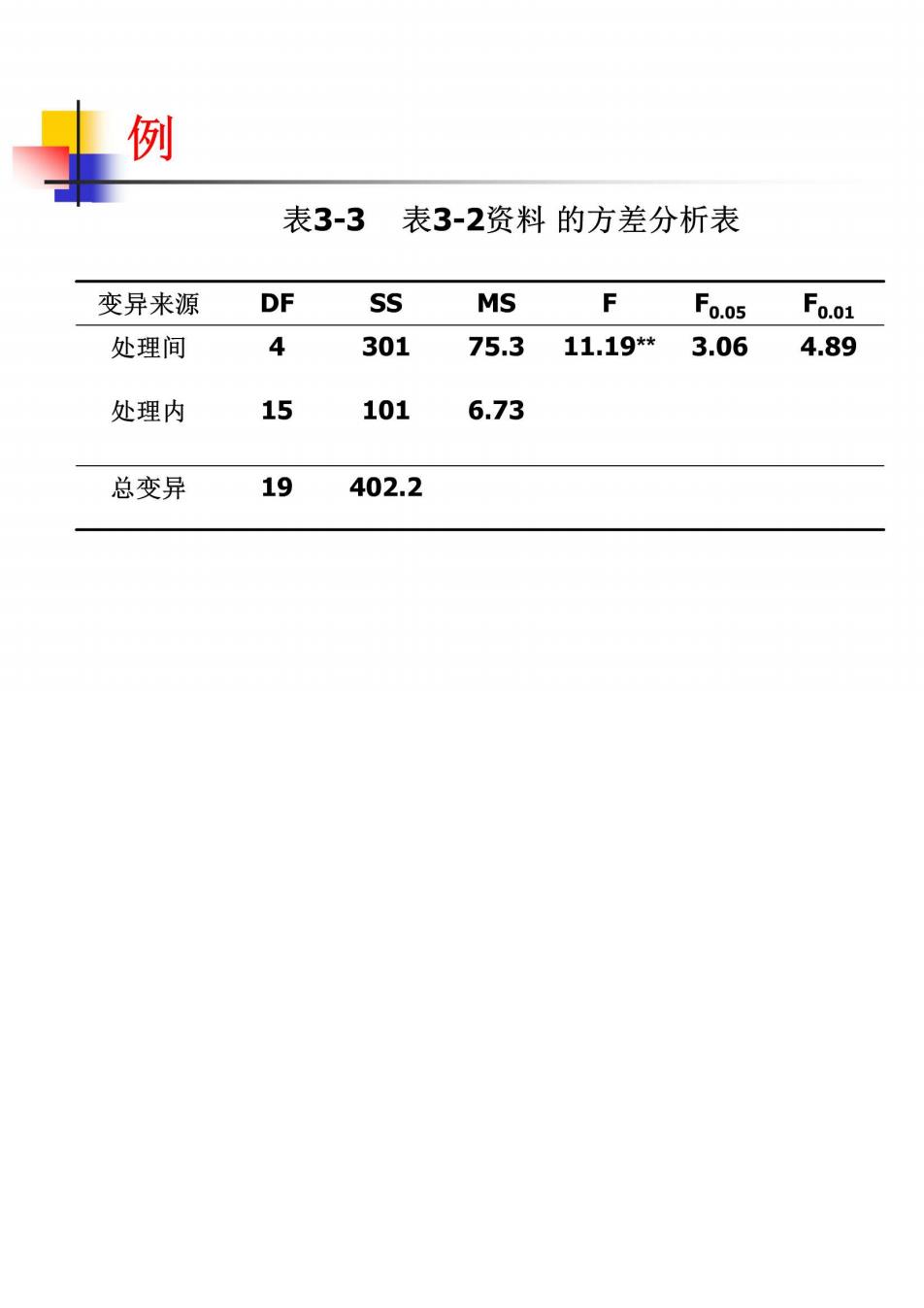
例 表3-3表3-2资料的方差分析表 变异来源DF SS MS Fo.05F0.01 处理间 4 30175.311.19*3.064.89 处理内 15 101 6.73 总变异 19 402.2

三、多重比较 (一)概念 (二)方法 1.最小显著差数法(LSD法) 2.最小显著极差法(LSR法) (1)SSR法 (2)q法 (三)应用条件

最小显著差数法的步骤 第一步求平均数差数标准误5=、 22 第二步查表得临界tav 第三步求最小显著差数值LSD。=S-×t。 第四步处理间差异比较