电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第18讲 电抗网络综合（电抗梯形滤波器综合）

第18讲电抗梯形滤波器综合 第九章：电抗梯形滤波器综合（2) 9-2和9-5两节。 第9章内容：第17-18讲

第18讲 电抗梯形滤波器综合 第九章:电抗梯形滤波器综合（2） 9-2和9-5两节。 第9章内容：第17-18讲

电抗网络的极点移出和部分极点移出运算(9.2) 无源滤波器综合方法： 1、福斯特 2、考尔 3、? 极点移出和部分极点移出

无源滤波器综合方法： 1、福斯特 2、考尔 3、？ 极点移出和部分极点移出 电抗网络的极点移出和部分极点移出运算(9.2)

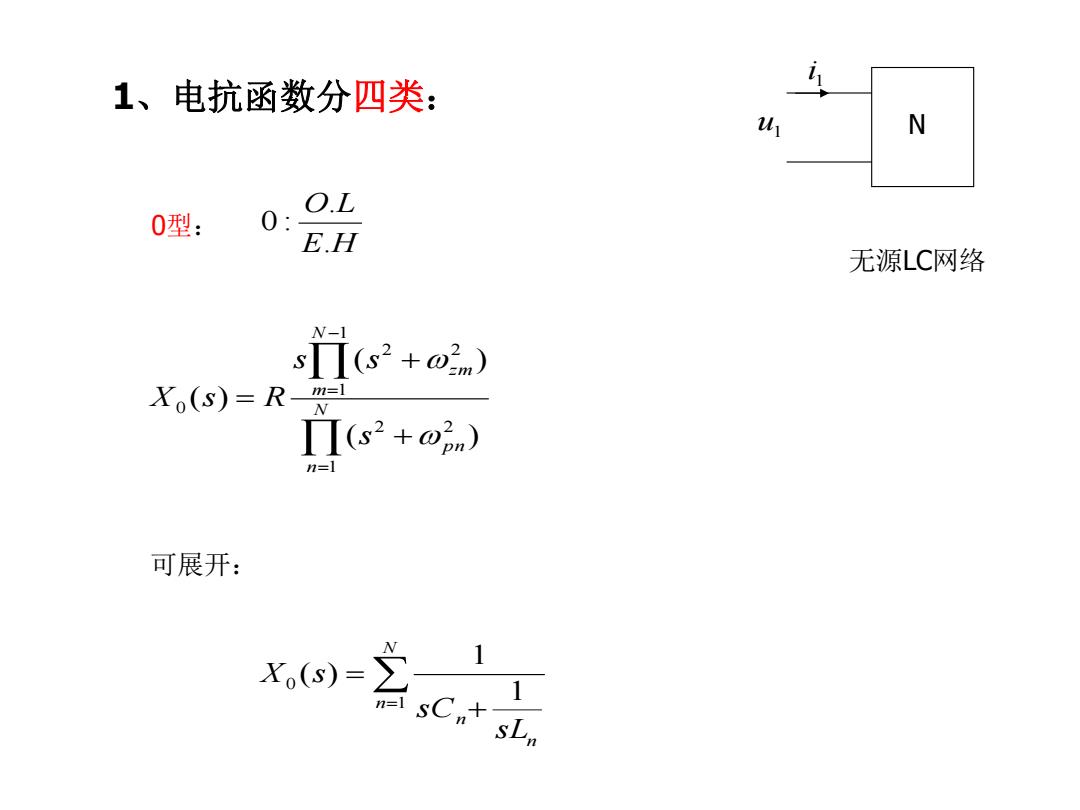
1、电抗函数分四类： 1 N O.L 0型： 0: EH 无源LC网络 W-1 sΠ(s2+o2m) Xo(s)=Rm旦 Π(s2+o2n) 可展开： X(s)= 1 sL

0型： u1 1 i N 无源LC网络         N n p n N m zm s s s X s R 1 2 2 1 1 2 2 0 ( ) ( ) ( )   E H O L . . 0 : 1、电抗函数分四类：    N n n n sL sC X s 1 0 1 1 ( ) 可展开：

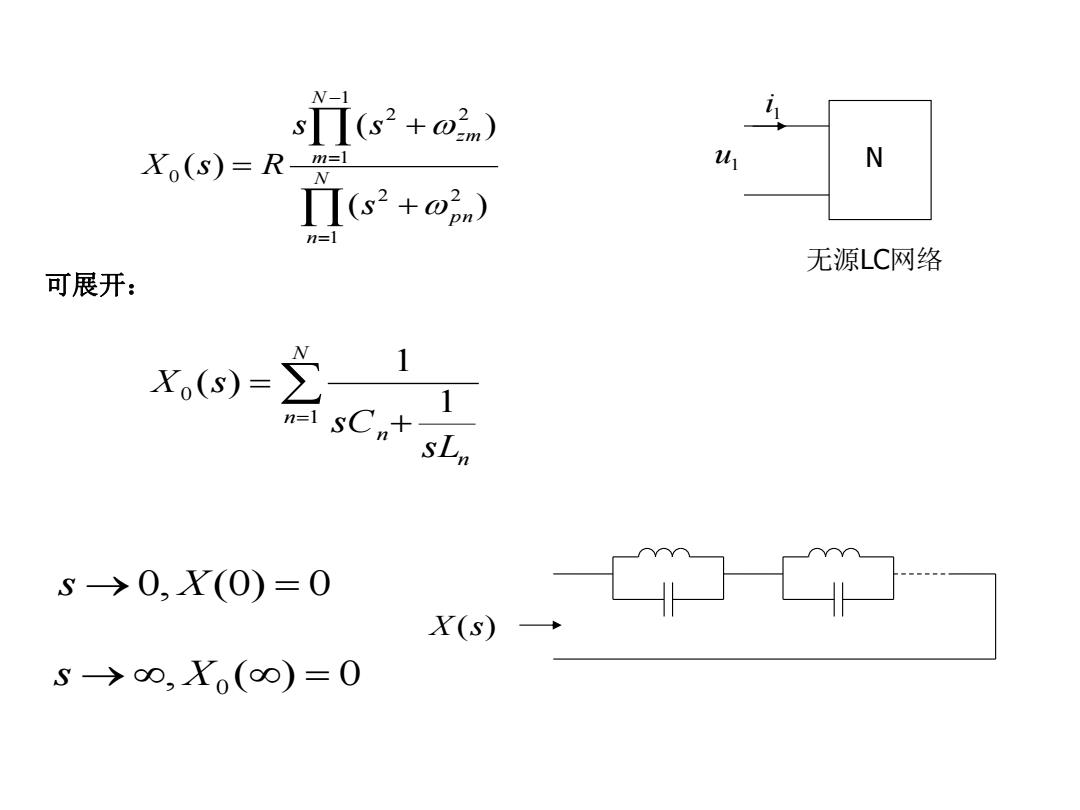
N-1 s(s2+o2nm)） Xo(s)=R-m=1 N Π(s2+o2n) 无源LC网络 可展开： X()=∑ S>0,X(0)=0 X(s) 5>∞，Xo(0)=0

u 1 1 i N 无源LC网络    Nn p n Nm zm s s s X s R 1 2 2 11 2 2 0 ( ) ( ) ( )     Nn n n sL sC X s 1 0 1 1 ( ) 可展开： s  0 , X ( 0 )  0 s   , X0 (  )  0 X ( s )

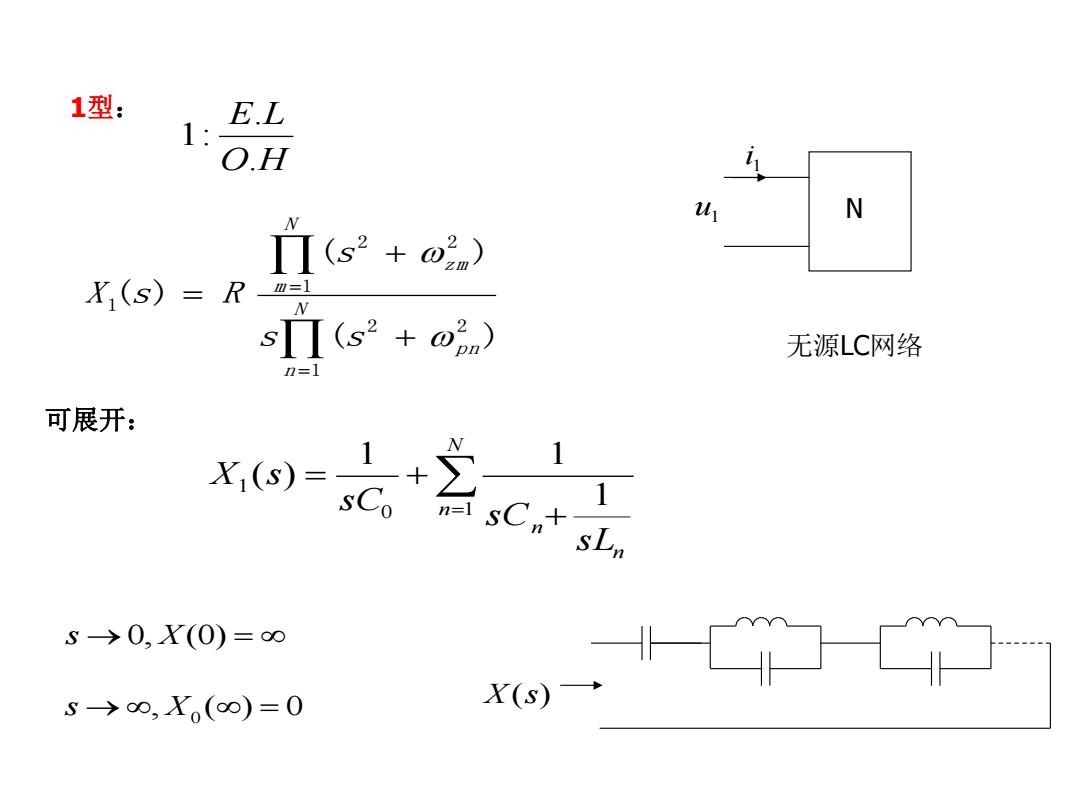
1型： E.L 1: O.H N Π(s2+o2m) Y(s)=R=1 sΠ(s2+o3) 无源LC网络 n= 可展开： n=1 sC sL. S>0,X(0)=∞ .白的 S-→∞，X(∞)=0 X(s)

1 型 ： u 1 1 i N  无源LC网络    N n p n N m z m s s s X s R 1 2 2 1 2 2 1 ( ) ( ) ( )   O H E L . . 1 :     Nn n n sL sC sC X s 0 1 1 1 1 1 ( ) 可展开： s  0 , X ( 0 )   s   , X0 (  )  0 X ( s )

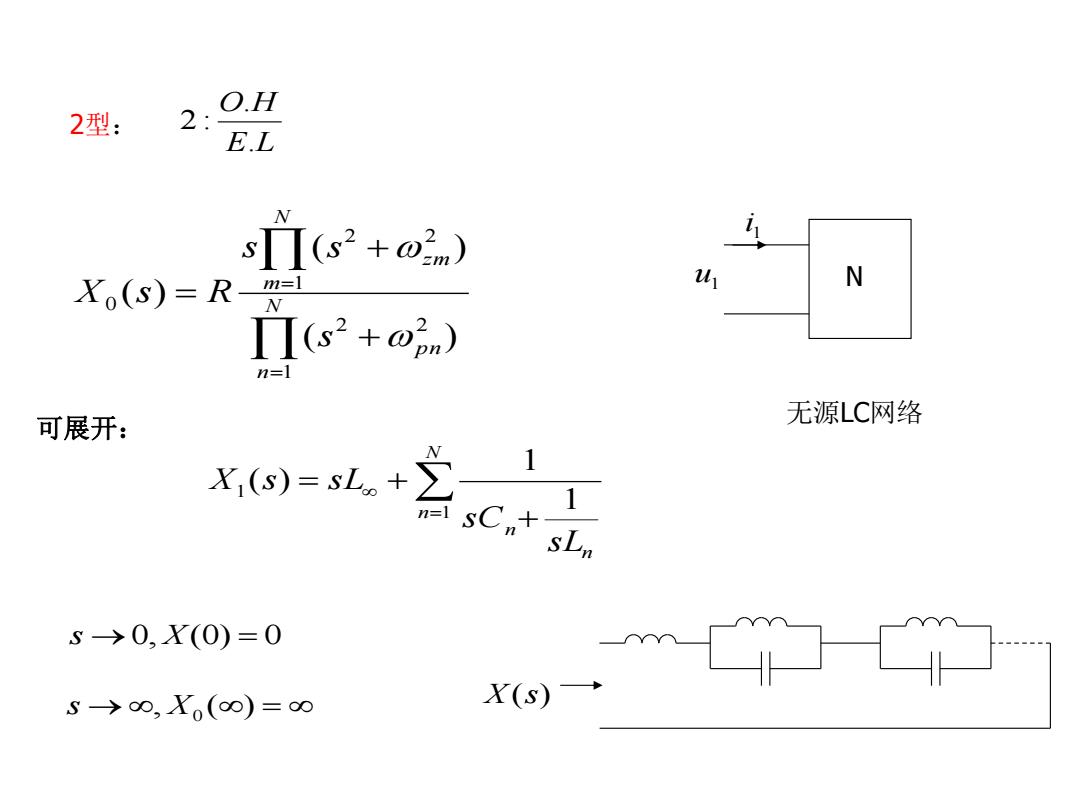
O.H 2型： 2: E.L sΠ(s2+om) Xo(S)=R-m=1 W小 N Π(s2+o2m) 可展开： 无源LC网络 r0-+c sL. S>0,X(0)=0 S→0，X0(∞)=∞ X(s)

2 型 ： u 1 1 i N 无源LC网络    Nn p n Nm z m s s s X s R 1 2 2 1 2 2 0 ( ) ( ) ( )  E L O H. . 2 :      Nn n n sL sC X s sL 1 1 1 1 ( ) 可展开： s  0 , X ( 0 )  0 s   , X0 (  )   X ( s )

E.H 3型： 3: O.L Π(s2+o2m) Xo(S)=Rm是 41 N N- sΠ(s2+om) n三 可展开： 无源LC网络 n=1 S>0,X(0)=∞ .门 S→0，Xo(∞)=0 Y(s)

3型： u1 1 i N 无源LC网络         1 1 2 2 1 2 2 0 ( ) ( ) ( ) N n p n N m zm s s s X s R   O L E H . . 3:       N n n n sL sC sC X s sL 0 1 1 1 1 1 ( ) 可展开： s 0, X(0)   s , X0 ()   X(s)

分子、分母的奇偶性，决定s=0处零、极点。 E Os=0,X(s)=∞ E,s=0,X(s)=0 分子、分母的方次高低，决定s=∞处零、极点。 元，s=0,X()=0 H L ,s=0,X(s)=0

,s  0, X (s)   O E ,s  0, X (s)  0 E O 分子、分母的奇偶性，决定s=0处零、极点。 ,s  , X(s)   L H ,s  , X (s)  0 H L 分子、分母的方次高低，决定s=∞处零、极点

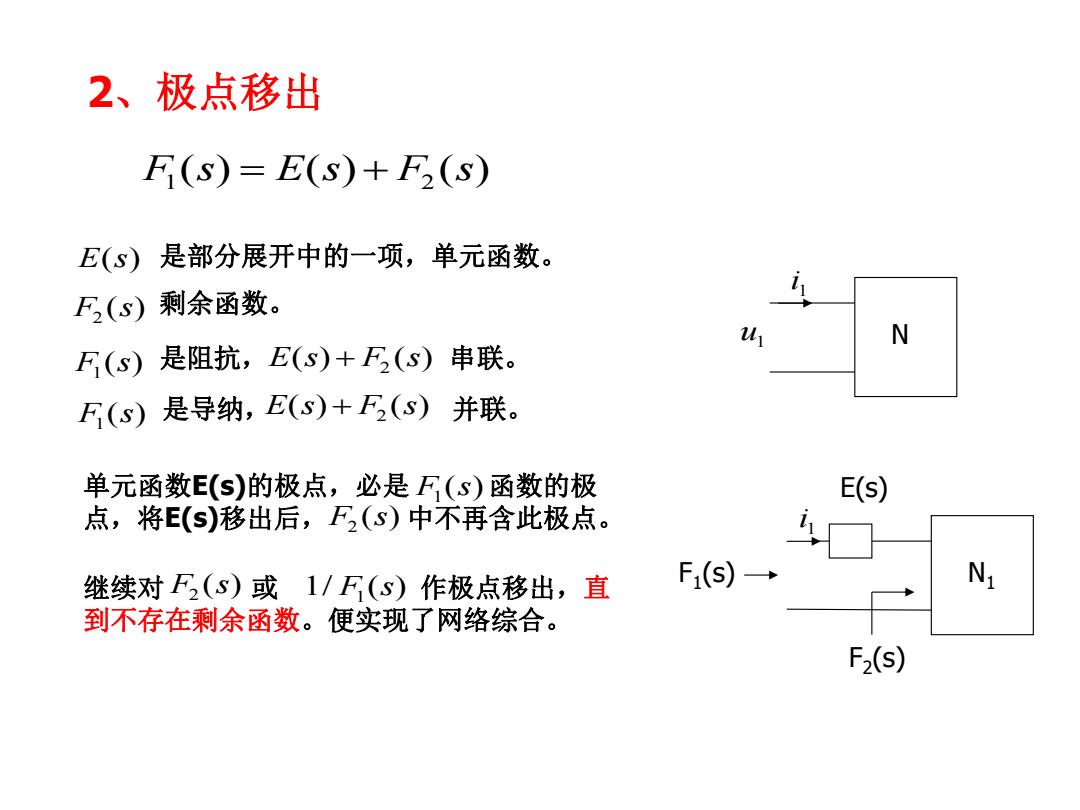
2、极点移出 F(S)=E(S)+F(S) E(s)是部分展开中的一项，单元函数。 F,(s)剩余函数。 N F(s)是阻抗，E(s)+F(s)串联。 F(s)是导纳，E(s)+F(s)并联。 单元函数E(s)的极点，必是F(s)函数的极 E(s) 点，将E(S)移出后，F(S)中不再含此极点。 继续对F(S)或1/F(S)作极点移出，直 F(S)→ N 到不存在剩余函数。便实现了网络综合。 F2(s)

2、极点移出 u1 1 i N E(s) ( ) ( ) ( ) 1 2 F s  E s  F s ( ) 1 F s 是部分展开中的一项，单元函数。 1 i N1 E(s) F2 (s) F1 (s) ( ) 2 F s 剩余函数。 ( ) 1 F s 是阻抗， 串联。 ( ) 1 F s 是导纳， 并联。 ( ) ( ) 2 E s  F s ( ) ( ) 2 E s  F s 单元函数E(s)的极点，必是 函数的极 点，将E(s)移出后， F2 (s) 中不再含此极点。 继续对 或 作极点移出，直 到不存在剩余函数。便实现了网络综合。 ( ) 2 F s 1/ ( ) 1 F s

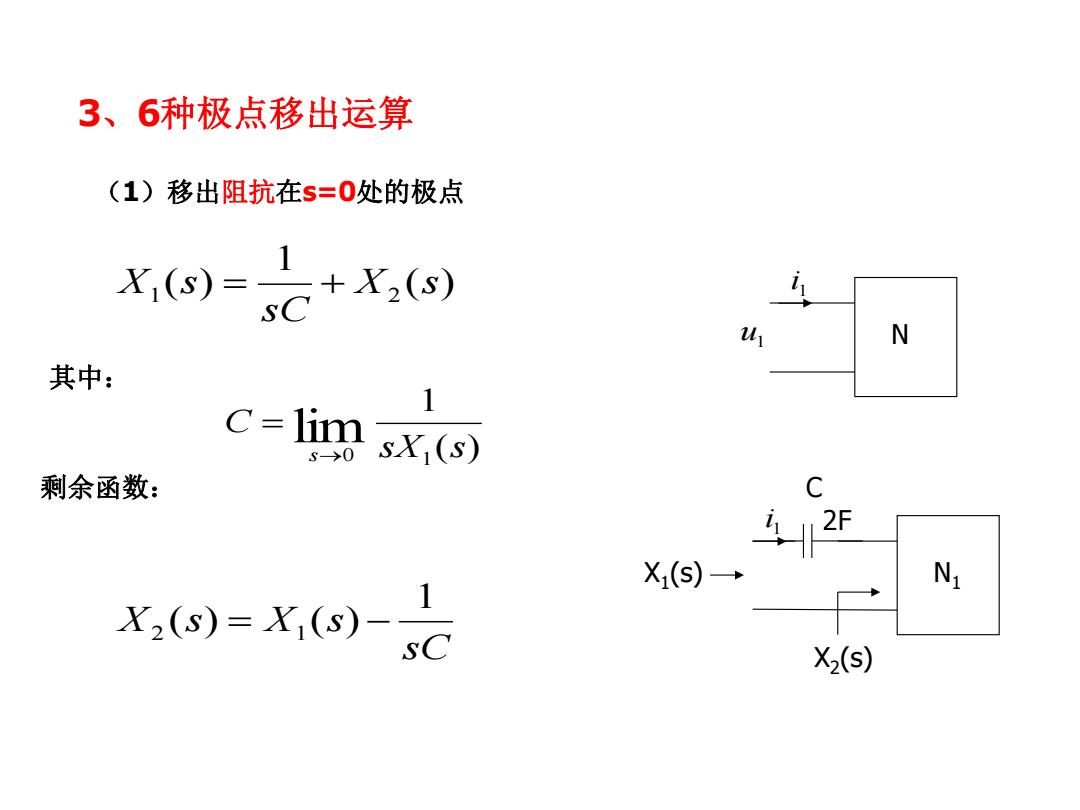
3、6种极点移出运算 (1)移出阻抗在s=0处的极点 xo)=C+x,() u N 其中： C-ling (s) 剩余函数： C 2F X(S)→ N Y2(s=X,(s)-1 X2(S)

3、6种极点移出运算 u1 1 i N ( ) 1 0 1 lim sX s C s  ( ) 1 ( ) 1 2 X s sC X s   sC X s X s 1 ( ) ( ) 2  1  其中： （1）移出阻抗在s=0处的极点 剩余函数： 1 i N1 C X2 (s) X1 (s) 2F