电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第13讲 无源网络综合基础

第13讲无源网络综合基础

第13讲 无源网络综合基础

7-4、电抗函数 7-4-1、电抗函数的基本性质 Zic(s)= s(s2+o31)(s2+o22). (s2+ω21(s2+032) 2c(s）=Ks+os2+w2). s(s2+ω21)(s2+o22） 对其部分分式展开，可得： Zc(0-K.s+9+g2+o+g2+o++g+@ 十 2

2 2 2 2 2 2 2 1 2 0 1 ( ) ... p n n p p LC s K s s K s s K s s K Z s K s             对其部分分式展开，可得： ( )( )... ( )( )... ( ) ( )( )... ( )( )... ( ) 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 p p z z LC p p z z LC s s s s s Z s K s s s s s Z s K                   7-4、电抗函数 7-4-1、电抗函数的基本性质

电抗函数的零、极点在虚轴上的分布规律 Zic(jo)=MK @-Ko K10 Kn +02-2 ++ 2=X(ω) pn 对X(o)求导。有： -K++云品 do 有： dx(@)-0 dw i dX(o）=Km≥0 →0 0

( ) [ ... ( ) 2 2 2 1 2 0 1           jX K K K Z j j K p n n p LC          电抗函数的零、极点在虚轴上的分布规律 0 ( )    d dX 0 ( ) lim     K dX    对X(ω)求导。有：       n i p K Ki K d dX 1 2 1 2 2 0 ( ) (       有：

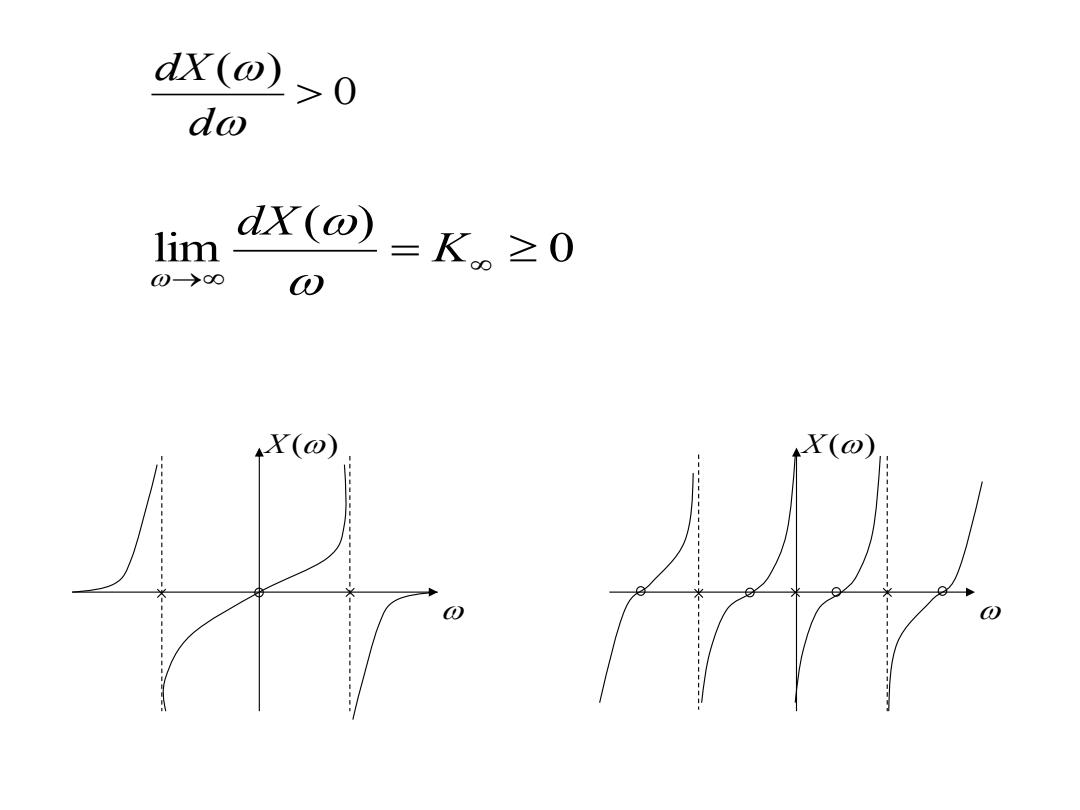
dX(w）>0 dw lim dX(o）=K≥0 0→∞ X(⊙) X(⊙) 0 11111 !

0 ( )    d dX 0 ( ) lim     K dX    X()  X() 

因此电抗函数有：（第261页) (1)F(s)是奇函数，奇函数与偶函数之比； (2)分子分母差一阶： (3)全部零、极点是单阶； (4)在原点和无穷远处，必有单阶极点或单阶零 点； (5)对于任何w,Fc(jO)为纯虚数； (6)X(ω)是严格单调增函数，其极点和零点在 ω轴上交替排列

因此电抗函数有：（第261页） （1）F(s)是奇函数，奇函数与偶函数之比； （2）分子分母差一阶； （3）全部零、极点是单阶； （4）在原点和无穷远处，必有单阶极点或单阶零 点； （5）对于任何ω，FLC(j ω)为纯虚数； （6）X(ω)是严格单调增函数，其极点和零点在 ω轴上交替排列

定理7-3：一个有理函数F(s)是LC网络 策动点函数的充分必要条件是： (1)F(s)的全部极点和零点在jω轴上交 替排列的单阶极点和单阶零点； (2)在s=0和s→∞处，F(s)必有单阶 极点或单阶零点

定理7-3：一个有理函数F(s)是LC网络 策动点函数的充分必要条件是： （1）F(s)的全部极点和零点在jω轴上交 替排列的单阶极点和单阶零点； （2）在s=0和s→∞处，F(s)必有单阶 极点或单阶零点

例（第286页) 判断以下函数的类型： 正实函数？LC函数？。。。。 1.Fs= s3+10s2+24s s2+7s+10 s4+4s2+3 2.F(s)= s5+6s3+8s

例（第286页） 判断以下函数的类型： 正实函数？LC函数？。。。。 3 2 2 10 24 1 7 10 4 6 2 5 s s s .F( s ) s s s( s )( s ) ( s )( s )           4 2 5 3 4 3 2 6 8 s s .F( s ) s s s     

例（第286页) 1.F)=s+10s2+245 s2+7s+10 s(s+4)(S+6 正实函数 (s+2)(s+5) s4+4s2+3 2.F(s)= s5+6s3+8s (s2+1)(s2+3) S(s2+2(s2+4 电抗函数

例（第286页） 电抗函数 正实函数 3 2 2 10 24 1 7 10 4 6 2 5 s s s .F( s ) s s s( s )( s ) ( s )( s )           3 2 2 10 24 7 10 4 6 2 5 s s s F( s ) s s s( s )( s ) ( s )( s )           4 2 5 3 4 3 2 6 8 s s .F( s ) s s s      2 2 2 2 1 3 2 4 ( s )( s ) s( s )( s )     

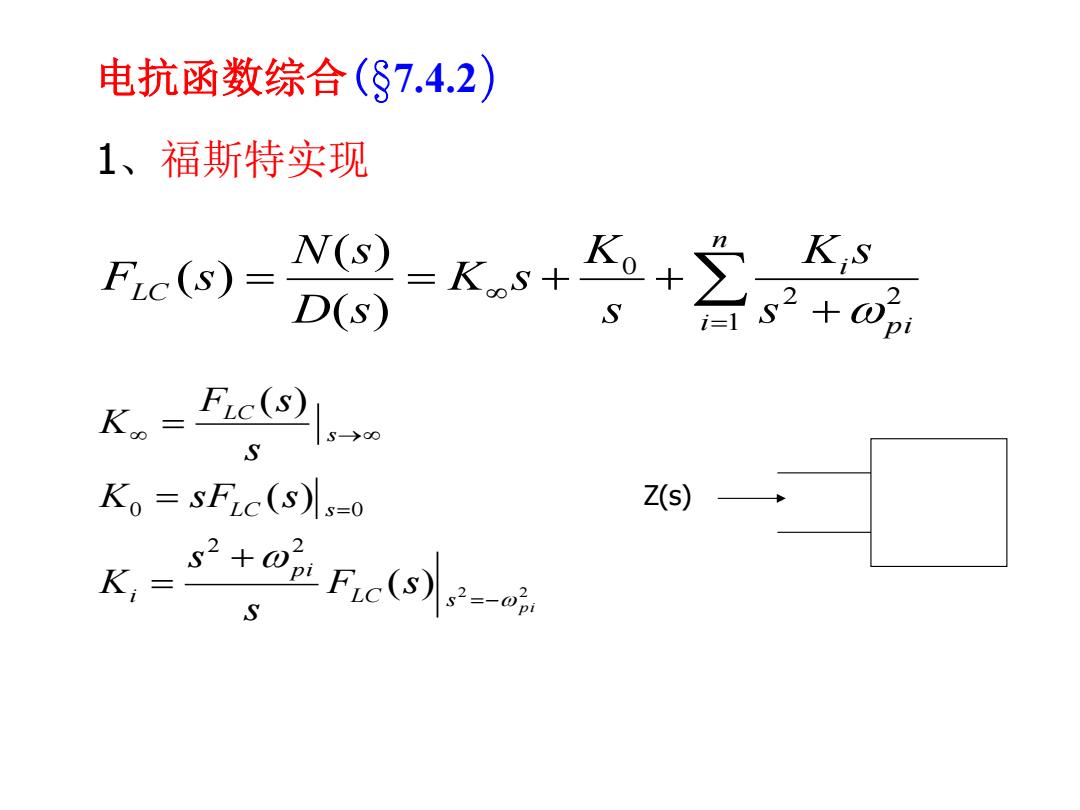
电抗函数综合(S7.4.2) 1、福斯特实现 Fu( 》K+会o K. Ko=sFLc(s)s-0 Z(s) k+吃F-

( ) 2 2 ( ) ( ) 2 2 0 0 p i LC s p i i LC s s LC F s s s K K sF s s F s K           电抗函数综合(i7.4.2) 1、福斯特实现        n i p i i LC s K s s K K s D s N s F s 1 2 2 0 ( ) ( ) ( )  Z(s)

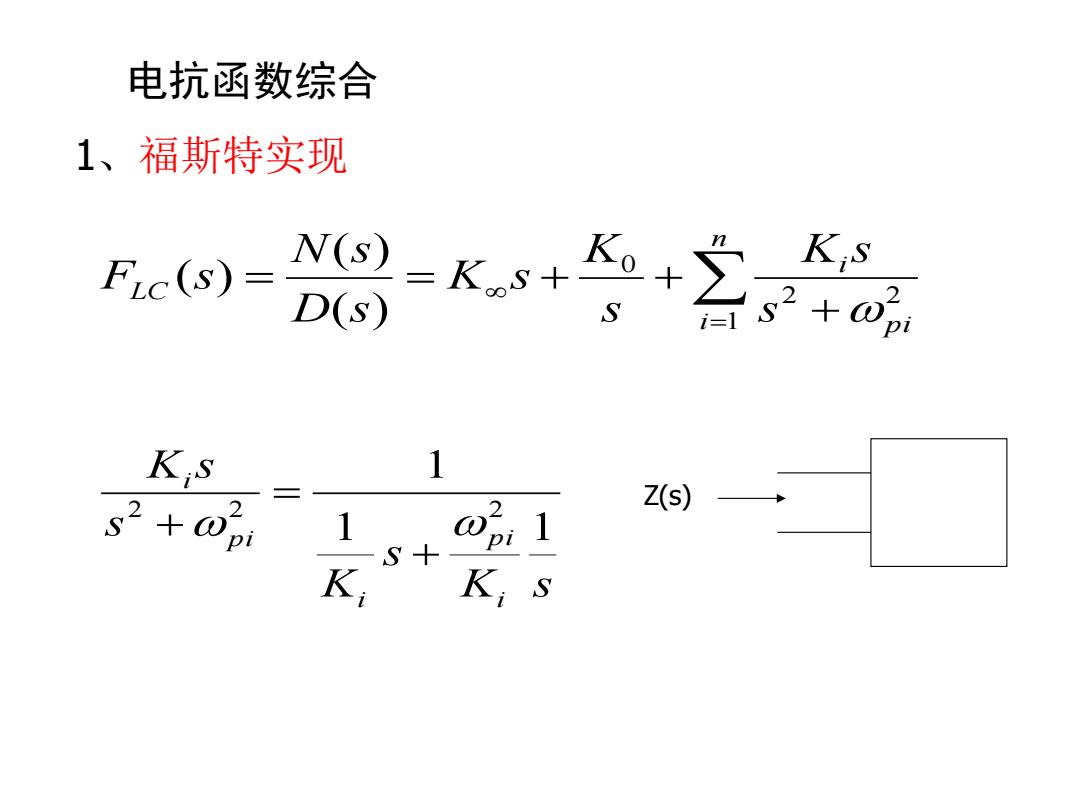
电抗函数综合 1、福斯特实现 Fc() -长鸟+李不a D(s) K;S 1 s2+02 Z(s) 1 -S十 K K;S

电抗函数综合 1、福斯特实现        n i p i i LC s K s s K K s D s N s F s 1 2 2 0 ( ) ( ) ( )  K s s K s K s i p i i p i i 1 1 1 2 2 2      Z(s)