
第9讲信号流图分析法
第9讲 信号流图分析法

一、信号流图的表达 信息流 载体,信息流动,必借助载体的流动; 电流,是信息流动的一种载体; 变量,数学符号。 y=ax +bx2 .a Z Z=Cy C X2 反映一种因果关系
一、信号流图的表达 z cy y ax bx 1 2 x2 x1 c a b y z 信息流 载体,信息流动,必借助载体的流动; 电流,是信息流动的一种载体; 变量,数学符号。 反映一种因果关系

线性方程组的表达 线性电路的数学表达模型 Ax Bf X+Ax x+Bf xx Ax-Bf =(1+A)x-Bf :-a+0- 联接矩阵:C=[(1+A)-B] 例:
2 0 1 21 22 11 12 us x x z z z z 线性方程组的表达 例: 线性电路的数学表达模型 f x x A B x x Ax Bf A x Bf x Ax x Bf Ax Bf [(1 ) ] (1 ) 联接矩阵:C= [(1 A) B]

x=[(1+A)-B] f -6-0 1+Z12 1 211+22 x2 0 u. 特点: Z11+1 Z22+1 (1)每个路径是单向的; 112 X2 (2)随时间而向前流动 1 121
- 1 u S x 1 z21 x 2 z11+1 z22+1 z12 特点 : ( 1 )每个路径是单向的; ( 2)随时间而向前流动 s s uxx z z z z u xx z z z z xx xx fx x A B 21 21 22 11 12 21 21 22 11 12 21 21 1 0 1 1 01 0 1 1 0 [(1 ) ]

二、Moson公式 ∑PnAm △ Pm第m条前向路径传输值 △m第m条前向路径不接触的子图的图行列式 △图行列式,由下式给出: △=1->∑L+>∑-∑R+.+(-1)∑LR+. Moson公式的意义:流图的规则更直观
二、Moson公式 m m m j j P f x T 1 ... (1) ... 1 2 3 i k i Lk Lk Lk L Pm 第m条前向路径传输值 m 第m条前向路径不接触的子图的图行列式 图行列式,由下式给出: Moson公式的意义:流图的规则更直观

证明:(自学) 对于线性方程
证明:(自学) 对于线性方程

例: Z31 G i Step1:写出节点不定导纳矩阵方程 G,+G2-G2 0 -G2 G2+G+sC3 -G4 u2 二 0 0 -G4 Ga+sCs 0 思考:A=?B=?
1 3 Z31 i u 0 0 0 0 1 3 2 1 4 4 5 2 2 4 3 4 1 2 2 i u u u G G s C G G G s C G G G G G1 G2 G4 C3 C5 i1 例: Step 1:写出节点不定导纳矩阵方程 思考:A=? B=?
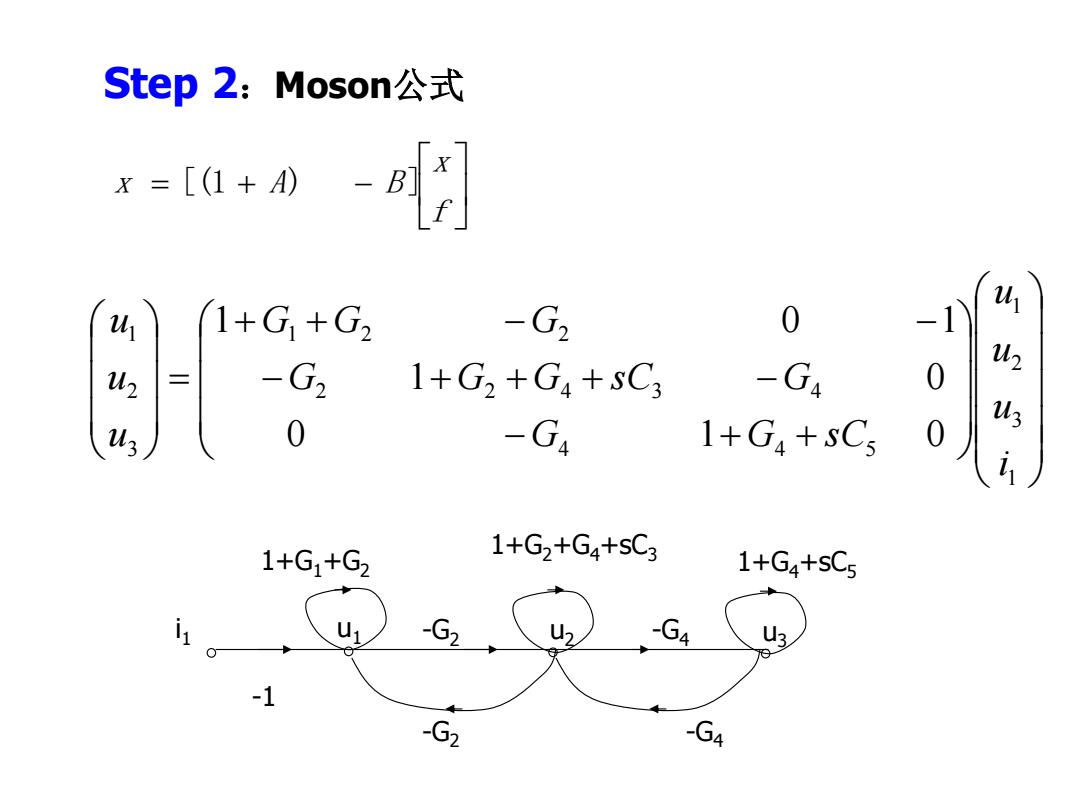
Step2:Moson公式 -a0 1+G+G2 -G2 0 -1 u 三 -G2 1+G2+G4+sC3 -G4 0 43 0 -G4 1+G4+sC5 0 1+G1+G2 1+G2+G4+sC3 1+G4+sC5 -G2 U2 03 -1 G2 GA
1 3 2 1 4 4 5 2 2 4 3 4 1 2 2 3 2 1 0 1 0 1 0 1 0 1 i u u u G G s C G G G s C G G G G u u u Step 2:Moson公式 -1 i1 u1 -G2 u2 1+G1+G2 1+G2+G4+sC3 u3 -G2 1+G4+sC5 -G4 -G4 f x x [(1 A) B ]
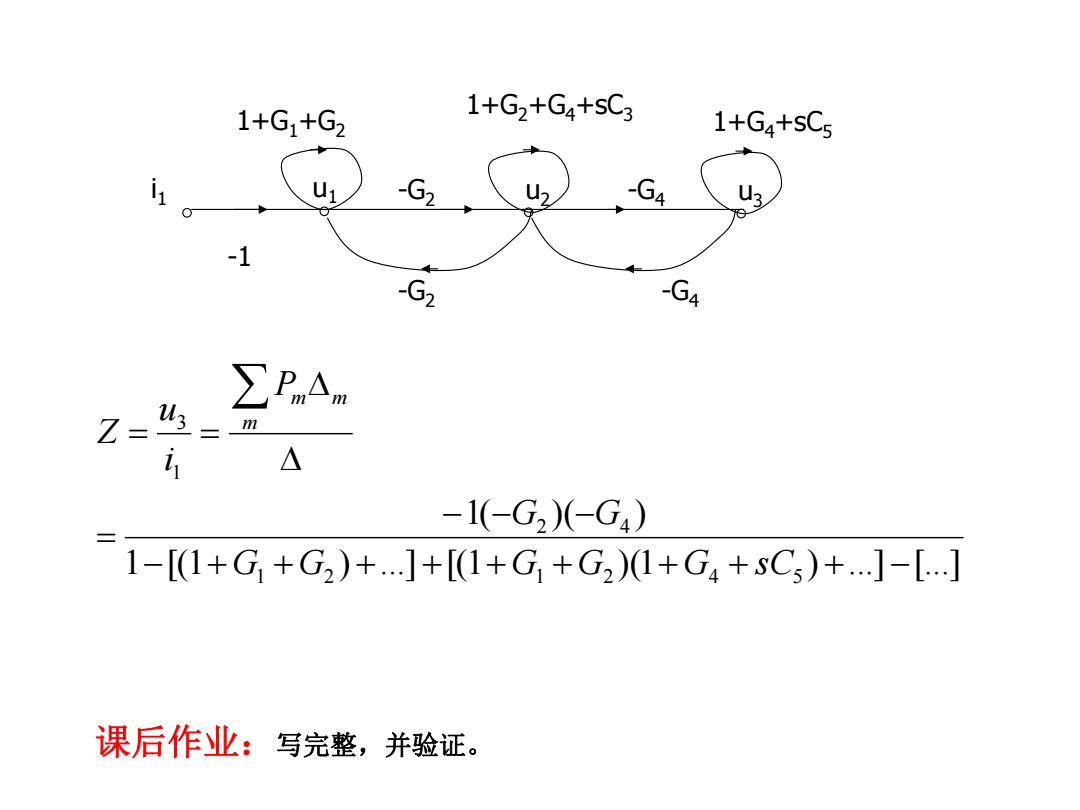
1+G1+G2 1+G2+G4+sC3 1+G4+sC5 G2 U> 4 U3 -1 G2 ∑PnAm Z m △ -1(-G2)(-G4) 1-[1+G,+G2)+.]+[(1+G+G2)1+G4+sC5)+]-[] 课后作业:写完整,并验证
1 [(1 ) ...] [(1 ) (1 ) ...] [...] 1( ) ( ) 1 2 1 2 4 5 2 4 1 3 G G G G G s C G G P i u Z m m m -1 i1 u1 -G2 u2 1+G1+G2 1+G2+G4+sC3 u3 -G2 1+G4+sC5 -G4 -G4 课后作业:写完整,并验证

同例: /1 G, G4 Z31 i 另解 (1)列写节点方程: G1+G2 -G2 0 4 -G2G2+Gx+sC -G4 u2 0 0 -G4 0
1 3 Z31 i u 0 0 0 0 1 3 2 1 4 4 5 2 2 4 3 4 1 2 2 i u u u G G s C G G G s C G G G G G1 G2 G4 C3 C5 i1 同例: (1)列写节点方程: 另解