
第5讲不定导纳函数 一第三章网络函数
第5讲 不定导纳函数 —第三章 网络函数
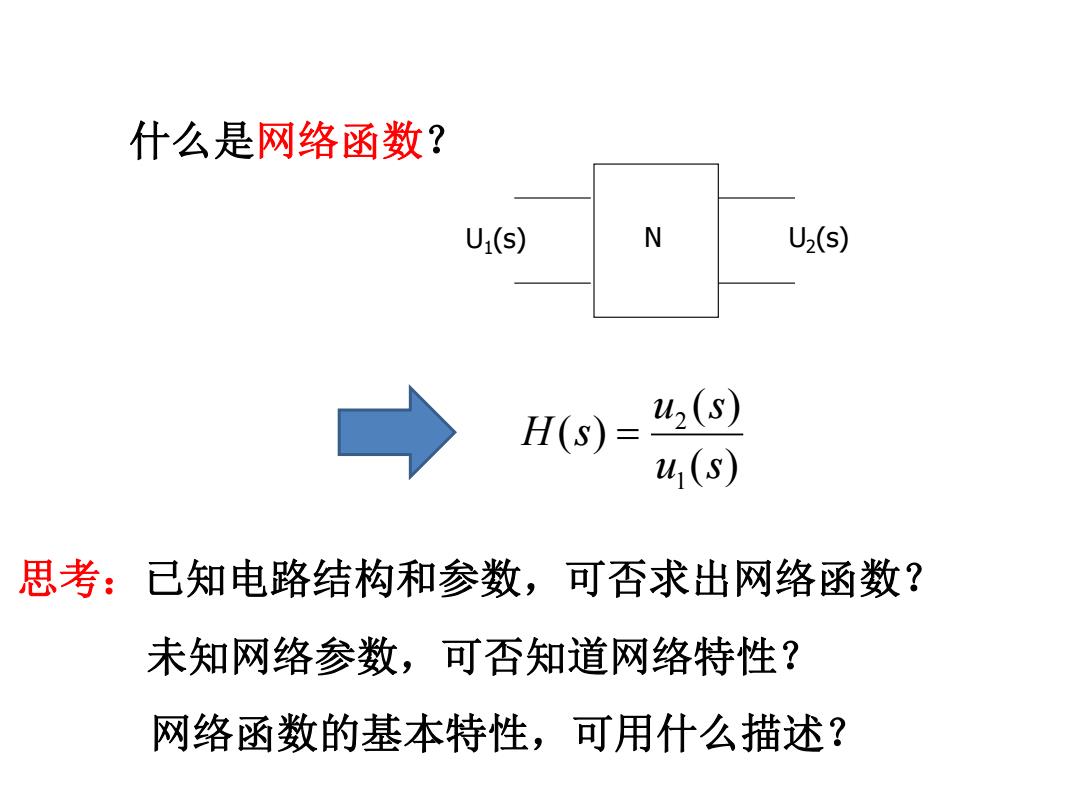
什么是网络函数? U1(s) N U2(s) Hs)= 2(S) u,(s) 思考:已知电路结构和参数,可否求出网络函数? 未知网络参数,可否知道网络特性? 网络函数的基本特性,可用什么描述?
N U2 U (s) 1 (s) ( ) ( ) ( ) 1 2 u s u s H s 什么是网络函数? 思考:已知电路结构和参数,可否求出网络函数? 未知网络参数,可否知道网络特性? 网络函数的基本特性,可用什么描述?
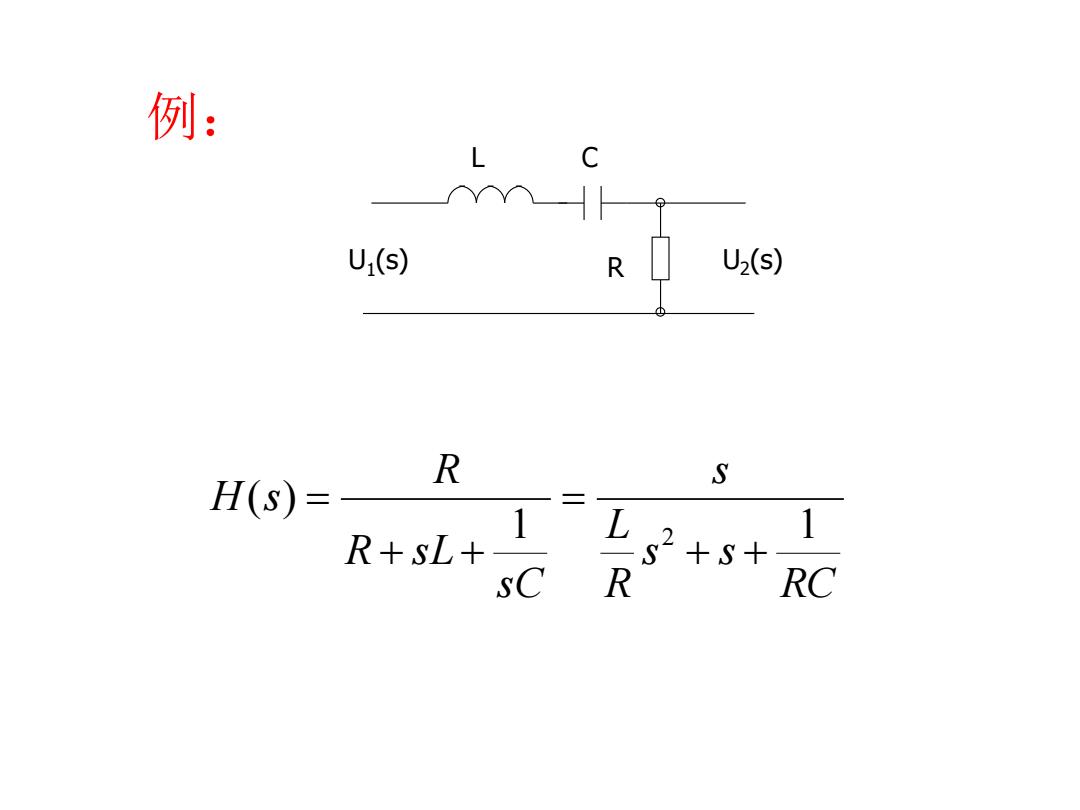
例: U1(S) R U2(S) R S H(S)= 二 1 2+s+ 1 R+SL+ sC R RC
RC s s RL s s C R s LR H s 1 1 ( ) 2 例: U 2 U (s) 1 (s) L C R
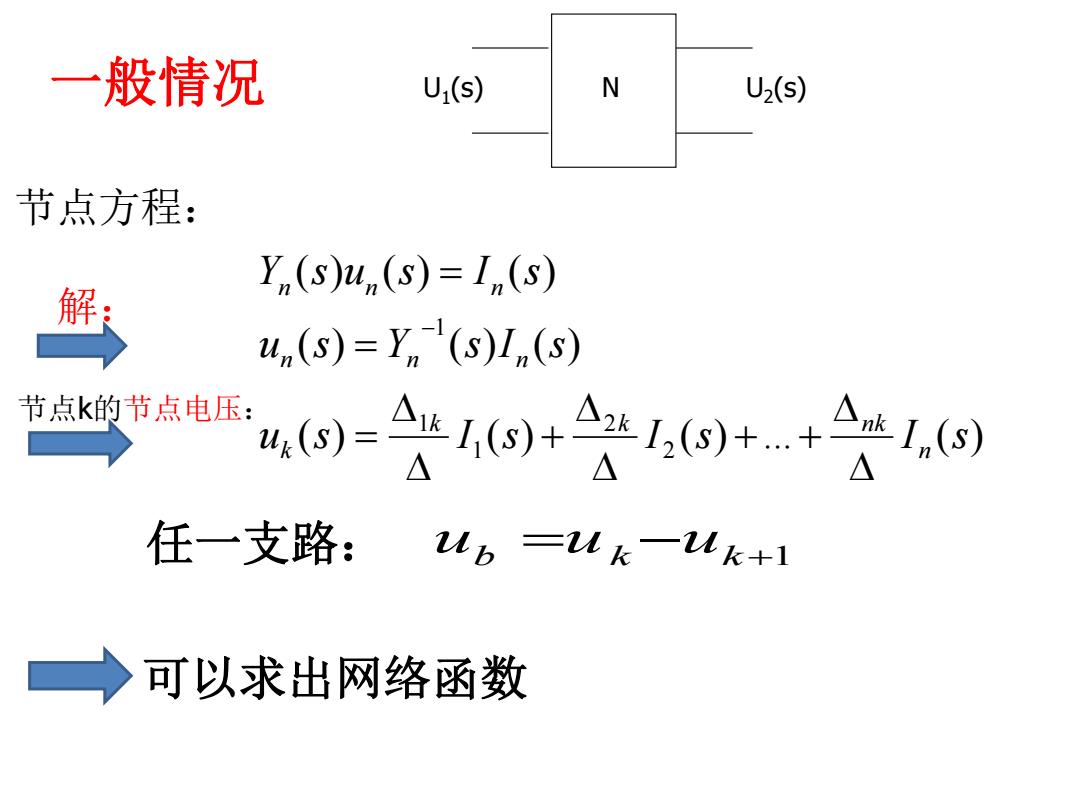
一般情况 Uj(s) N U2(S) 节点方程: Y,(s)u,(s)=1(s) 解: u,(s)=Y(s)I(s) 节点k的节点电压: 4=4o+告4,o++会, 任一支路: Lb=Lk一Mk+1 →可以求出网络函数
( ) ( ) ( ) ... ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 1 1 1 u s I s I s I s u s Y s I s Y s u s I s n k k nk k n n n n n n ub uk uk1 N U2 U (s) 1 一般情况 (s) 任一支路: 可以求出网络函数 节点方程: 解: 节点k的节点电压:

一般情况 H(S)= N(s)bmsm+bmsm+.+s+bo D(s)as"+ans"+...+as+ao 2bs i=0 ay k=0 一般:n≥m Πs-z) H(s)=Ki (s-Pk) k=1
n k k k m i i i n n n n m m m m a s b s a s a s a s a b s b s b s b D s N s H s 0 0 1 0 1 1 1 0 1 1 ... ... ( ) ( ) ( ) n k k m i i s p s z H s K 1 1 ( ) ( ) ( ) 一般情况 一般:n≥m

一、网络函数零极点 网络函数的特性,主要由零极点确定 >瞬态响应: h(t)←>H(s) Πs-) H(S)=K回 -4 ΠI6-p )S-p h(0)=∑Aew k=1 其中: A=(s-P)H(s)-k()(p) (P&-p)(Pk-p2)...(Pk-pn)
h(t) H (s) n k k k n k k m i i s p A s p s z H s K 1 1 1 ( ) ( ) ( ) n k p t k k h t A e 1 ( ) ( ) ( )...( ) ( ) ( )...( ) ( ) ( ) 1 2 1 2 k k k n k k k m k k s p p p p p p p p z p z p z A s p H s K k 网络函数的特性,主要由零极点确定 一、网络函数零极点 瞬态响应: 其中:

冲激波形,主要由极点确定; 冲激幅度,极点与零点共同确定。 >稳定特性: h()=∑Apep X k=1 X Πs-2) H(s)=K 、Ak Πs-p) 长s-2 k_1 思考:时域? 零极点分布?
n k k k n k k m i i s p A s p s z H s K 1 1 1 ( ) ( ) ( ) n k p t k k h t A e 1 ( ) 冲激波形,主要由极点确定; 冲激幅度,极点与零点共同确定。 稳定特性: 思考:时域? 零极点分布?

>稳定特性: h(t) jo 0
(t) 稳定特性: h(t) j
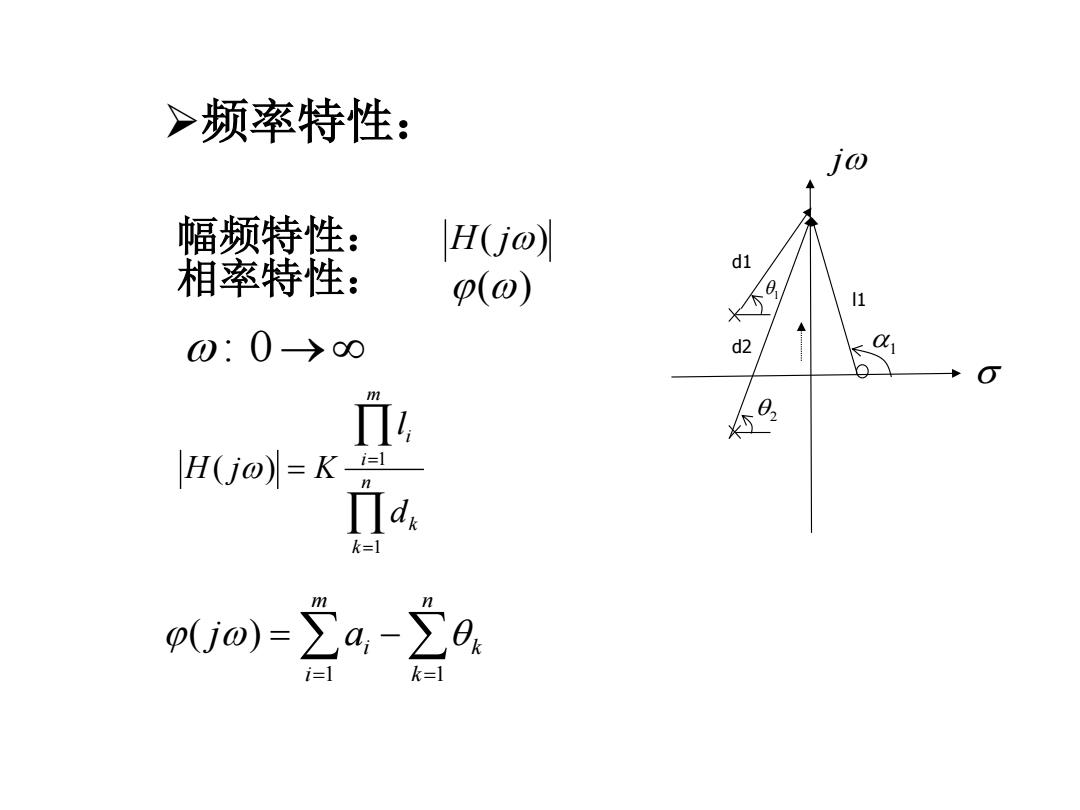
>频率特性: jo 幅频特性: H(j@) 相率特性: d1 p(0) 11 0:0→00 d2 4, H(Uo)=K Πd k= oUm)=∑4-20. :1
n k k m i i dl H j K 11 ( ) H( j ) n k k m i a i j 1 1 ( ) ( ) 频率特性: : 0 幅频特性: 相率特性: 1 2 d1 d2 l1 j 1
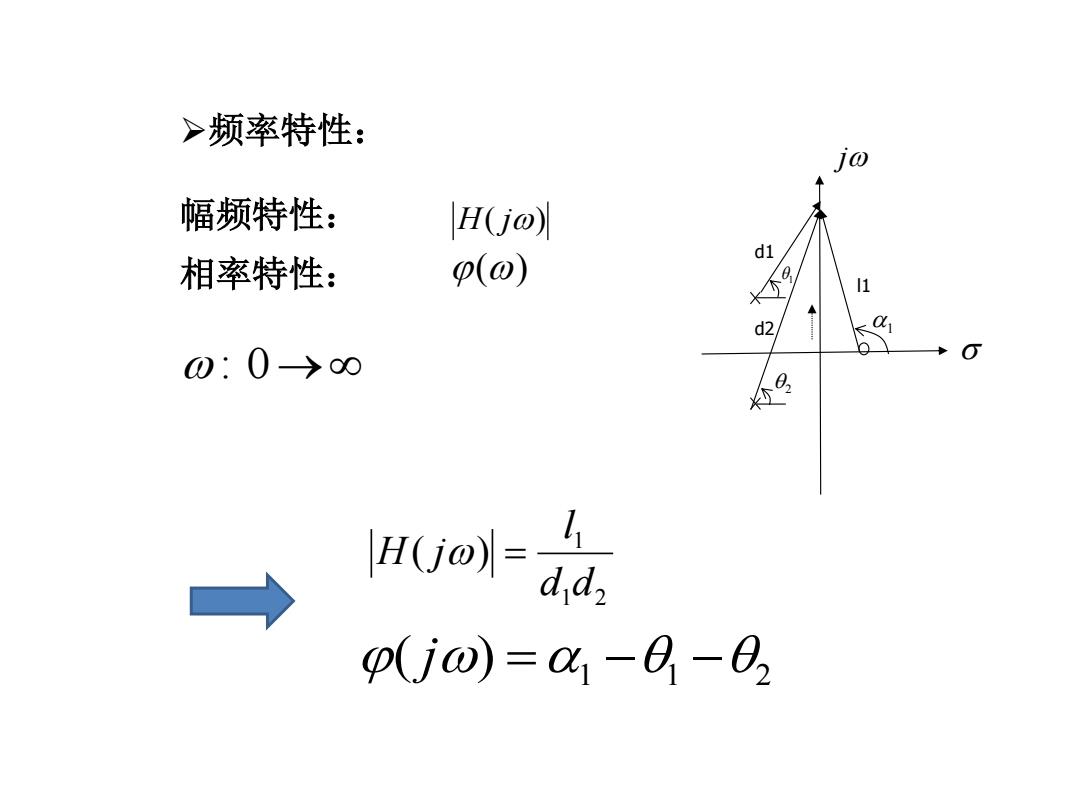
>频率特性: jo 幅频特性: H(jo) d1 相率特性: p(o) 1 d2 a 0:0>00 0 → o点 p(jo)=1-8-0
1 2 1 ( ) d dl H j H ( j ) 1 1 2 ( j ) ( ) 频率特性: : 0 幅频特性: 相率特性: 1 2 d1 d2 l1 j 1