
Chapter7 Waveletsanron Ping Zhang E-mail:pingzh@uestc.edu.cn
Ping Zhang E-mail: pingzh@uestc.edu.cn

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 参考资料 >(美)多布著,李建平译,小波十讲,国防工业出版社,2011 >孙延奎著,小波变换与图像、图形处理技术(第二版),清华大学出版社,2018 >朱希安等编著,小波分析及其在数字图像处理中的应用,电子工业出版社,2012 小波变换 小波十讲 与国像、图形处理技术 (修订版) (第2版) 补城室西 Ten Lectures on 朱希安曹林编酒 Wavelets 小波分析及其在 数字图像处理中的应用 【英Ingrid Daubechies若 Wavelet Analysis and Its Application in Digital image Processing 李建平择 4 真学3大学出量阳 图重子王学出接出
参考资料 ➢(美)多布著,李建平译,小波十讲,国防工业出版社 ,2011 ➢孙延奎著,小波变换与图像、图形处理技术(第二版),清华大学出版社,2018 ➢朱希安等编著,小波分析及其在数字图像处理中的应用,电子工业出版社,2012

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction 小波分析是纯数学、应用数学和工程技术的完美 结合。它具有良好的局部时频聚焦性,而被称为 “数学显傲镜”。 0.8 06 02 02 m=1
小波分析是纯数学、应用数学和工程技术的完美 结合。它具有良好的局部时频聚焦性,而被称为 “数学显微镜” 。 Introduction
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction ■What is the wavelets? time a time b Small wave,varying frequency and limited duration;an attempt to reveal both the frequency and temporal information in the transform domain
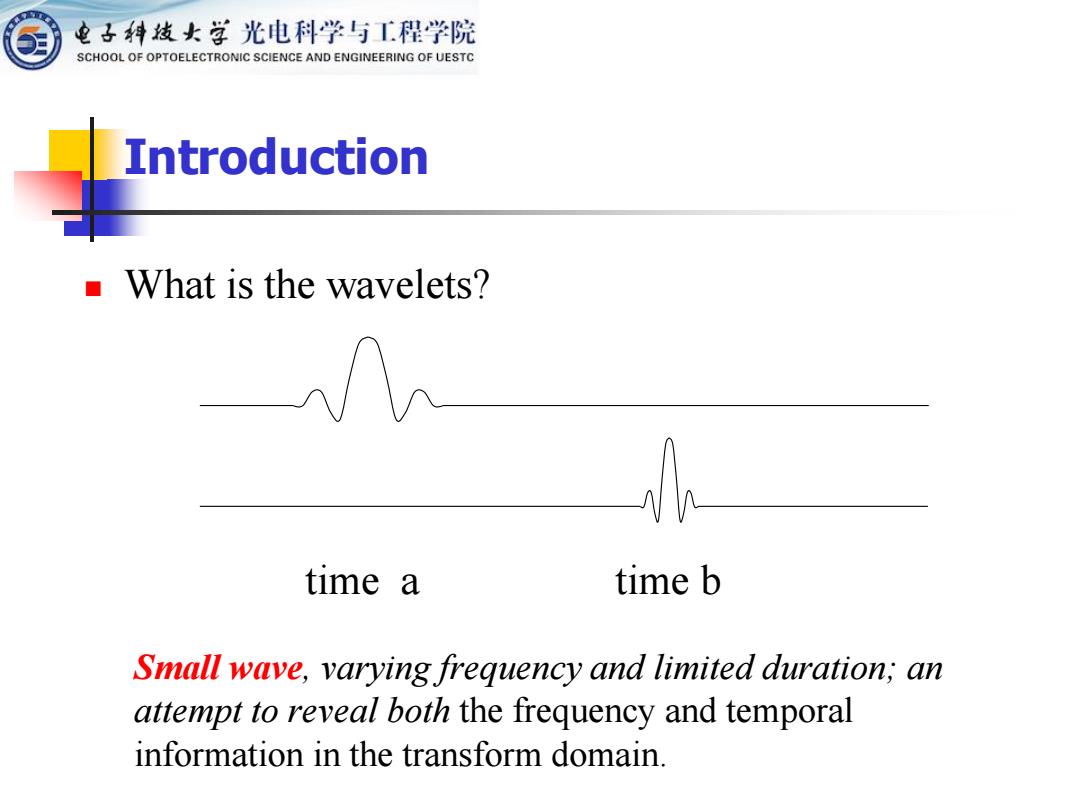
Small wave, varying frequency and limited duration; an attempt to reveal both the frequency and temporal information in the transform domain. time a time b ◼ What is the wavelets? Introduction
电子科枝女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction Satisfy two conditions (1)It must be oscillation. (2)Its amplitude is non-zero only in a very short period of interval,i.e.localization. 0.8 0.6 0.5 0.4 0.2 0 -0.5 -0.2 -8-6-4-202468 -8-6-4-202468 wavelet 1 wavelet 2
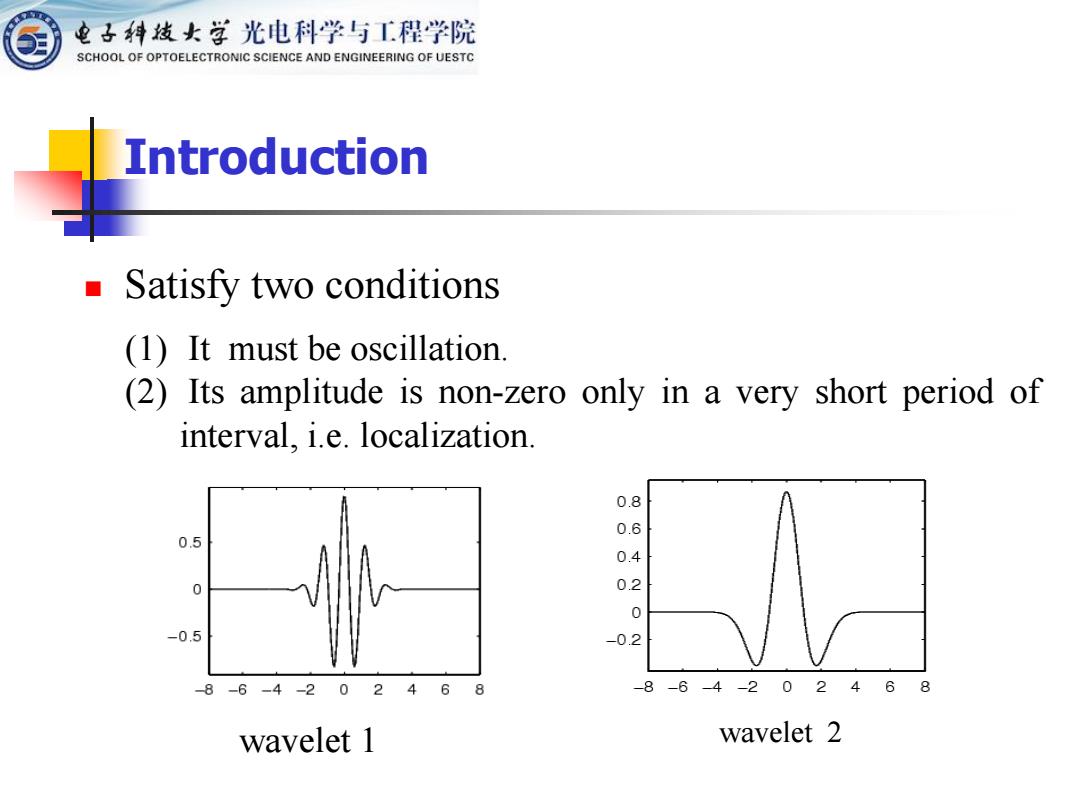
(1) It must be oscillation. (2) Its amplitude is non-zero only in a very short period of interval, i.e. localization. wavelet 1 wavelet 2 Introduction ◼ Satisfy two conditions
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction ■What is the wavelets? KUAAD Non-wavelet
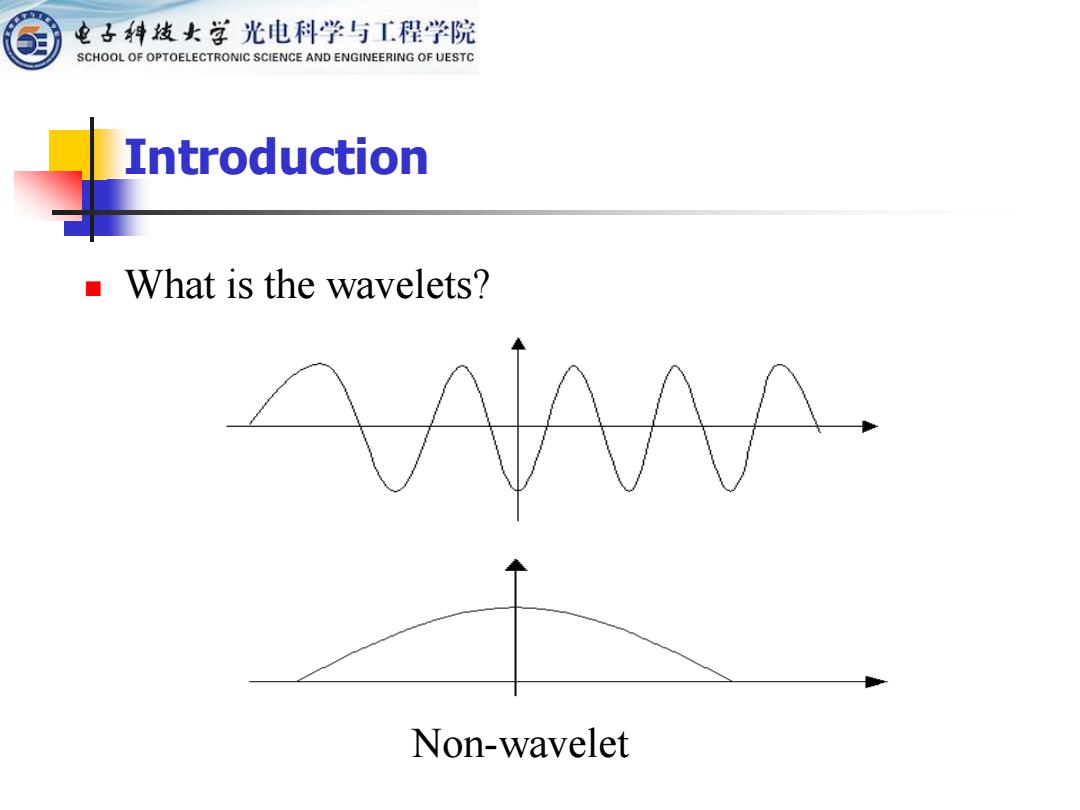
Non-wavelet Introduction ◼ What is the wavelets?
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 傅里叶变换与小波变换 v .WM→ >傅里叶变换的基础函数是正弦函数。 >小波变换基于一些小型波,称为小波,具有变化的频率和有限的持续时间
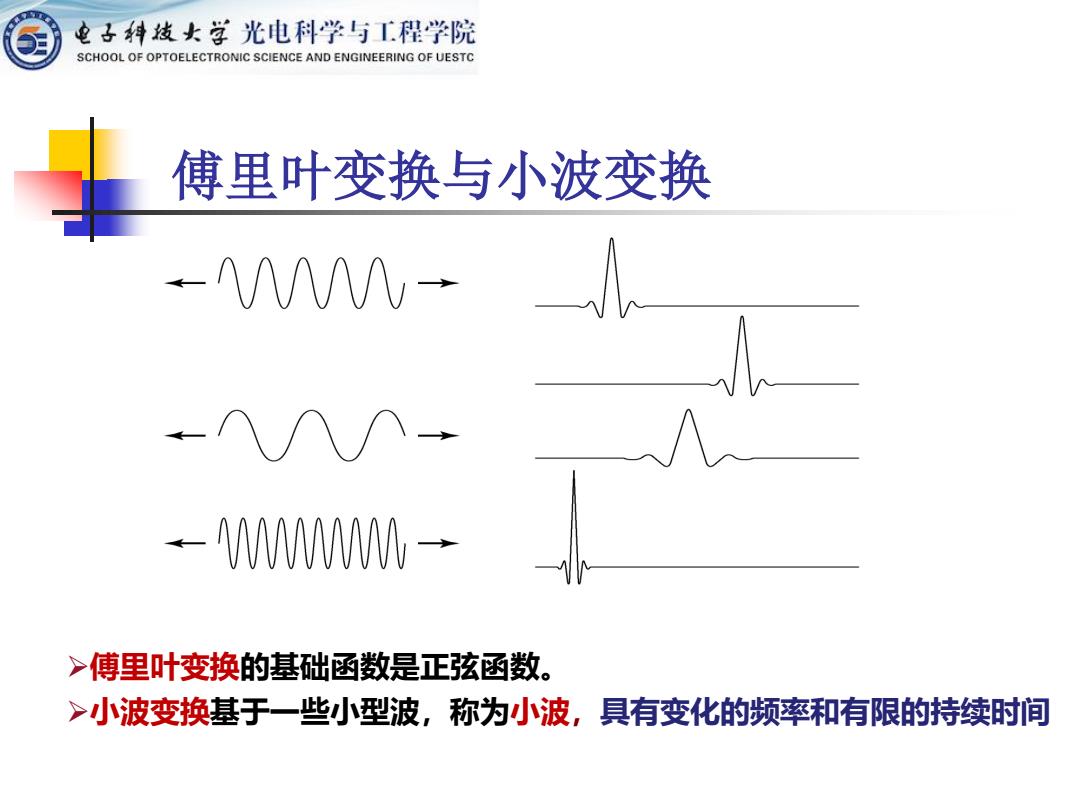
傅里叶变换与小波变换 ➢傅里叶变换的基础函数是正弦函数。 ➢小波变换基于一些小型波,称为小波,具有变化的频率和有限的持续时间

电子残发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction The wavelet transform Λ∧ΛΛΛΛ∧Λ∧Λ Fourier basis W Wavelet basis Sampling basis Local time-frequency characteristics
Local time-frequency characteristics Sampling basis Wavelet basis Fourier basis Introduction ◼ The wavelet transform

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 傅里叶变换与小波变换 ◆傅里叶变换反映的是图像的整体特征,其频域分析 具有很好的局部性,但空间(时间)域上没有局部化 功能。 ◆小波变换是空间(时间)和频率的局部变换,通过伸 缩平移运算对信号逐步进行多尺度细化,能自动适 应时频信号分析的要求,从而可聚焦到信号的任意 细节
傅里叶变换与小波变换 ◆ 傅里叶变换反映的是图像的整体特征,其频域分析 具有很好的局部性,但空间(时间)域上没有局部化 功能。 ◆ 小波变换是空间(时间)和频率的局部变换,通过伸 缩平移运算对信号逐步进行多尺度细化,能自动适 应时频信号分析的要求,从而可聚焦到信号的任意 细节

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Introduction ◆小波变换(Wavelets Transform,WT)」 具有良好的局部时频聚焦特性, 而被称为"数学显微镜”(Mathematical microscope)。 ◆小波分析(Wavelets Analysis,.WA)是纯数学、应用数学和工程技术的 完美结合。从数学方面来说,它是大半个世纪“调和分析”的结晶 (include Fourier analysis,function space,etc. ◆WT是20世纪最辉煌的科学成就之一。它在信号处理、图像处理、模 式识别、机器视觉、语音识别、地震勘探、量子物理、流体力学、电磁 场、CT成象、故障诊断、分形、数值计算等具有极其广泛的应用
◆ 小波变换(Wavelets Transform,WT)具有良好的局部时频聚焦特性, 而被称为“数学显微镜”(Mathematical microscope)。 ◆ 小波分析(Wavelets Analysis,WA)是纯数学、应用数学和工程技术的 完美结合。从数学方面来说,它是大半个世纪“调和分析”的结晶 (include Fourier analysis, function space, etc.)。 ◆ WT是20世纪最辉煌的科学成就之一。它在信号处理、图像处理、模 式识别、机器视觉、语音识别、地震勘探、量子物理、流体力学、电磁 场、CT成象、故障诊断、分形、数值计算等具有极其广泛的应用。 Introduction