
电子科发女学 Unversityf Electranie Scesce TechelogChina 信号处理理论 与算法 第六章 滤波器组基础
第六章 滤波器组基础 信号处理理论 与算法
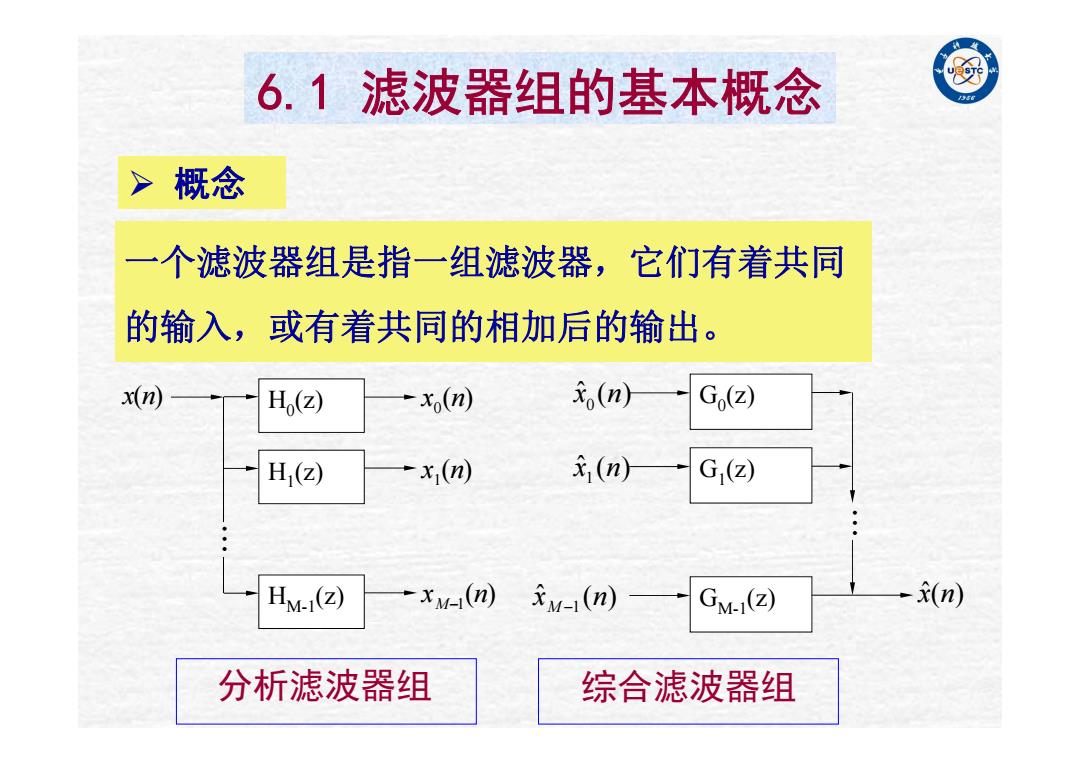
6.1滤波器组的基本概念 >概念 一个滤波器组是指一组滤波器,它们有着共同 的输入,或有着共同的相加后的输出。 x(n H (z) x(n) (n) Go(Z) H,(Z) x,(n) (n) G(Z) HM-1(Z) -xM-(m)元M-(n)) GM-1(Z) (n) 分析滤波器组 综合滤波器组
6.1 滤波器组的基本概念 概念 一个滤波器组是指一组滤波器,它们有着共同 的输入,或有着共同的相加后的输出。 分析滤波器组 综合滤波器组 H 0(z) ( ) x 0 n H1(z) ( ) x1 n HM-1(z) ( ) x M 1 n x ( n ) G 0 ˆ ( ) (z) x 0 n G1 ˆ ( ) (z) x1 n GM-1 ˆ ( ) (z) x M 1 n xˆ ( n )

>分析滤波器组H(z),H,(z),..H-(z)的作用 将信号按频带分解,分解为低通、一系列带通和 高通信号。按信号能量的分布,或按重要性,给以分 别的处理。去除抽取时的混叠。 H(e) H(e) Ha(e) 无混叠 2 2k+0 2n Ho(e) H(e) H(e) 有混叠 2π
分析滤波器组 , ,… 的作用 将信号按频带分解,分解为低通、一系列带通和 高通信号。按信号能量的分布,或按重要性,给以分 别的处理。去除抽取时的混叠。 H 0(z) H 1(z) ( ) H M 1 z 0 ( ) 0 j H e ( ) j k H e ( ) 1 j k H e k M 2 ( 1) 2 k M 2 0 ( ) 0 j H e ( ) j k H e ( ) 1 j k H e k M 2 ( 1) 2 k M 2 无混叠 有混叠
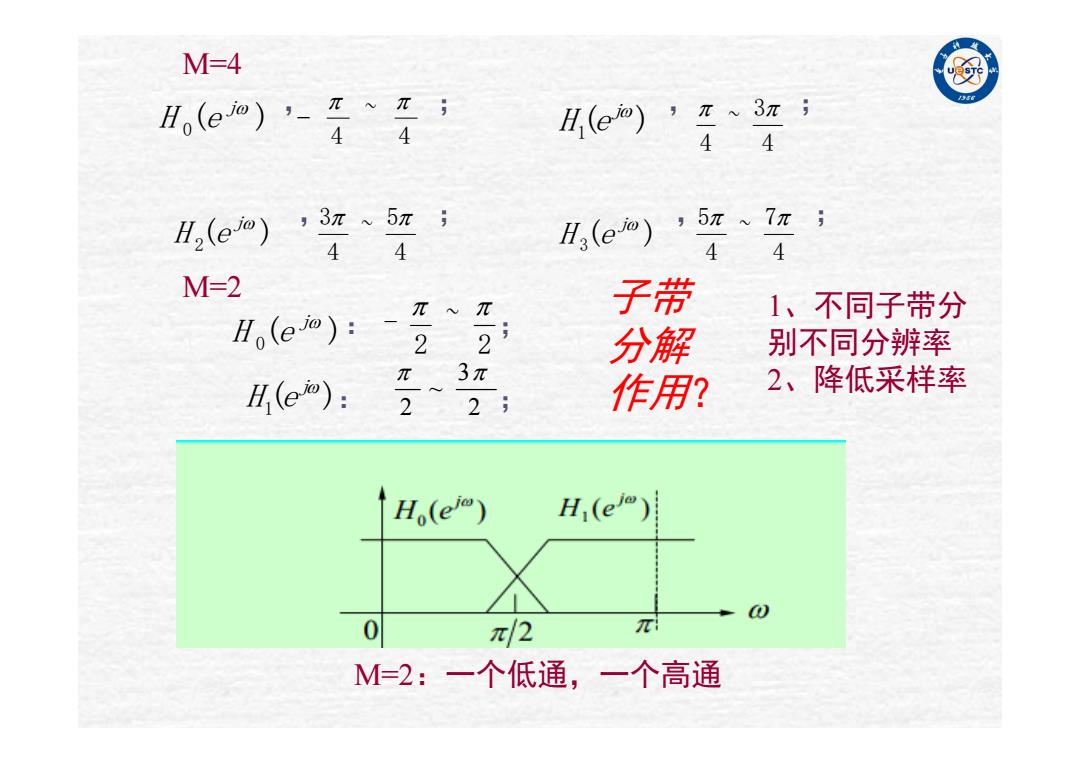
M=4 例 H(eo)’- 4 4 H(eo)’刀~3πi 44 H,(eio) ,3π5π; H(eo) ,5π心7π; 4 4 4 4 M=2 π~π 子带 1、不同子带分 分解 别不同分辨率 3π H(e): 29 作用? 2、降低采样率 Ho(ej) H(e) 0 π/2 π M=2:一个低通,一个高通
4 ~ 4 4 3 ~ 4 4 5 ~ 4 3 4 7 ~ 4 5 0( ) j H e M=4 , ; ,; ,; ,; 1( ) j H e ( ) 2 j H e ( ) 3 j H e M=2 : ; : ; 0( ) j H e 2 ~ 2 - 1( ) j H e 3 ~ 2 2 M=2:一个低通,一个高通 子带 分解 作用? 1、不同子带分 别不同分辨率 2、降低采样率
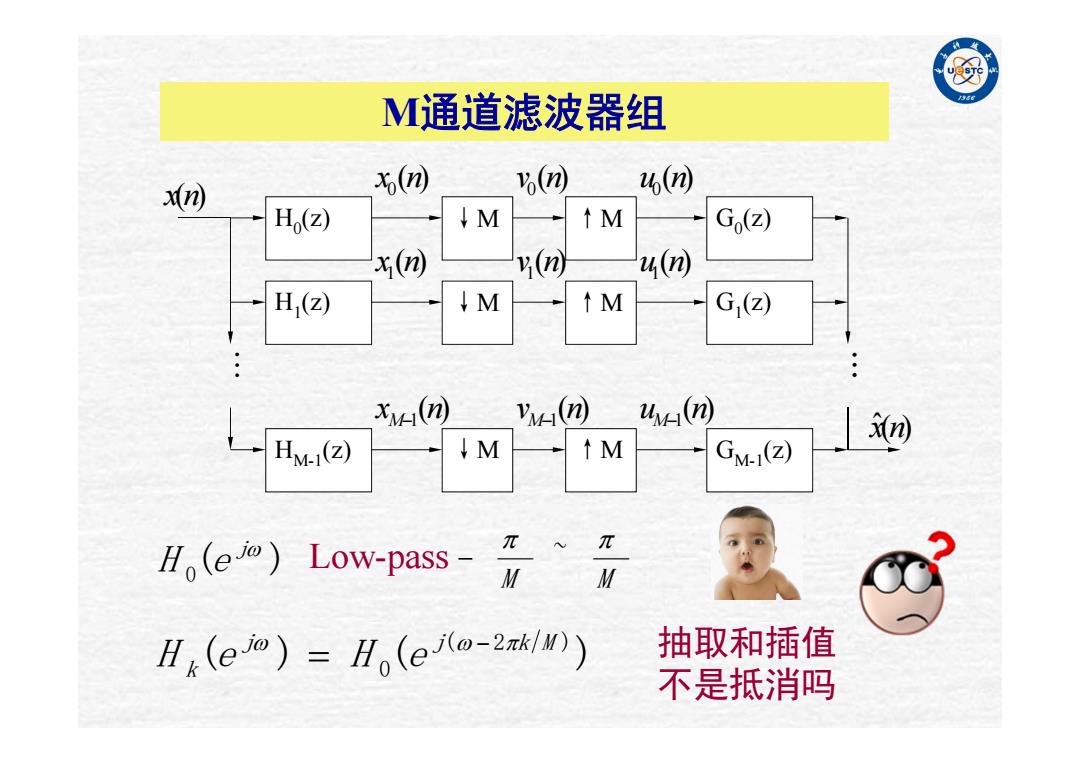
例 M通道滤波器组 m x回 ) 6(m H,(Z) ↓M ↑M G() xn 4) H(Z) ↓M ↑M G,() xn) n uv(n n HM-i(Z) ↓M ↑M GM.1(Z) (e)Low-pass- π~π M H4(e)=H(eo-2w) 抽取和插值 不是抵消吗
M通道滤波器组 M M ( ) ~ 0 j H e Low-pass ( ) ( ) ( 2 ) 0 j j k M H k e H e x(n) ( ) 1x n ( ) 1v n ( ) 1 u n H0(z) ↓M ↑M G0(z) H1(z) ↓M ↑M G1(z) HM-1(z) ↓M ↑M GM-1(z) ( ) 0x n ( ) 1 x n M ( ) 0v n ( ) 1 v n M ( ) 0 u n ( ) 1 u n M x ˆ(n) 抽取和插值 不是抵消吗

>综合滤波器组G,(z),..G-1(z的作用 去除插值后的镜像,实现真正的插值, 重建原信号 M:由于每一个子带信号的频率降为原来的1/M,所 以抽样频率可降低M倍; M:恢复原来的抽样频率,使重建的信号和原信号有 相同的抽样频率。 既抽取又插值的作用: >达到按信号能量分布给以不同处理的目的,如编码; > ,抽取后的信号可能要传输很远才重建
综合滤波器组 ,… 的作用 去除插值后的镜像,实现真正的插值,重建原信号 M:由于每一个子带信号的频率降为原来的1/M,所 以抽样频率可降低M倍; M:恢复原来的抽样频率,使重建的信号和原信号有 相同的抽样频率。 既抽取又插值的作用: 达到按信号能量分布给以不同处理的目的,如编码; 抽取后的信号可能要传输很远才重建。 ( ) G 0 z G M 1(z)
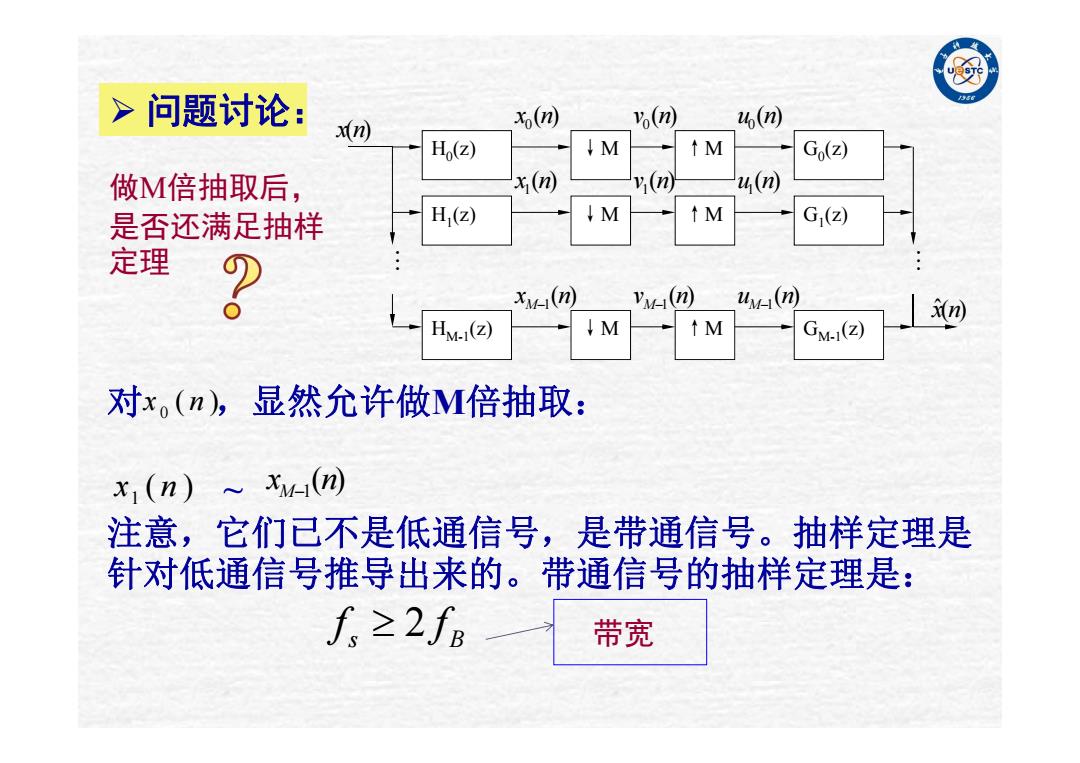
>问题讨论: m x() (m) 4( H (z) ↓M ↑M Go(z) 做M倍抽取后, x(n v (n 4(m 是否还满足抽样 H(Z) ↓M ↑M G(Z) 定理 xv(n) VMa(O uv (n) Hy-i(Z) ↓M ↑M GM-i(Z) 对x。(n),显然允许做M倍抽取: x1(n)≈xw-(n 注意,它们已不是低通信号,是带通信号。抽样定理是 针对低通信号推导出来的。带通信号的抽样定理是: f,≥2∫B 带宽
问题讨论: 对 ,显然允许做M倍抽取: ~ 注意,它们已不是低通信号,是带通信号。抽样定理是 针对低通信号推导出来的。带通信号的抽样定理是: 做M倍抽取后, 是否还满足抽样 定理 1 x n( ) 1( ) Mx n 2 s B f f 带宽 x(n) ( ) x1 n ( ) v1 n ( ) u1 n H0(z) ↓M ↑M G0(z) H1(z) ↓M ↑M G1(z) HM-1(z) ↓M ↑M GM-1(z) ( ) x0 n ( ) xM1 n ( ) v0 n ( ) vM1 n ( ) u0 n ( ) uM1 n x ˆ(n) 0 x ( ) n

例 希望:x(n)=x(n) Perfect Reconstruction(PR) 如果:x(m)=cx(n-n),C,乃都是常数 Perfect Reconstruction(PR) 否则:即产生x(n)对x(n)的失真。 需研究失真的原因!
希望: = Perfect Reconstruction(PR) 如果: ,, 都是常数 Perfect Reconstruction(PR) 否则:即产生 对 的失真。 需研究失真的原因! x n( ) x n( ) 0 x n cx n n () ( ) c n0 x n( ) x n( )

呀 x(n)对x(n)失真的因素: 1.混叠失真:抽样频率不满足 ∫,≥2M 2.幅度及相位失真:滤波器组频带在通带内不 “平”,而其相频特性不具有线性相位所致 3.编码,量化,传输所产生的误差 (1)2M个滤波器是否要一一设计? (2)每一路的滤波是否要逐一计算? (3)如何保证PR?
(1)2M个滤波器是否要一一设计? (2)每一路的滤波是否要逐一计算? (3)如何保证PR? x(n) 对 失真的因素: x(n) 1. 混叠失真:抽样频率不满足 2 .幅度及相位失真:滤波器组频带在通带内不 “平”,而其相频特性不具有线性相位所致 3. 编码,量化,传输所产生的误差 2 s C f Mf

6.2滤波器组的种类及有关的滤波器基础 > 6.2.1最大均匀抽取滤波器组 > 6.2.2正交镜像滤波器组 >6.2.3第M带滤波器 >6.2.4半带滤波器 > 6.2.5互补型滤波器
6.2 滤波器组的种类及有关的滤波器基础 6.2.1 最大均匀抽取滤波器组 6.2.2 正交镜像滤波器组 6.2.3 第 M带滤波器 6.2.4 半带滤波器 6.2.5 互补型滤波器