
信号处理理论与算法 时频分析-信号分析基础 张朋 自动化工程学院 1
信号处理理论与算法 时频分析-信号分析基础 张 朋 自动化工程学院 1
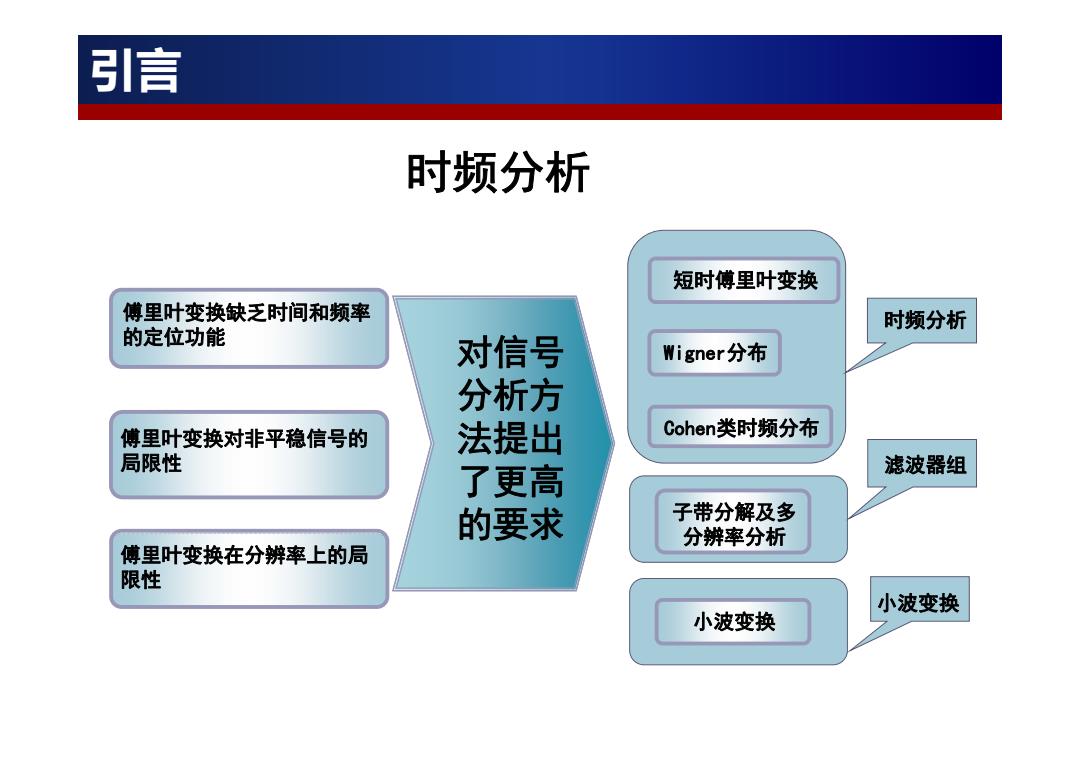
引言 时频分析 短时傅里叶变换 傅里叶变换缺乏时间和频率 时频分析 的定位功能 对信号 Wi gner分布 分析方 傅里叶变换对非平稳信号的 法提出 Cohen类时频分布 局限性 了更高 滤波器组 的要求 子带分解及多 分辨率分析 傅里叶变换在分辨率上的局 限性 小波变换 小波变换
傅里叶变换缺乏时间和频率 的定位功能 傅里叶变换对非平稳信号的 局限性 傅里叶变换在分辨率上的局 限性 对信号 分析方 法提出 了更高 的要求 短时傅里叶变换 Wigner分布 Cohen类时频分布 小波变换 子带分解及多 分辨率分析 时频分析 滤波器组 小波变换 时频分析 引言

信号的时-频联合分析 傅里叶变换 Kj2)=∫mx(0)et x0=元X(U2ed 傅里叶变换联系了时间和频率。但是,傅里叶变换存在三 方面不足。 傅里叶变换在时间、频率“定位”的不足 如要求在某一频率点处的值 X(U2)=∫xt)emdl 需要从-00~+0 如要求在某时刻处的值 需要2=-0~+0 x)=2元X(U2ed2
( ) () j t X j x t e dt 1 () ( ) 2 j t x t Xj e d 傅里叶变换联系了时间和频率。但是,傅里叶变换存在三 方面不足。 傅里叶变换 信号的时-频联合分析 傅里叶变换在时间、频率“定位”的不足 0 0 ( ) () j t X j x t e dt 0 0 1 () ( ) 2 j t x t X j e d 如要求在某一频率点处的值 需要t从 - ~+ 如要求在某时刻处的值 需要 =- ~+

信号的时-频联合分析 傅里叶变换在时间、频率“定位”的不足 设信号x()由三个不同频率的正弦所组成,即 sin(o,m),0≤n≤N1-1 x(nm={sin(o,n),N,≤n≤N2-1 sin(o,n),N2≤n≤N-1 N>N2>N,03>02>, 对x()做傅里叶变换,频谱x(e)是什么样? Linear scale Signal in time 0 ISTFT2,Lh-48.Nf-192,lin.scale,contour,Thld-5% 0.4 0.3 04 02 0.2 01 Freosoncy 0.1 0 159517975 0 50 100 150200250300 350 Time [s]
设信号x(n)由三个不同频率的正弦所组成,即 1 2 3 sin( ), ( ) sin( ), sin( ), n x n n n 1 1 2 2 0 1 1 1 n N N nN N nN 2 13 2 1 NN N , 对x(n)做傅里叶变换,频谱 是什么样? X e j 傅里叶变换在时间、频率“定位”的不足 信号的时-频联合分析
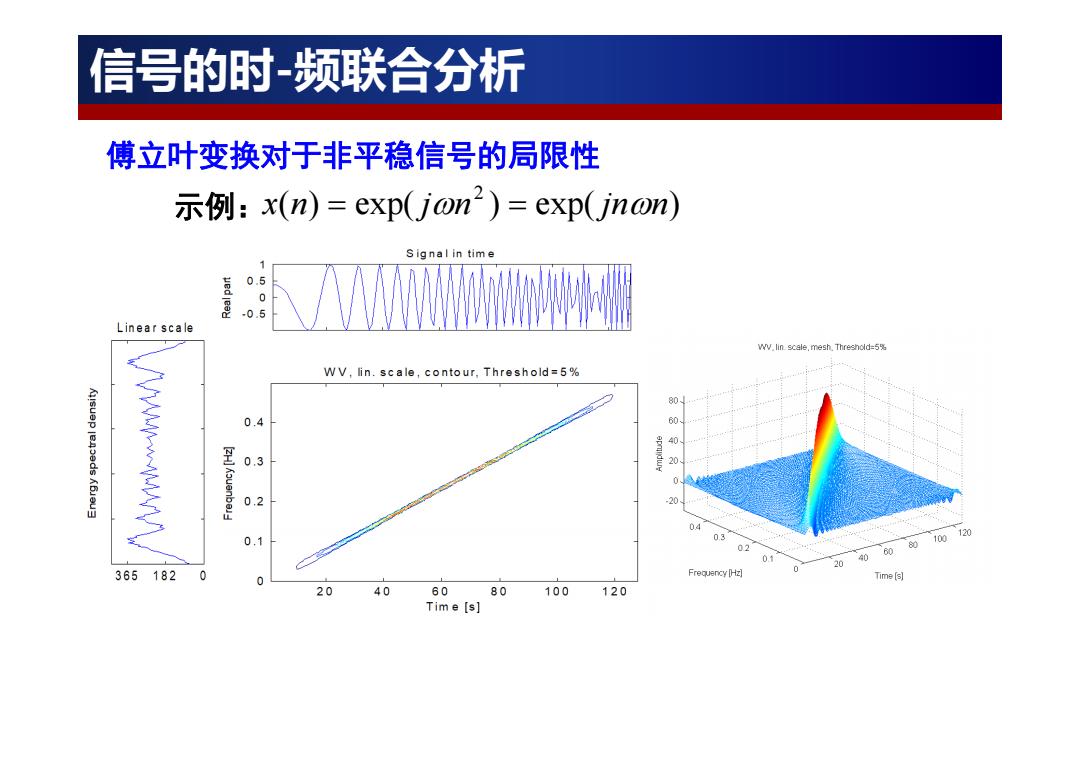
信号的时-频联合分析 傅立叶变换对于非平稳信号的局限性 示例:x(n)=exp(jon2)=exp(jnon) Signal in time 0 0 Linear scale WV.lin scale,mesh.Threshold=5% WV,lin.scale,contour,Threshold=5% 0.4 60 40 0.3 0 0.2 -20 04 120 0.1 03 02 80100 01 20 9060 365 182 0 Frequency [Hz] Time [s] 20 40 60 80 100 120 Time [s]
傅立叶变换对于非平稳信号的局限性 信号的时-频联合分析 示例: ( ) exp( ) exp( ) 2 x n j n jn n

信号的时频联合分析 傅立叶变换在分辨率上的局限性 “分辨率”包含了信号的时域和频域两个方面,它是指对信 号所能作出辨别的时域或频域的最小间隔(又称最小分辨细 胞)。 分辨能力的好坏取决于三点: 信号的特点 信号的长度 所用的算法 一个好的信号分析算法,应该能适应信号的特点自动调节时 域的分辨率和频域的分辨率
“分辨率”包含了信号的时域和频域两个方面,它是指对信 号所能作出辨别的时域或频域的最小间隔(又称最小分辨细 胞)。 分辨能力的好坏取决于三点: 信号的特点 信号的长度 所用的算法 一个好的信号分析算法,应该能适应信号的特点自动调节时 域的分辨率和频域的分辨率。 傅立叶变换在分辨率上的局限性 信号的时-频联合分析

信号的时-频联合分 傅立叶变换在分辨率上的局限性 傅立叶变换可以写成如下的内积形式:X(2)==x(t)y(t)d 若x,y均是离散的,则=∑x(n)y(n) 则信号x(t)的傅立叶变换X(2)等于x(t)在基函数e2上的正交 投影。基函数e2在频域是位于2处的δ函数。 =eig-dt=278(Q-) 用傅立叶变换来分析信号的频域行为时,它具有最好的频 率分辨率,在时域有着最坏的分辨率。对傅立叶反变换, 分辨率的情况正好相反
傅立叶变换可以写成如下的内积形式: 若x,y都是连续的,则 若x,y均是离散的,则 ( ) ( ), j t X j xt e x, y x ( t ) y ( t )dt * n x, y x ( n ) y ( n ) * 傅立叶变换在分辨率上的局限性 信号的时-频联合分析 则信号 的傅立叶变换 等于 在基函数 上的正交 投影。基函数 在频域是位于 处的 函数。 用傅立叶变换来分析信号的频域行为时,它具有最好的频 率分辨率,在时域有着最坏的分辨率。对傅立叶反变换, 分辨率的情况正好相反。 x ( t ) X ( j ) j t e x ( t ) j t e 1 2 12 ( ) 1 2 , 2( ) jt jt j t e e e dt
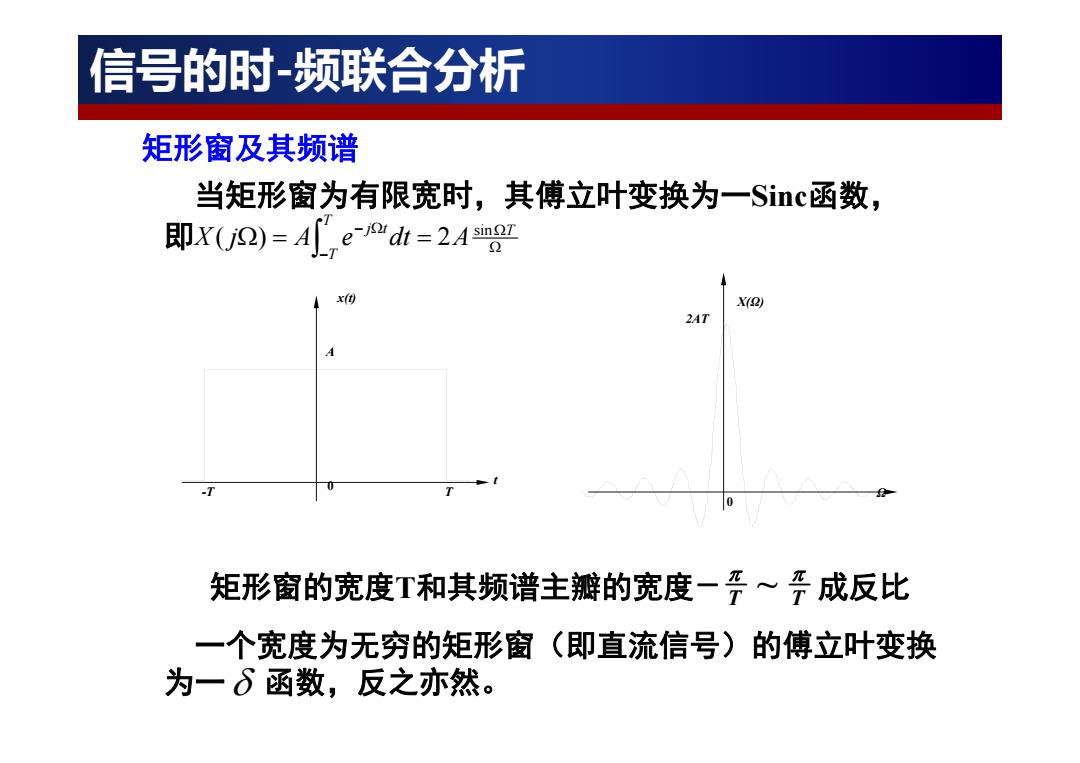
信号的时-频联合分析 矩形窗及其频谱 当矩形窗为有限宽时,其傅立叶变换为一Simc函数, 即X(U2)=[edi=2Ag x( 2AT 矩形窗的宽度T和其频谱主瓣的宽度一妥~牙成反比 一个宽度为无穷的矩形窗(即直流信号)的傅立叶变换 为一8函数,反之亦然
一个宽度为无穷的矩形窗(即直流信号)的傅立叶变换 为一 函数,反之亦然。 当矩形窗为有限宽时,其傅立叶变换为一Sinc函数, 即 -T T 0 A t x(t) Ω X(Ω) 0 2AT T T j t T X j A e dt A sin ( ) 2 矩形窗的宽度 T和其频谱主瓣的宽度 成反比 ~ T T 矩形窗及其频谱 信号的时-频联合分析

信号的时频联合分析 短时傅立叶变换(STFT) 用基函数g,n(t)=g(t-t)e2r来代替傅立叶变换中的基函数e2i = =x(r)g"(t-7)edr =STFT,(t,Q) 该式称为x(t)的短时傅立叶变换,式中8()是一窗,又称加 窗傅立叶变换。 用g(x)沿着t轴滑动,因此可以不断地截取一段一段的信号 ,然后对每一小段分别作傅立叶变换,得到(t,2)平面上的二 维函数STFT(t,2)
用基函数 j t g ( ) g(t )e , 来代替傅立叶变换中的基函数 该式称为 的短时傅立叶变换,式中 是一窗,又称加 窗傅立叶变换。 x(t) j t e j t x( ), g ( ) x( ), g(t )e , ( ) ( ) ( , ) * x g t e d STFT t x j g( ) 短时傅立叶变换(STFT) 信号的时-频联合分析 用 沿着 t 轴滑动,因此可以不断地截取一段一段的信号 ,然后对每一小段分别作傅立叶变换,得到 平面上的二 维函数 STFT (t,) x g( ) (t,)

信号的时频联合分析 STFT时域和频域分辨率由什么决定? STFT,(t,)=x(r)g'(t-t)e dr g(t)的作用是保持在时域为有限长(也称“有限支撑”), 其宽度越小,则时域分辨率越好。在频域,由于eQr为 一个δ函数,因此仍可保持较好的频域分辨率。 STFT非严格时频分布 短时傅立叶变换是最简单、最直观的时频联合分析,但变 量,2仍是单独取值,因此,它并不是严格意义上的时频联 合分析
的作用是保持在时域为有限长(也称“有限支撑”), 其宽度越小,则时域分辨率越好。在频域,由于 为 一个 函数,因此仍可保持较好的频域分辨率。 g ( ) j t e * (, ) () ( ) j x STFT t x g t ed STFT 时域和频域分辨率由什么决定? 信号的时-频联合分析 短时傅立叶变换是最简单、最直观的时频联合分析,但变 量 仍是单独取值,因此,它并不是严格意义上的时频联 合分析。 t, STFT 非严格时频分布