
离散傅里叶变换及快速算法 刘科 自动化工程学院
离散傅里叶变换及快速算法 刘科 自动化工程学院
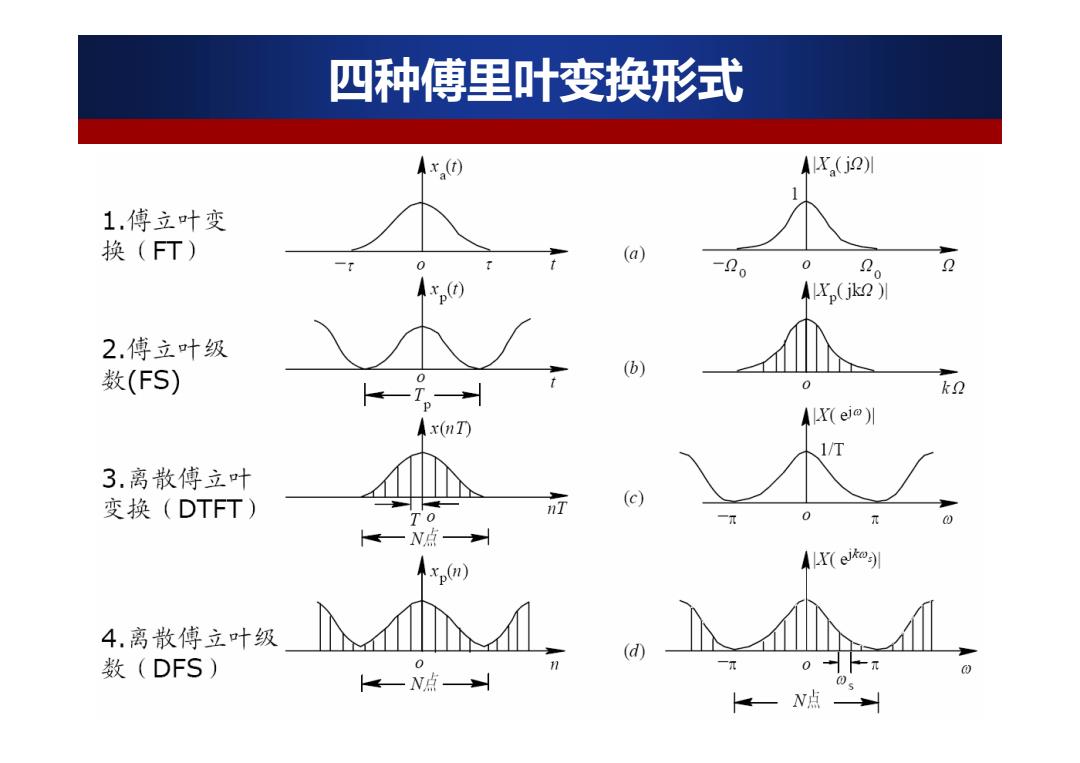
四种傅里叶变换形式 Ax() (j) 1.傅立叶变 换(FT) (a) 0 2o 2 (jk) 2.傅立叶级 数(FS) (b) kQ X(ei) Ax(nT) 3.离散傅立叶 变换(DTFT) nT (c) N点 AX(ek Axp(n) 4.离散傅立叶级 (d) 数(DFS) 一元 一N点 一N点
2 四种傅里叶变换形式
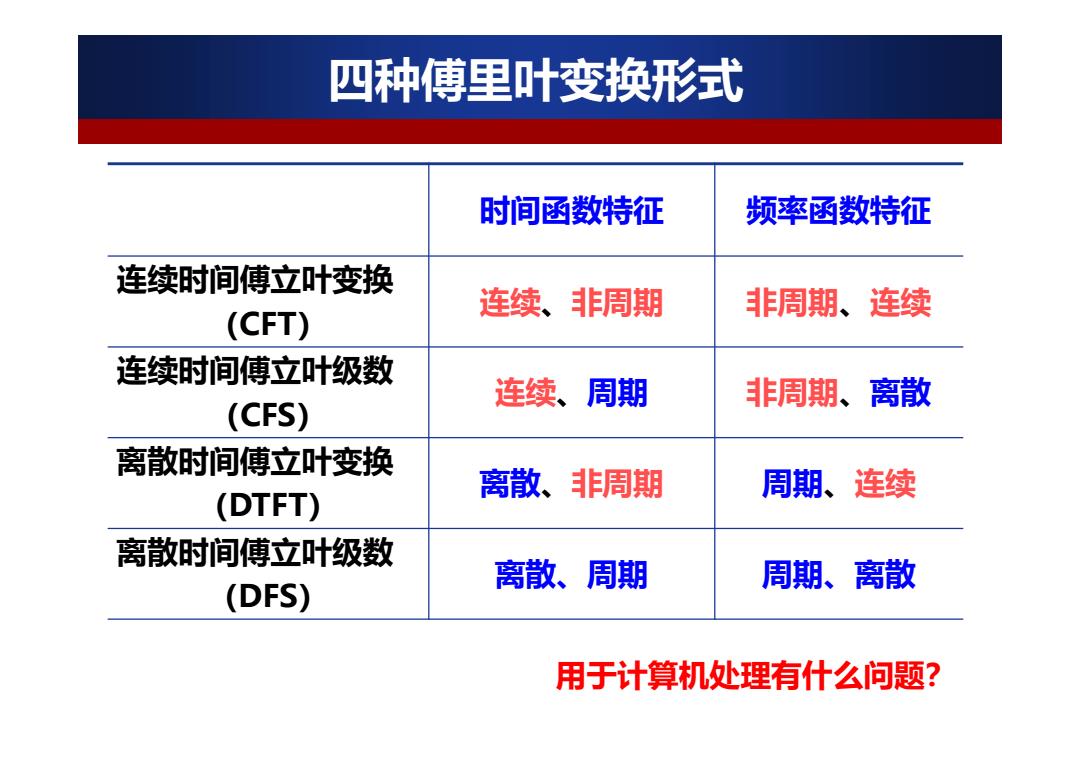
四种傅里叶变换形式 时间函数特征 频率函数特征 连续时间傅立叶变换 连续、非周期 非周期、连续 (CFT) 连续时间傅立叶级数 连续、周期 非周期、离散 (CFS) 离散时间傅立叶变换 离散、非周期 周期、连续 (DTFT) 离散时间傅立叶级数 离散、周期 周期、离散 (DFS) 用于计算机处理有什么问题?
四种傅里叶变换形式 时间函数特征 频率函数特征 连续时间傅立叶变换 (CFT) 连续 、非周期 非周期 、连续 连续时间傅立叶级数 (CFS) 连续 、周期 非周期 、离散 离散时间傅立叶变换 (DTFT) 离散 、非周期 周期 、连续 离散时间傅立叶级数 (DFS) 离散、周期 周期、离散 用于计算机处理有什么问题?

离散傅里叶变换及快速算法 主要内容 ◆>■周期序列的DFS及性质 离散傅里叶变换(DFT) 及性质 DFT的快速算法(FFT) DFT/FFT的应用
离散傅里叶变换及快速算法 主要内容 周期序列的DFS及性质 离散傅里叶变换(DFT)及性质 DFT的快速算法(FFT) DFT/FFT的应用

周期序列的DFS表达 rX(k)=DrSl=∑me京=∑mw N-1 2π N-1 a=DrR训=艺xeR-N艺Xaw, h=0 2π W- N k=0 N k=0 口理解频域自变量k的含义 n是对T的归一化,k是p对 的归一化 理解W、=e京的一些性质 2元 ▣ 共轭对称性W=(W") 周期性W=Wtv,为整数 可约性W秋=W,W=W,为整数 正交性空w-m
1 1 2 0 0 ( ) DFS[ ( )] ( ) ( ) N N j nk N n n nk X k xn xne xn WN 1 1 2 0 0 1 1 ( ) IDFS[ ( )] ( ) ( ) N N j nk N k k nk N xn Xk Xke Xk N W N 2 j N W e N 周期序列的DFS表达 * ( ) n n W W N N , n n iN WW i N N 为整数 / , , in n in n W W W Wi N N i Ni N 为整数 1 * 0 1 1, ( ) 0, N nk mk N N n n m iN W W N n m iN 共轭对称性 周期性 可约性 正交性 理解频域自变量 k 的含义 n 是 t 对 Ts 的归一化,k 是 w 对 的归一化 2 N 理解 的一些性质
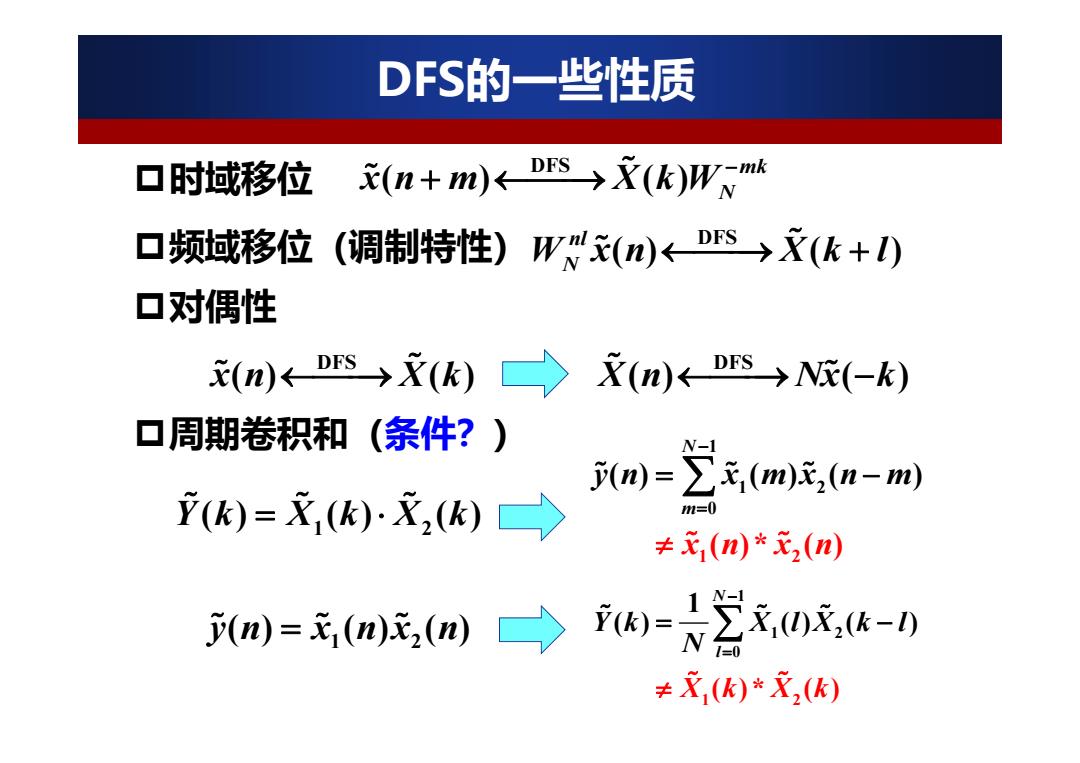
DFS的一些性质 ▣时域移位 (n+m)←s→(k)Wm ▣频域移位 (调制特性)W()←Ds→(k+) ▣对偶性 (n)KDs→(K)〉 (n)←s→N(-k) 口周期卷积和(条件?) N-I jm)=∑,(m)e,(n-m) ()=文(k)(k) =0 ≠x1(m)*x2(n) (n)=元(n)e,(m)〉 =2求x,-) ≠文(K)*文(K)
时域移位 DFS的一些性质 DFS ( ) () mk N xn m X kW 频域移位(调制特性) DFS () ( ) nl W xn Xk l N 对偶性 DFS x() () n Xk DFS X() ( ) n Nx k 周期卷积和(条件?) 1 2 Yk X k X k () () () 1 1 2 0 1 2 () ( ( )* ) ) ( ( ) N m y x n n xn x mx n m 1 2 y () () () n x nx n 0 2 1 1 1 2 1 ( ) () ( ) ( )* ( ) N l Yk X lX k l k Xk N X

离散傅里叶变换及快速算法 主要内容 周期序列的DFS及性质 ◆>■离散傅里叶变换(DFT)及性质 DFT的快速算法(FFT) aDFT/FFT的应用
离散傅里叶变换及快速算法 主要内容 周期序列的DFS及性质 离散傅里叶变换(DFT)及性质 DFT的快速算法(FFT) DFT/FFT的应用

离散傅里叶变换及性质 如果信号不是周期的,有没有办法利用计算机获 取/存储其时频域特征? 条件1:时域离散,有限长/周期 条件2:频域离散,有限长/周期 √ 时域有限,频域无限! 怎么办? 1构造周期信号 一信号周期延拓 (n)=∑x(n+rW)=x(n)N r=-00 有限长序列是周期信号 x(n)=(n)R (n) 的主值序列
离散傅里叶变换及性质 如果信号不是周期的,有没有办法利用计算机获 取/存储其时频域特征? 条件1:时域离散,有限长/周期 条件2:频域离散,有限长/周期 时域有限,频域无限! 怎么办? 构造周期信号 —— 信号周期延拓 () ( ) r x n x n rN () () () N x n xnR n 有限长序列是周期信号 的主值序列 (( )) N x n

离散傅里叶变换(DFT) ▣ DFT的定义 X)=兑mr 0≤k≤N-1 =0 注意N的含义 m=大2Xkwg40≤n≤N-1 周期! N k=0 ▣DFT与DFS的关系 x(n)=(n)R (n) DFT是DFS的主值序列 X(k)=x(k)Rv(k) (n)=x(n)) √DFS是DFT的周期延拓 ()=X(k)
1 0 1 0 ( ) ( ) 0 1 1 ( ) ( ) 0 1 N nk N n N nk N k X k x nW k N xn X kW n N N 离散傅里叶变换(DFT) 注意N的含义 DFT的定义 DFT与DFS的关系 DFT是DFS的主值序列 () () () () () () NN xn xnR n Xk XkR k DFS是DFT的周期延拓 NN xn x n Xk X k 周期!
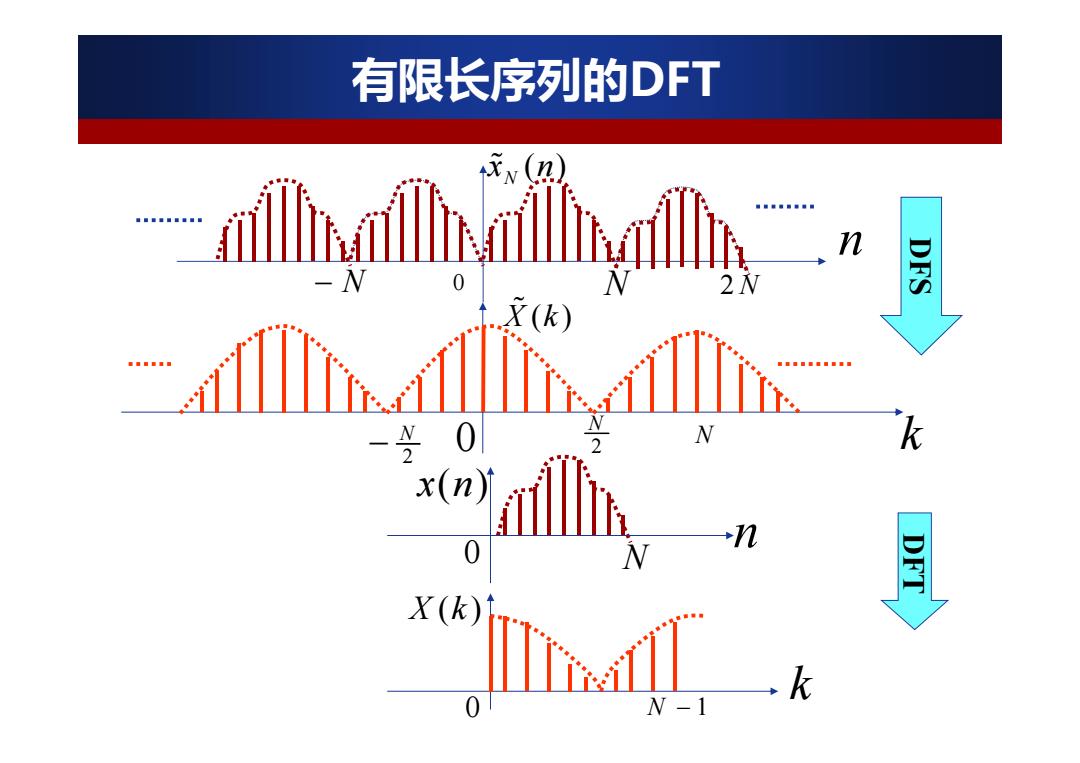
有限长序列的DFT n DFS X(k) ■■■■■ ■■■■■重■■■ N k x(n N n X(k) k 0 W-1
( ) N x n n N 0 N 2 N X ( ) k 0 2N N k 0 N n x(n) 0 N 1 k X (k ) DFS DFT 2N 有限长序列的DFT