
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC chapterd4fiteingintheFftegμegylonatin

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Outline Background Preliminary Concepts Sampling and the Fourier Transform of Sampled Functions The Discrete Fourier Transform of One Variable Extension to Functions of Two Variables Some Properties of the 2-D Discrete Fourier Transform The Basics of Filtering in the Frequency Domain Image Smoothing Using Frequency Domain Filters Image Sharpening Using Frequency Domain Filters Selective Filtering
Outline ◆ Background ◆ Preliminary Concepts ◆ Sampling and the Fourier Transform of Sampled Functions ◆ The Discrete Fourier Transform of One Variable ◆ Extension to Functions of Two Variables ◆ Some Properties of the 2-D Discrete Fourier Transform ◆ The Basics of Filtering in the Frequency Domain ◆ Image Smoothing Using Frequency Domain Filters ◆ Image Sharpening Using Frequency Domain Filters ◆ Selective Filtering

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 4.1 Background Agenda A Brief History of the Fourier Series and Transform
A Brief History of the Fourier Series and Transform 4.1 Background Agenda

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History Jean Baptiste Joseph Fourier: French mathematician,born in 1768 in the town of Auxerre. ■ Fourier's contribution states that any periodic function can be expressed as the sum of sines and/or cosines of different frequencies,each multiplied by a different coefficient (we now Fourier(1768-1830) call this sum a Fourier series)
A Brief History ◼ Jean Baptiste Joseph Fourier: French mathematician, born in 1768 in the town of Auxerre. ◼ Fourier’s contribution states that any periodic function can be expressed as the sum of sines and/or cosines of different frequencies, each multiplied by a different coefficient (we now call this sum a Fourier series). Fourier(1768 –1830)
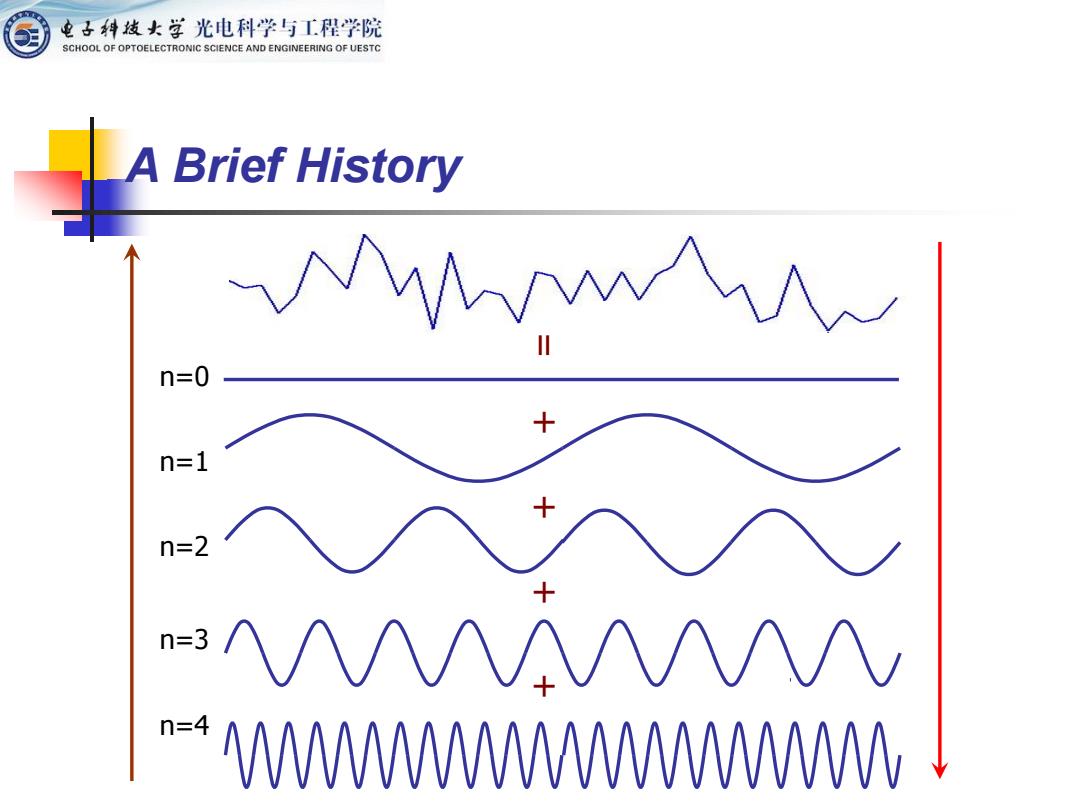
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History w n=0 × n=1 n=2 n=3 n=4 WWWM
= + + + + n=0 n=1 n=2 n=3 n=4 A Brief History

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Outline Background Preliminary Concepts Sampling and the Fourier Transform of Sampled Functions The Discrete Fourier Transform of One Variable Extension to Functions of Two Variables Some Properties of the 2-D Discrete Fourier Transform The Basics of Filtering in the Frequency Domain ◆ Image Smoothing Using Frequency Domain Filters Image Sharpening Using Frequency Domain Filters Selective Filtering
Outline ◆ Background ◆ Preliminary Concepts ◆ Sampling and the Fourier Transform of Sampled Functions ◆ The Discrete Fourier Transform of One Variable ◆ Extension to Functions of Two Variables ◆ Some Properties of the 2-D Discrete Fourier Transform ◆ The Basics of Filtering in the Frequency Domain ◆ Image Smoothing Using Frequency Domain Filters ◆ Image Sharpening Using Frequency Domain Filters ◆ Selective Filtering

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 4.1 Preliminary Concepts Agenda Complex Numbers Fourier Series Impulses and Their Sifting Property The Fourier Transform of Functions of One Continuous variable Convolution
Complex Numbers Fourier Series Impulses and Their Sifting Property The Fourier Transform of Functions of One Continuous Variable Convolution 4.1 Preliminary Concepts Agenda

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 1.Complex numbers A complex number,C,is defined as C=R+i1,C'=R-il Representation of complex numbers in polar coordinates C=C(cos0+jsine) where C=VR2+12
* C R I C R I = + = − j , j ◆ A complex number, C, is defined as 1. Complex numbers ◆ Representation of complex numbers in polar coordinates C C j = + ( cos sin ) where 2 2 C R I = +

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 1.Complex numbers Euler's formula Leonhard Euler(1707-1783) e=cos0+jsin Representation of complex numbers in polar coordinates C=Cle A pioneering Swiss mathematician and physicist.He made important discoveries in fields as diverse as infinitesimal calculus and graph theory.He also introduced much of the modern mathematical terminology and notation,particularly for mathematical analysis,such as the notion of a mathematical function.He is also renowned for his work in mechanics,fluid dynamics,optics,astronomy,and music theory
cos sin j e j = + ◆ Euler’s formula ◆ Representation of complex numbers in polar coordinates Leonhard Euler(1707-1783) j C C e = 1. Complex numbers A pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function. He is also renowned for his work in mechanics, fluid dynamics, optics, astronomy, and music theory

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 2.Fourier Series ◆Fourier series Fourier Series can be expressed as the sum of sines and cosines multiplied by appropriate coefficients. 2πn f0=∑ce n=-00 where c,7打f0y守an-nL2 2πn
( ) 2 n j t T n n f t c e =− = Fourier Series can be expressed as the sum of sines and cosines multiplied by appropriate coefficients. 2. Fourier Series where ( ) 2 2 2 1 , 0, 1, 2,... n T j t T n T c f t e dt n T − = = ◆ Fourier Series