
IR数字滤波器设计 刘科 自动化工程学院
IIR数字滤波器设计 刘科 自动化工程学院

IR数字滤波器设计 主要内容 ◆>口数字滤波器的设计过程 ▣川R数字滤波器的设计
IIR数字滤波器设计 主要内容 数字滤波器的设计过程 IIR数字滤波器的设计

数字滤波器的设计过程 ▣ 表征:按设计任务,确定滤波器性能要求,用特 定的技术指标对其进行表征 口求解:用离散LT系统的系统函数H(z)(频率响应) 逼近所需的性能指标(计算系数) 因果稳定 口设计:实现此系统函数 有限精度算法:如运算结构、字长的选择、码制等 口实现:实际技术实现 软件法、硬件法或DSP芯片法
求解:用离散LTI系统的系统函数H(z)(频率响应) 逼近所需的性能指标(计算系数) 表征:按设计任务,确定滤波器性能要求,用特 定的技术指标对其进行表征 设计:实现此系统函数 实现:实际技术实现 数字滤波器的设计过程 因果稳定 有限精度算法:如运算结构、字长的选择、码制等 软件法、硬件法或DSP芯片法
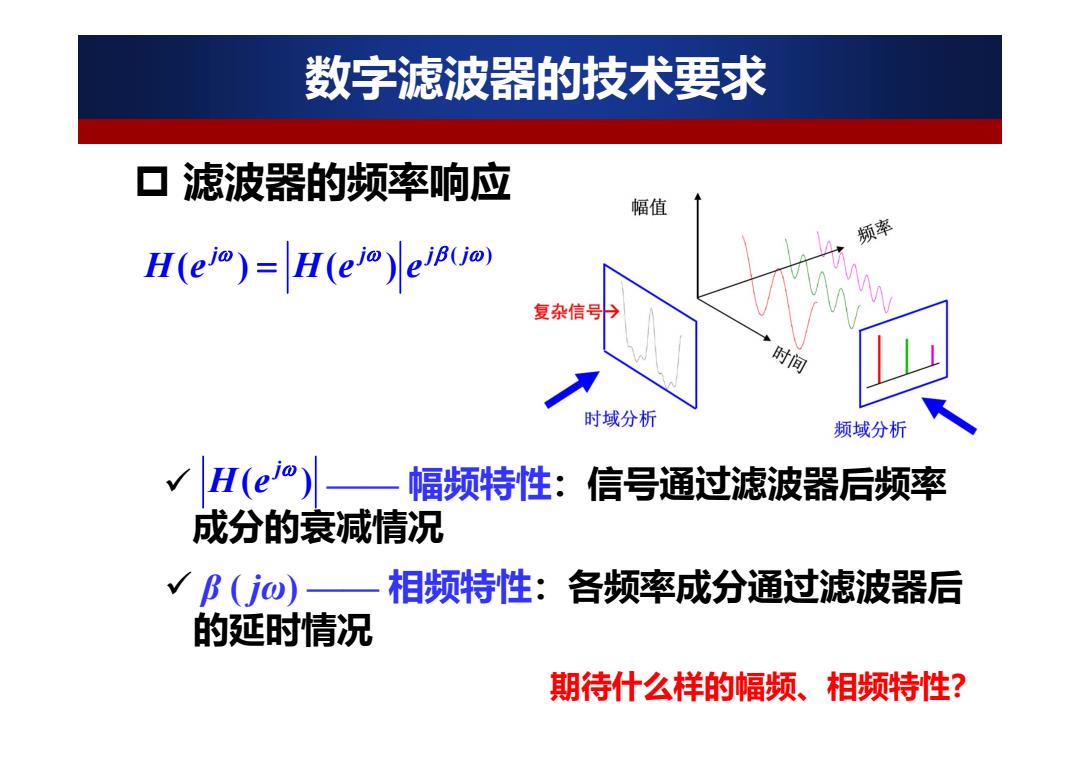
数字滤波器的技术要求 口滤波器的频率响应 幅值 频率 H(e)=H(el) 复杂信号书 时间 时域分析 频域分析 √H(o)一幅频特性:信号通过滤波器后频率 成分的衰减情况 B(jo) 一相频特性:各频率成分通过滤波器后 的延时情况 期待什么样的幅频、相频特性?
数字滤波器的技术要求 滤波器的频率响应 ( ) () () j j jj He He e —— 幅频特性:信号通过滤波器后频率 成分的衰减情况 ( ) j H e β ( j ω) —— 相频特性:各频率成分通过滤波器后 的延时情况 期待什么样的幅频、相频特性?
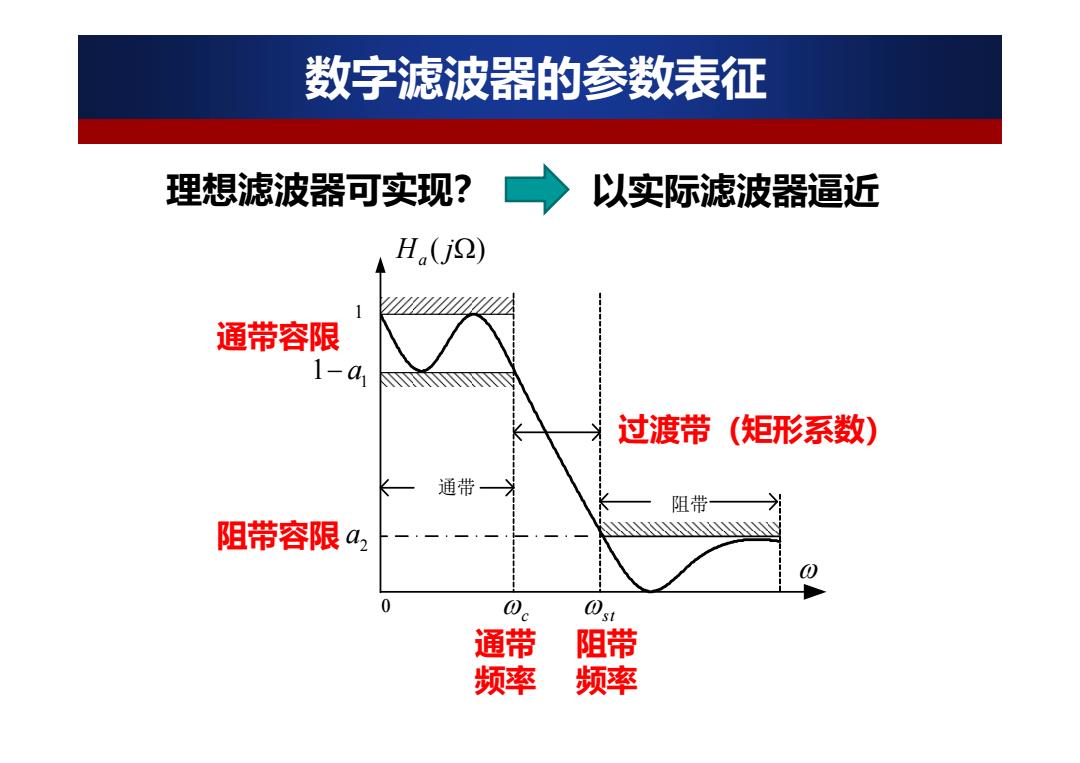
数字滤波器的参数表征 理想滤波器可实现? 以实际滤波器逼近 H(j2) 通带容限 1-a1 过渡带 (矩形系数) 通带 阻带 阻带容限a, 0 Q. 通带 阻带 频率 频率
阻带 频率 通带 频率 理想滤波器可实现? 通带 过渡带 阻带 ( ) H j a 1 1 a 2 a c st 数字滤波器的参数表征 以实际滤波器逼近 通带容限 阻带容限 过渡带(矩形系数)

IR数字滤波器设计 主要内容 ▣数字滤波器的设计过程 ◆>口R数字滤波器的设计
IIR数字滤波器设计 主要内容 数字滤波器的设计过程 IIR数字滤波器的设计
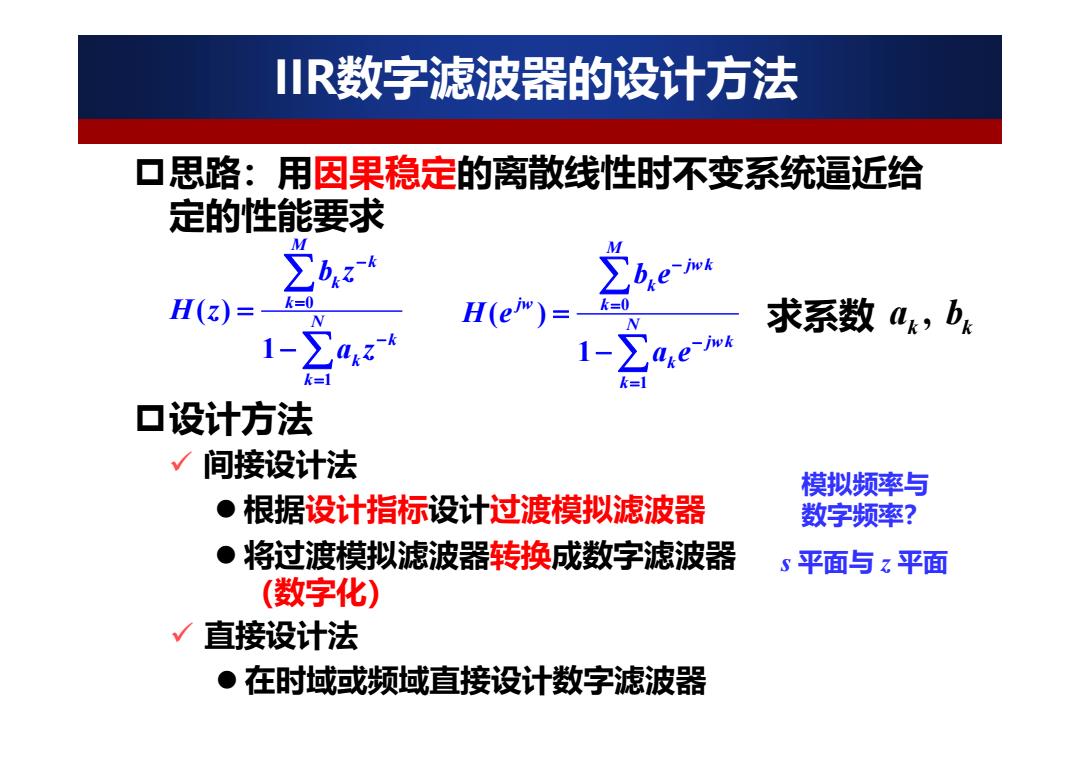
IR数字滤波器的设计方法 思路:用因果稳定的离散线性时不变系统逼近给 定的性能要求 M bre H(z)= k=0 H(e)= k=0 arz-k 1-∑a4em 求系数ak,b: 口设计方法 √间接设计法 模拟频率与 ●根据设计指标设计过渡模拟滤波器 数字频率? 将过渡模拟滤波器转换成数字滤波器 S平面与z平面 (数字化) 直接设计法 。在时域或频域直接设计数字滤波器
IIR数字滤波器的设计方法 0 1 ( ) 1 M k k k N k k k b z H z a z , k k 求系数 a b 思路:用因果稳定的离散线性时不变系统逼近给 定的性能要求 0 1 ( ) 1 M jwk k jw k N jwk k k b e H e a e 设计方法 间接设计法 根据设计指标设计过渡模拟滤波器 将过渡模拟滤波器转换成数字滤波器 (数字化) 直接设计法 在时域或频域直接设计数字滤波器 模拟频率与 数字频率? s 平面与 z 平面
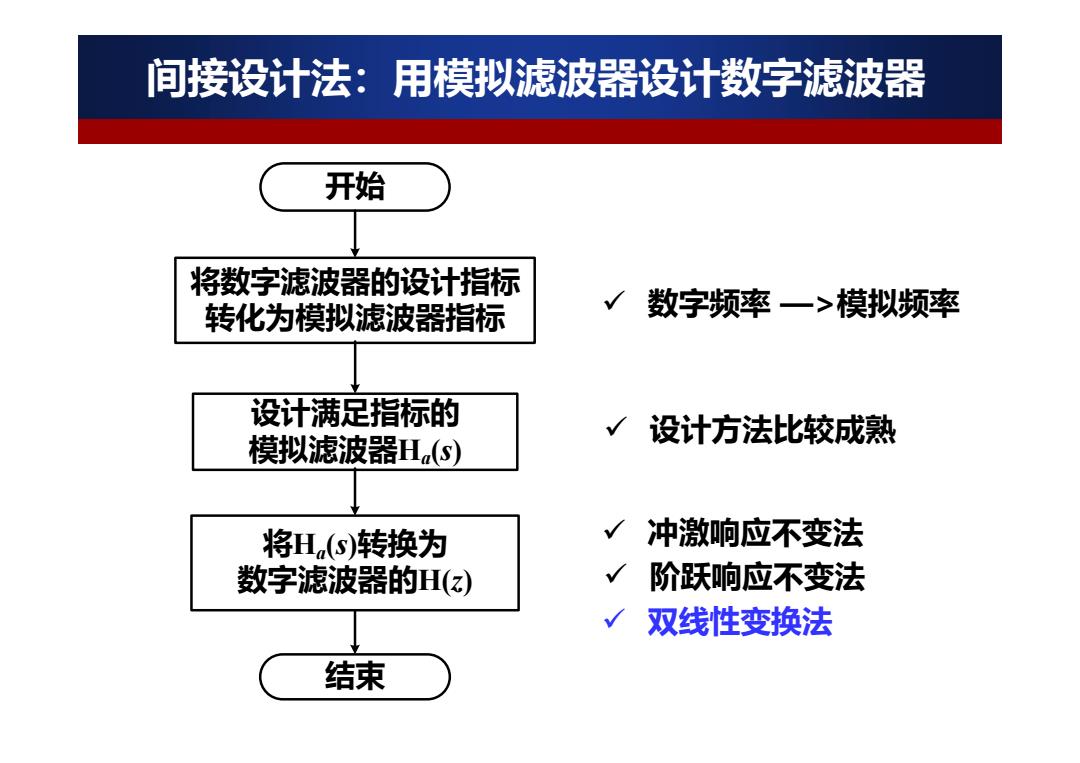
间接设计法:用模拟滤波器设计数字滤波器 开始 将数字滤波器的设计指标 转化为模拟滤波器指标 √数字频率一>模拟频率 设计满足指标的 √设计方法比较成熟 模拟滤波器Hs) 将H(s)转换为 √冲激响应不变法 数字滤波器的H(z) √ 阶跃响应不变法 √双线性变换法 结束
冲激响应不变法 阶跃响应不变法 双线性变换法 开始 将数字滤波器的设计指标 转化为模拟滤波器指标 设计满足指标的 模拟滤波器Ha(s) 结束 将Ha(s)转换为 数字滤波器的H(z) 间接设计法:用模拟滤波器设计数字滤波器 数字频率 —>模拟频率 设计方法比较成熟
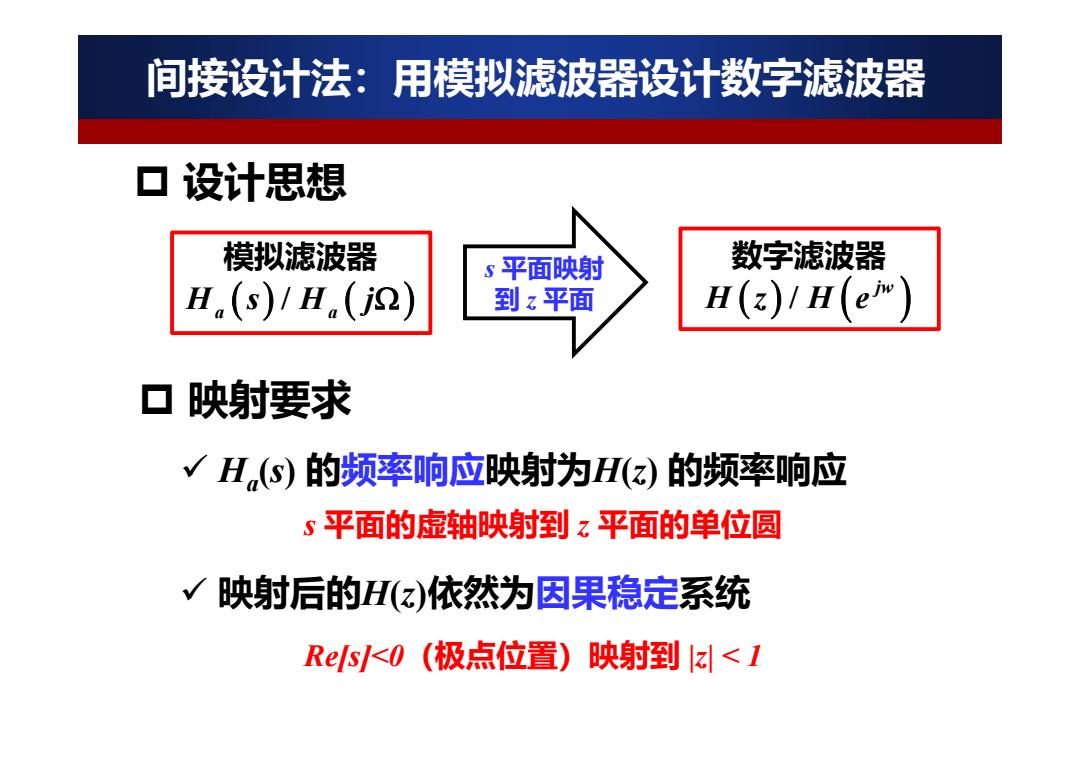
间接设计法:用摸拟滤波器设计数字滤波器 口设计思想 模拟滤波器 5平面映射 数字滤波器 H.(s)1H.(j2) 到z平面 H(z)/H(e) 口映射要求 √H,(S)的频率响应映射为H(z)的频率响应 s平面的虚轴映射到z平面的单位圆 √映射后的H(z)依然为因果稳定系统 RsK0(极点位置)映射到z<1
间接设计法:用模拟滤波器设计数字滤波器 设计思想 Ha ( s) 的频率响应映射为 H( z) 的频率响应 Re[s]<0(极点位置)映射到 |z| < 1 映射要求 模拟滤波器 / H a a sHj 数字滤波器 / jw H z He s 平面映射 到 z 平面 s 平面的虚轴映射到 z 平面的单位圆 映射后的 H( z )依然为因果稳定系统

回顾s域与z域的关系 20 00 i(t)=h,()∑δ(t-nT)F∑h(nT)6(t-nT) 1c i()=于∑H,(s-jm,)∑al(n)er 10 1=o0 H(a)=2()2-=A.(=∑A((s-2,) 1=o0 口序列的z变换与模拟信号的抽样信号的拉氏变换是一对一 变换关系 口序列的z变换与模拟信号的拉氏变换是多值映射关系(间 隔为?、的频点,共同组成z变换的一个点) 究竟怎么映射?
回顾 s 域与 z 域的关系 ˆa a = n n h t h t t nT h nT t nT 1 ˆ = snT a as n n H s H s jn h n e T 1 = ˆ a z esT a n s n n H z hn H T z s H s jn 序列的 z 变换与模拟信号的抽样信号的拉氏变换是一对一 变换关系 序列的 z 变换与模拟信号的拉氏变换是多值映射关系(间 隔为Ωs 的频点,共同组成 z 变换的一个点) 究竟怎么映射?