
956 全局优化算法在天线阵综合 中的应用
全局优化算法在天线阵综合 中的应用

粒子群算法 1956 粒子群算法(PS0)介绍 Ref.Daniel W.Boeringer and Douglas H.Werner,"Particle Swarm Optimization Versus Genetic Algorithms for Phased Array Synthesis",IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION,VOL.52,NO.3,MARCH 2004
粒子群算法 粒子群算法(PSO)介绍 Ref. Daniel W. Boeringer and Douglas H. Werner, “Particle Swarm Optimization Versus Genetic Algorithms for Phased Array Synthesis”, IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION, VOL. 52, NO. 3, MARCH 2004

粒子群算法 1956 产生背景 粒子群算法(Particle Swarm Optimization)由Kennedy和 Eberhart在1995年提出,该算法对于Hepper的模拟鸟群(鱼群) 的模型进行修正,以使粒子能够飞向解空间,并在最好解处 降落,从而得到了粒子群优化算法。 设想这样一个场景:一群鸟在随机的搜索食物。在这个区域 里只有一块食物,所有的鸟都不知道食物在哪。但是它们知 道自己当前的位置距离食物还有多远。 那么找到食物的最优策略是什么? 最简单有效的就是搜寻目前离食物最近的鸟的周围区域
粒子群算法( Particle Swarm Optimization )由Kennedy和 Eberhart在1995年提出,该算法对于Hepper的模拟鸟群(鱼群) 的模型进行修正,以使粒子能够飞向解空间,并在最好解处 降落,从而得到了粒子群优化算法。 粒子群算法 设想这样一个场景:一群鸟在随机的搜索食物。在这个区域 里只有一块食物,所有的鸟都不知道食物在哪。但是它们知 道自己当前的位置距离食物还有多远。 最简单有效的就是搜寻目前离食物最近的鸟的周围区域。 那么找到食物的最优策略是什么? 产生背景

粒子群算法 1988 数学模型 假设在一个D维搜索空间中,有m个粒子组成一粒子群; 其中第i个粒子的空间位置为X:=(x1x2,x3,…,xD),i=1,2,…,m 它是优化问题的一个潜在解; ■ 将它带入优化目标函数可以计算出其相应的适应值;根 据适应值可衡量的优劣; 第个粒子所经历的最好位置称为其个体历史最好位置, 记为obest,.相应的适应值为个体最好适应值Fi; ■ 同时,每个粒子还具有各的飞行速 度V=(v1,v2,V3,…,VD),i=1,2,…m。 所有粒子经历过的位置中的最好位置称为全局历史最好 位置,记为gbest
假设在一个D维搜索空间中,有m个粒子组成一粒子群; 其中第i 个粒子的空间位置为 它是优化问题的一个潜在解; 将它带入优化目标函数可以计算出其相应的适应值;根 据适应值可衡量的优劣; 第i个粒子所经历的最好位置称为其个体历史最好位置, 记为pbest,相应的适应值为个体最好适应值 Fi ; 同时,每个粒子还具有各的飞行速 度 。 所有粒子经历过的位置中的最好位置称为全局历史最好 位置,记为gbest。 粒子群算法 数学模型 𝑋𝑖 = (𝑥𝑖1, 𝑥𝑖2, 𝑥𝑖3, ⋯ , 𝑥𝑖𝐷), 𝑖 = 1,2, ⋯ , 𝑚 𝑉𝑖 = (𝑣𝑖1, 𝑣𝑖2, 𝑣𝑖3, ⋯ , 𝑣𝑖𝐷), 𝑖 = 1,2, ⋯ 𝑚

粒子群算法 1956 算法简介 每个寻优的问题解都被想像成一只鸟,称为“粒子”。所有 粒子都在一个D维空间进行搜索。 所有的粒子都由一个fitness-function确定适应值以判断目前 的位置好坏。 ■每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。 每一个粒子还有一个速度以决定飞行的距离和方向。这个速 度根据它本身的飞行经验以及同伴的飞行经验进行动态调整
每个寻优的问题解都被想像成一只鸟,称为“粒子”。所有 粒子都在一个D维空间进行搜索。 所有的粒子都由一个fitness-function确定适应值以判断目前 的位置好坏。 每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。 每一个粒子还有一个速度以决定飞行的距离和方向。这个速 度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。 粒子群算法 算法简介

粒子群算法 956 速度更新函数 Via=wxVa+C xrandO(Pa-Xa(t))+C2xrandOx(Psd-Xa(t)) Va:第i个particle(有d个维度)的速度 Pd:每个particle到目前为止所出现的最佳位置 口Pa:所有particle到目前为止所出现的最佳位置 OXa:每个particle目前的所在位置 ■C,C2:学习常数 ☐w:惯性权重 位置更新函数 ☐rand0:0~1之间的随机数 Xid Xid Vid
粒子群算法 V w V C rand P X t C rand P X t id id id id gd id 1 2 () () Vid:第 i 个 particle (有d个维度) 的速度 Pid:每个particle 到目前为止所出现的最佳位置 Pgd:所有 particle 到目前为止所出现的最佳位置 Xid:每个 particle 目前的所在位置 C1 ,C2:学习常数 w:惯性权重 rand():0~1之间的随机数 速度更新函数 𝑋𝑖𝑑 = 𝑋𝑖𝑑 + 𝑉𝑖𝑑 位置更新函数
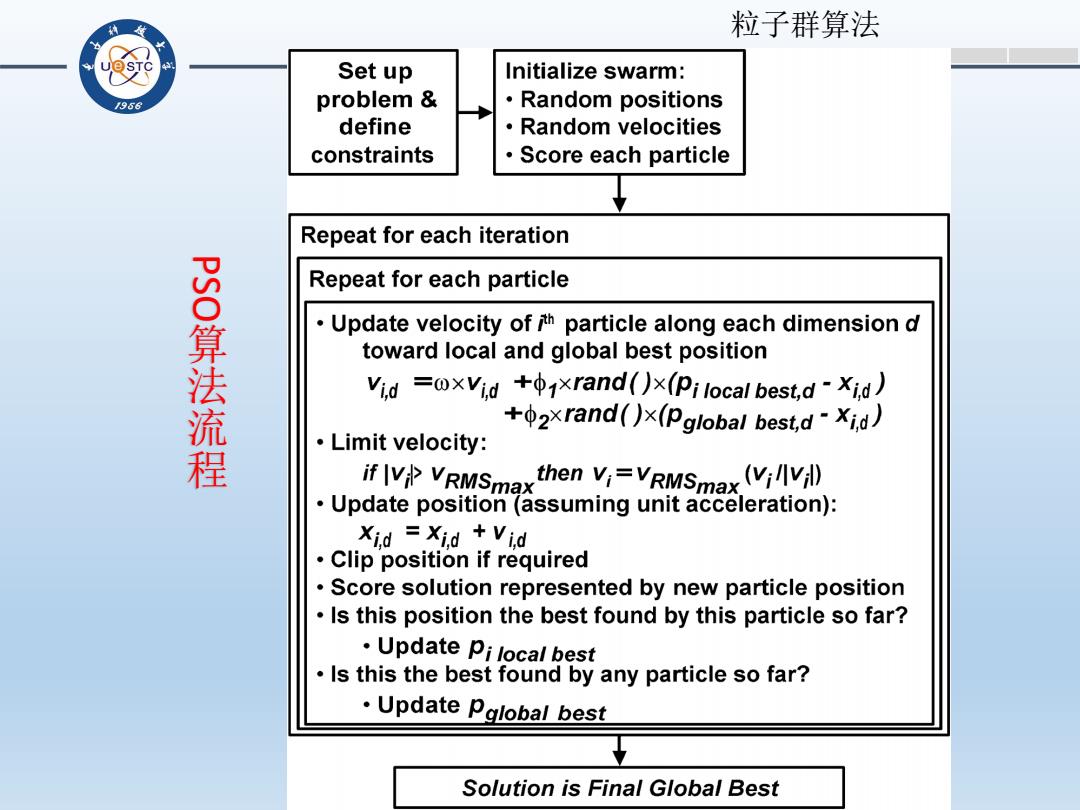
粒子群算法 Set up Initialize swarm: 956 problem ·Random positions define ·Random velocities constraints Score each particle Repeat for each iteration Repeat for each particle PSo算法流程 Update velocity of ith particle along each dimension d toward local and global best position Vid =xVid xrand()x(Pilocal bestd-Xid) +2xrand()x(Pglobal best,d-Xid) Limit velocity: if IV VRMSmaxthen V,=VRMSmax (viv Update position (assuming unit acceleration): Xid Xid +Vid Clip position if required Score solution represented by new particle position Is this position the best found by this particle so far? Update pi local best Is this the best found by any particle so far? ·Update Pglobal best Solution is Final Global Best
粒子群算法 PSO 算法流程

粒子群算法 1956 粒子群算法的改进 1997年 Kennedy和Eberhart提出了二进制PSO算法 1998年 Shi和Eberhart引入了惯性权重w,并提出动态调整惯性权重以平衡收 敛的全局性和收敛速度,该算法被称为标准P$O算法 1999年 Clerc引入收缩因子以保证算法的收敛性 1999年 Angeline将进化计算中的选择概念引入到PSO算法中 Lovbjerg?等人将进化计算中的复制、交叉等机制应用于PSO算法 1999年 Suganthan在标准PSO算法中引入了空间邻域的概念,将处于同一个 空间领域的粒子构成一个子粒子群分别进行进化,并随着进化动态 地改变选择阈值以保证群体的多样性 1999年 Kennedy引入邻域拓扑的概念来调整邻域的动态选择,并引入社会信 念将空间邻域与邻域拓扑中地环拓扑相结合以增加邻域间地信息交 流,提高群体的多样性 2001年 Lovbjerg等人将遗传算法中的子群体概念引入PSO算法中,同时引入 繁殖算子以进行子群体的信息交流
粒子群算法 粒子群算法的改进 1997年 Kennedy和Eberhart提出了二进制PSO算法 1998年 Shi和Eberhart引入了惯性权重w,并提出动态调整惯性权重以平衡收 敛的全局性和收敛速度,该算法被称为标准PSO算法 1999年 Clerc引入收缩因子以保证算法的收敛性 1999年 Angeline将进化计算中的选择概念引入到PSO算法中 Lovbjerg等人将进化计算中的复制、交叉等机制应用于PSO算法 1999年 Suganthan在标准PSO算法中引入了空间邻域的概念,将处于同一个 空间领域的粒子构成一个子粒子群分别进行进化,并随着进化动态 地改变选择阈值以保证群体的多样性 1999年 Kennedy引入邻域拓扑的概念来调整邻域的动态选择,并引入社会信 念将空间邻域与邻域拓扑中地环拓扑相结合以增加邻域间地信息交 流,提高群体的多样性 2001年 Lovbjerg等人将遗传算法中的子群体概念引入PSO算法中,同时引入 繁殖算子以进行子群体的信息交流

遗传算法 956 遗传算法(GA)介绍
遗传算法 遗传算法(GA)介绍

遗传算法 1956 原理简介 >遗传算法(G)是模拟生物在自然环境下的遗传和进化过程而形成的 一种自适应全局优化概率搜索方法。其采纳了自然进化模型,从 代表问题可能潜在解集的一个种群开始,种群由经过基因编码的 一定数目的个体组成。每个个体实际上是染色体带有特征的实体; 初始种群产生后,按照适者生存和优胜劣汰的原理,逐代演化产 生出越来越好的解: ·在每一代,概据问题域中个体的适应度大小挑选个体; 并借助遗传算子进行组合交叉和主客观变异,产生出代表新的解集的 种群。 。 这一过程循环执行,直到满足优化准则为止。最后,末代个体经解码, 生成近似最优解。 >基于种群进化机制的遗传算法如同自然界进化一样,后生代种群 比前生代更加适应于环境,通过逐代进化,逼近最优解
原理简介 遗传算法(GA)是模拟生物在自然环境下的遗传和进化过程而形成的 一种自适应全局优化概率搜索方法。其采纳了自然进化模型,从 代表问题可能潜在解集的一个种群开始,种群由经过基因编码的 一定数目的个体组成。每个个体实际上是染色体带有特征的实体; 初始种群产生后,按照适者生存和优胜劣汰的原理,逐代演化产 生出越来越好的解: • 在每一代,概据问题域中个体的适应度大小挑选个体; • 并借助遗传算子进行组合交叉和主客观变异,产生出代表新的解集的 种群。 • 这一过程循环执行,直到满足优化准则为止。最后,末代个体经解码, 生成近似最优解。 基于种群进化机制的遗传算法如同自然界进化一样,后生代种群 比前生代更加适应于环境,通过逐代进化,逼近最优解。 遗传算法