
FIR数字滤波器设计 刘科 自动化工程学院
FIR数字滤波器设计 刘科 自动化工程学院

IIR数字滤波器与FIR数字滤波器 ▣R数字滤波器 √容易不稳定 √相位非线性一用于宽带信号前必须校正相位 √相同性能下,阶次比FR滤波器要低得多 √可利用模拟滤波器设计 ▣FR数字滤波器 √因果稳定系统 √可严格线性相位,可任意幅度特性 √可用FFT计算
IIR数字滤波器与FIR数字滤波器 IIR数字滤波器 可利用模拟滤波器设计 相位非线性——用于宽带信号前必须校正相位 FIR数字滤波器 可严格线性相位,可任意幅度特性 因果稳定系统 可用FFT计算 相同性能下,阶次比FIR滤波器要低得多 容易不稳定

FR数字滤波器的设计方法 主要内容 ◆>1线性相位FR数字滤波器的特点 ·2窗函数设计法 ■3R与FR数字滤波器的比较
FIR数字滤波器的设计方法 主要内容 1 线性相位FIR数字滤波器的特点 2 窗函数设计法 3 IIR与FIR数字滤波器的比较

线性相位FR滤波器的特点 口FR滤波器的单位冲激响应(有限长、因果) h(n0≤n≤N-1 ▣系统函数 W-1 H(z)=∑(m)z" h=0 在z平面有N-1个零点 在z=0处是N-1阶极点
线性相位FIR滤波器的特点 FIR滤波器的单位冲激响应(有限长、因果) hn n N () 0 1 1 0 () () N n n H z hnz 系统函数 在 z 平面有N –1 个零点 在 z = 0 处是N –1 阶极点

线性相位条件 h(n)的频率响应、 频率相位函践幅度函数 N-1 H(e)=∑hm)er=H(o)eoo=±H(eleo, 1=0 相位函数 =H(e)eo 线性相位:(o)是ω的线性函数 群延时:一 (@)=t do 第一类线性相位:(0)=-0 第二类线性相位:(o)=B,-tω 如何才能实现?
h(n)的频率响应、频率/相位函数 一、线性相位条件 ( ) ( ) j j He e 群延时: d ( ) d 0 第二类线性相位:( ) 第一类线性相位:( ) 1 0 ( ) () N j j n n jw j w He hne He e ( ) ( ) j H e 线性相位: 是 的线性函数 幅度函数 相位函数 如何才能实现?

线性相位条件 第一类线性相位:0(o)=-o W-1 H(eo)=∑n)eom=±H(eo)leor t=0 ±Helo(or)-2(jos(on)sinor时_2aojs小n(am) n=( n=0 ±H(e)小sin(or)=∑(n)sin(on) cos(@r) ∑h(n)cos(on) n( ∑h(n)sin(or)cos(on)-∑(n)cos(@r)小sin(om)=0 如何满足? ∑(n)sin[(x-n)o]=0r
1 0 ( ) cos cos N j n He hn n 1 0 ( ) sin sin N j n He hn n 1 0 1 0 sin sin cos cos N n N n hn n hn n 1 1 0 0 sin cos cos sin 0 N N n n hn n hn n 1 0 sin 0 N n hn n 一、线性相位条件 第一类线性相位: 1 0 ( ) () ( ) N j j n j j n H e hne He e 如何满足? ( )
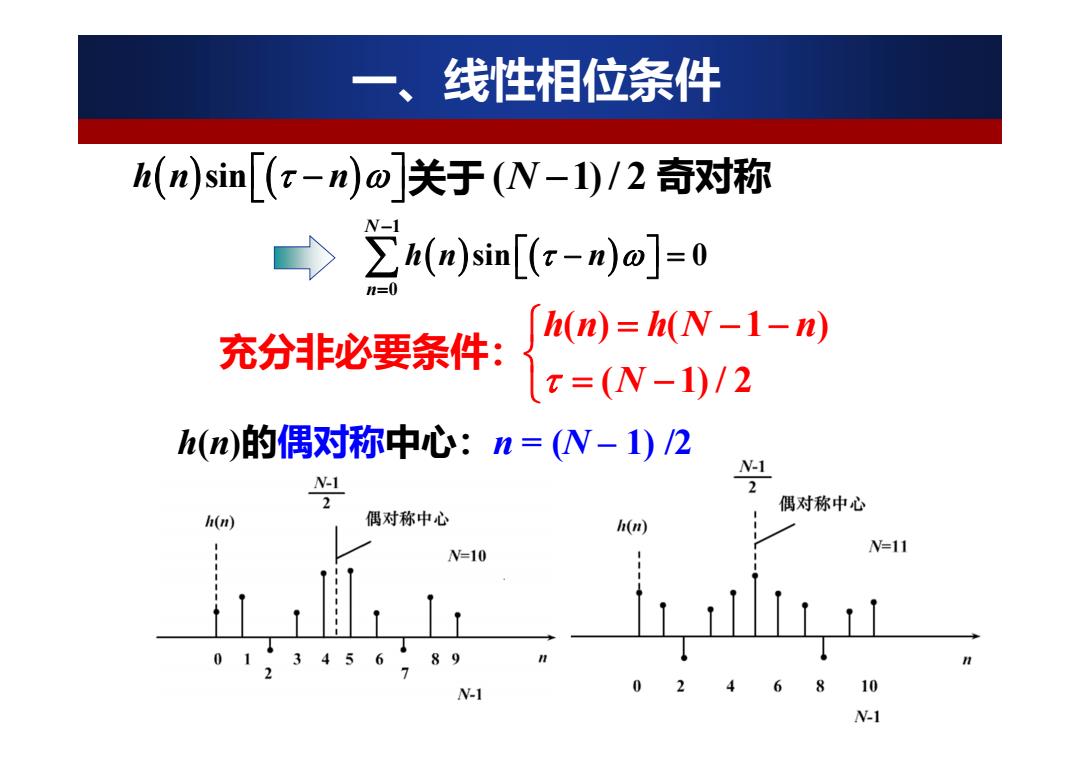
线性相位条件 h(n)sim[(x-n)o关于(N-l)/2奇对称 ∑h(n)sin[(x-n))o]=0 h(m)=h(N-1-n) 充分非必要条件: x=(N-1)/2 h(n)的偶对称中心:n=(N-1)/2 N-1 2 偶对称中心 h(n) 偶对称中心 h(n) N=10 W=11 456 89 10 N-1
h(n)的偶对称中心:n = (N – 1) /2 一、线性相位条件 充分非必要条件: () ( 1 ) ( 1) / 2 hn hN n N 1 0 sin 0 N n hn n hn n sin 关于 ( 1) / 2 N 奇对称
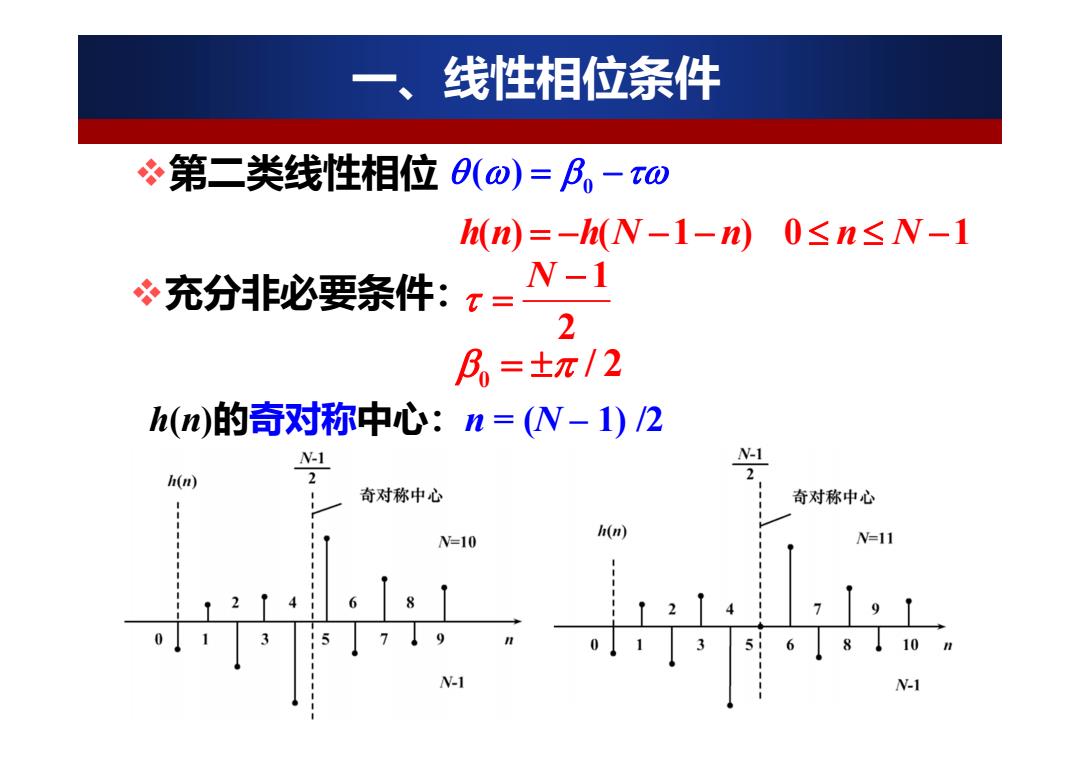
线性相位条件 第二类线性相位(o)=阝,-xo (n)=-(N-1-n0≤n≤N-1 充分非必要条件:x= N-1 2 =±π/2 h(n)的奇对称中心:n=(N-1)/2 N-1 N-1 h(n) 奇对称中心 奇对称中心 h(n =10 N=11 V-
第二类线性相位 0 ( ) hn hN n n N () ( 1 ) 0 1 1 2 N 0 / 2 h(n)的奇对称中心:n = (N – 1) /2 一、线性相位条件 充分非必要条件:

二、线性相位FIR滤波器频率响应的特点 分析频率响应,确定不同条件下滤波器的适用范围 h(n)=±h(N-1-n)0≤n≤N-1 He=∑dmg”=∑±uN-1-mz N- =0 =0 令m=N-1-n N-I H(z)=∑±h(m)zw-1m m=0 N-I =士z-w-∑mz" m=0 =±zN-DH(z1)
二、线性相位FIR滤波器频率响应的特点 1 1 0 0 () () ( 1 ) N N n n n n H z hnz hN nz 1 (1) 0 ( ) N N m m H z hmz ( 1) 1 ( ) N z H z 令mN n 1 hn hN n n N () ( 1 ) 0 1 1 ( 1) 0 ( ) N N m m z hmz 分析频率响应,确定不同条件下滤波器的适用范围

二、线性相位FR滤波器频率响应的特点 H(z)=±zN-DH(z) Ha)=[He)士&wHe] 2 wg±a2Aae W-1 =2[e±n] 1s0 N-1N-1 =2】 n=0 2
1 ( 1) 1 () () ( ) 2 N Hz Hz z Hz 1 1 ( 1) 0 0 1 () () 2 N N nN n n n hnz z hnz 1 ( 1) 0 1 ( ) 2 N n Nn n hn z z z 1 1 1 1 2 2 2 0 ( ) 2 N N n n N N n z z z hn ( 1) 1 ( ) N H z z Hz 二、线性相位FIR滤波器频率响应的特点