
Metamaterials with Negative Parameters:Physics and Applications
Metamaterials with Negative Parameters: Physics and Applications

Outline Theory Particle model Transmission Line model Effective Medium model Applications
Outline Theory Particle model Transmission Line model Effective Medium model Applications
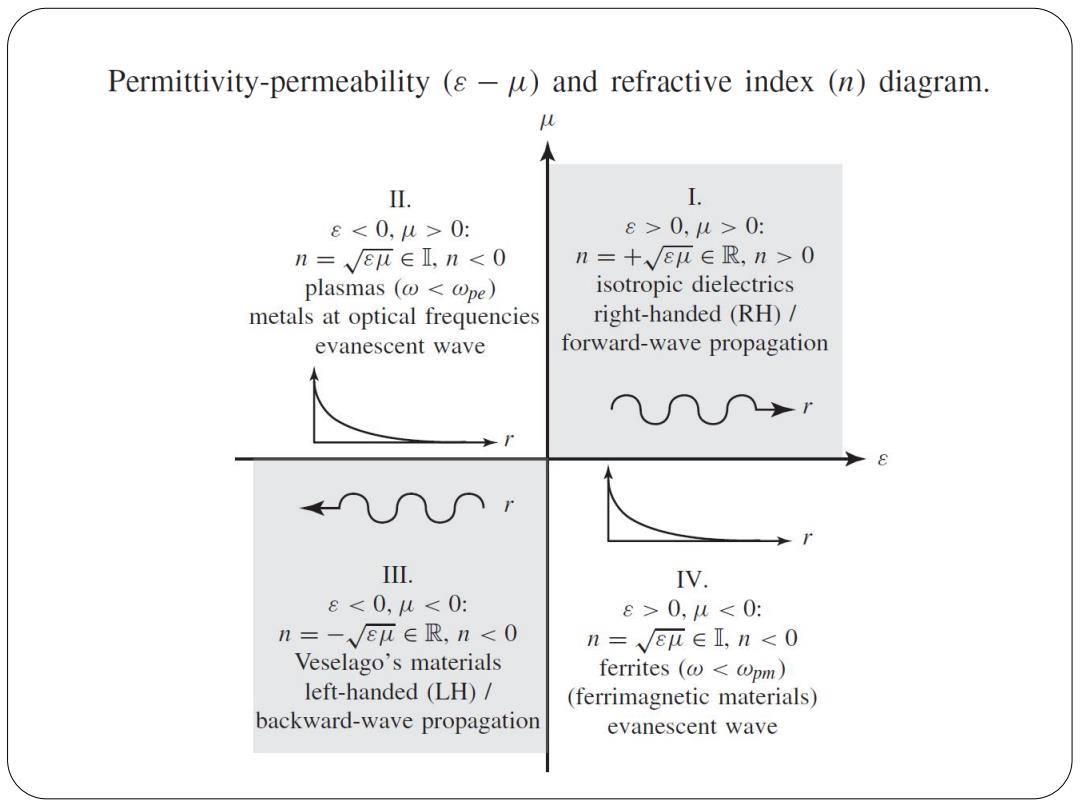
Permittivity-permeability (s-u)and refractive index (n)diagram. U II. I. e0: e>0,4>0: n=E∈L,n0 plasmas(ω0,u<0: n=-√E平∈R,n<0 n=√Eu∈I,n<0 Veselago's materials ferrites(ω<wpm) left-handed (LH)/ (ferrimagnetic materials) backward-wave propagation evanescent wave

TABLE 1.1.Verification of Main Properties and Fundamental Physics of LH MTMs by Different Approaches and Different Groups. Type of Investigation References Numerical FDTD Ziolkowski et al.[27,28] Numerical FEM Caloz et al.[29] Numerical TMA Markǒs et al.[20,21] Numerical TLM So and Hoefer [30,31] Theoretical EM Lindell et al.[32],Kong et al. [33,34],Smith et al..[35], McCall et al.[36] Experimental Shelby et al.[10],Greegor (bulk)TW-SRR et al.[22],Ziolkowski [26], Marques et al.[25]Tie Jun Cui Theoretical TL Eleftheriades et al.[37,38], Caloz and Itoh [39,40], 0 liner[41,42] Experimental Iyer et al.[43],Caloz and Itoh (planar)TL [40],Sanada et al.[44]
Tie Jun Cui

Dispersive model for the dielectric permittivity -Lorentz model (particle model) A.Lna H.A.Lorentz F=-e(E+v×B), The electron in an atom can be assumed to be bound to the equilibrium position through an elastic restoring force,the equation of motion is: mi+myi+mwor =-eEo exp(-iwt), Damping force due to all inelastic processes Harmonic restoring force r =ro exp(-iwt) -eEo/m w-w(w+iy)
Damping force due to all inelastic processes The electron in an atom can be assumed to be bound to the equilibrium position through an elastic restoring force, the equation of motion is: H.A.Lorentz Dispersive model for the dielectric permittivity ——Lorentz model (particle model) Harmonic restoring force
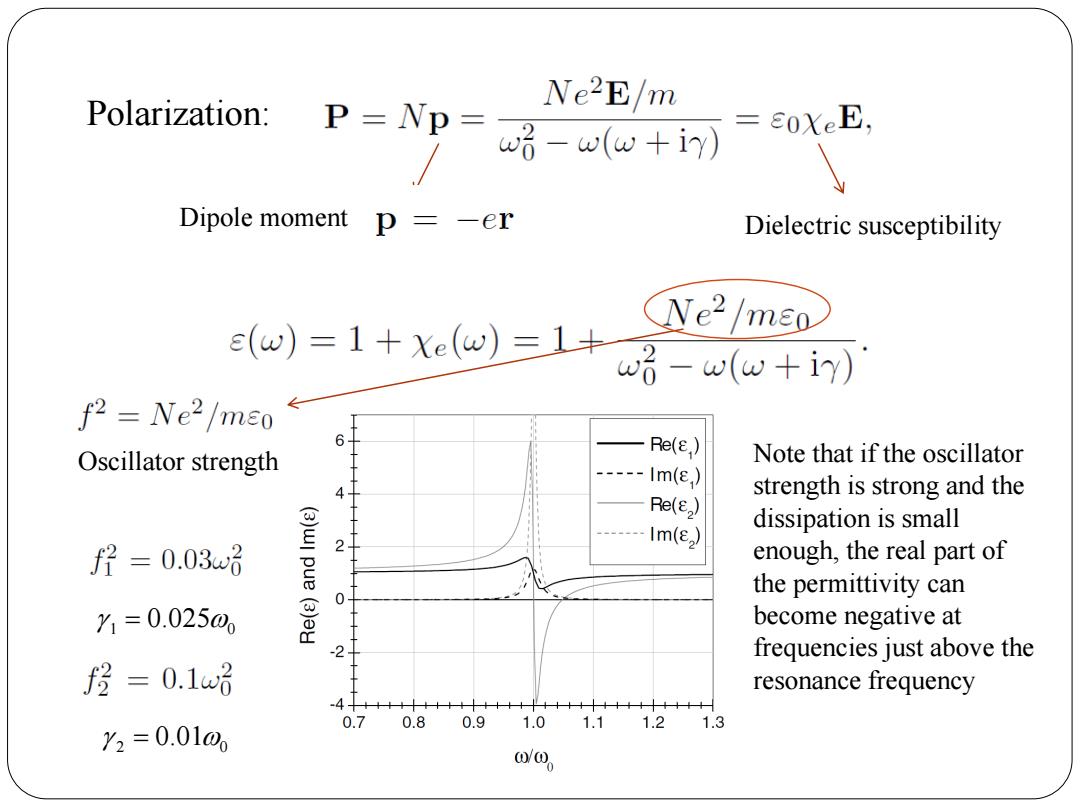
Ne2E/m Polarization: P=Np=略-w(w+in) =0XeE, Dipole moment p=-er Dielectric susceptibility Ne2/mEo e(w)=1+Xe(w)=1+ w话-w(w+iy) f2 Ne2/meo 6 Oscillator strength Re(E,) Note that if the oscillator --lm(e,) strength is strong and the Re() (3)wl dissipation is small Im() f= 0.03w 2 pue enough,the real part of the permittivity can ⊙ 0 1=0.02500 become negative at 正 -2 frequencies just above the f=0.1娟 resonance frequency =4 0.7 0.8 0.9 1.01.11.21.3 Y2=0.010 00
Polarization: Dipole moment Dielectric susceptibility Oscillator strength 1 0 0.025 2 0 0.01 Note that if the oscillator strength is strong and the dissipation is small enough, the real part of the permittivity can become negative at frequencies just above the resonance frequency
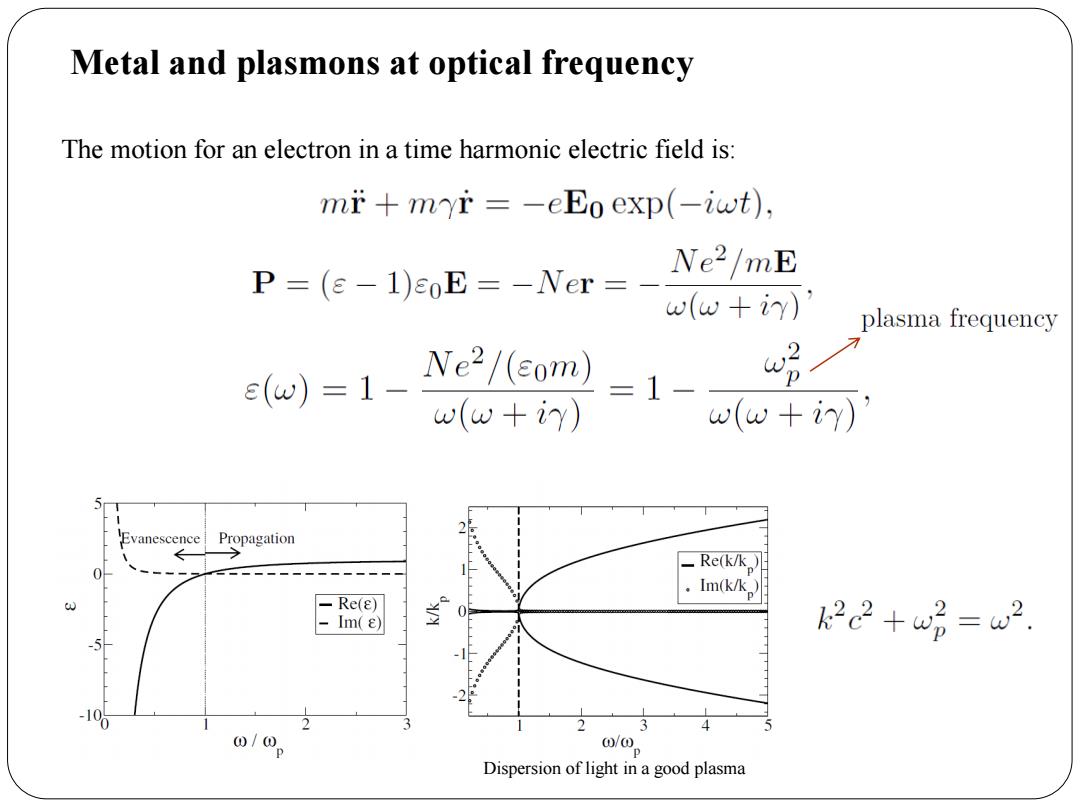
Metal and plasmons at optical frequency The motion for an electron in a time harmonic electric field is: mi+myi =-eEo exp(-iwt), P=(e-1)EoE--Ncr=_ e2/mE (w+iy) plasma frequency e(u)=1- Ne2/(com) w w(w+iy)】 -1- w(w+iy) Evanescence Propagation -Re(k/k。) 。 Im(k/k -Re(E) -Im() k2c2+w2=w2 10 2 3 00p 0/0. Dispersion of light in a good plasma
Metal and plasmons at optical frequency The motion for an electron in a time harmonic electric field is: Dispersion of light in a good plasma

Thin wire structures as low frequency negative permittivity (Pendry 1996) For many metals,the plasma frequency is at ultraviolet frequencies and y is small compared with.However,the dissipation in most metals is very large,so we have trouble when try to extend this behavior to low frequencies. In 1996,Pendry proposed that thin metallic wires behave as a low frequency plasma with a frequency stop-band from zero up to a cutoff frequency.The low frequency stop-band can be attributed to negative dielectric permittivity and the cutoff frequency to the plasma frequency. 个E
For many metals, the plasma frequency is at ultraviolet frequencies and is small compared with . However, the dissipation in most metals is very large, so we have trouble when try to extend this behavior to low frequencies. p Thin wire structures as low frequency negative permittivity (Pendry 1996) In 1996, Pendry proposed that thin metallic wires behave as a low frequency plasma with a frequency stop-band from zero up to a cutoff frequency. The low frequency stop-band can be attributed to negative dielectric permittivity and the cutoff frequency to the plasma frequency. E

Constraining electrons to move along thin wires has two consequences: 1.The average electron density is reduced because only part of space is filled by metal 元r2 neff a2 n, 2.The thin wires have a large self-inductance and it is not easy to change the currents flowing in them.So it appears as if the electrons had acquired a tremendously large mass H=品(日。) The vector potential associated with the field H(p)=67×A aoi=[nn] a yp< a-p =0 p 2 I=πr2nev r<a Approximation in the mean field limit A(p)≈lonr2neu 2π \p】
Constraining electrons to move along thin wires has two consequences: 1. The average electron density is reduced because only part of space is filled by metal 2. The thin wires have a large self-inductance and it is not easy to change the currents flowing in them. So it appears as if the electrons had acquired a tremendously large mass a I 1 0 ( ) H A The vector potential associated with the field Approximation in the mean field limit 0

We note that the canonical momentum of an electron in an electromagnetic field is p +eA.Thus assuming that the electrons flow on the surface of the wire (assuming a perfect conductor),we can associate a momentum per unit length of the wire of mentr2nv and thus an effective mass of uoπr2ne2 meff= 2元 we i() for the electron. Thus,assuming a longitudinal plasmonic mode for the system,we have neme2 2元c2 0p= Eomeff a2In(a/r) Typically one can chooser =1 um,a 10 mmand aluminium wires (n 1029 m-3), which gives an effective mass of mem=2.67×10-26kg, that is almost 15 times that of a proton,and a plasma frequency of about 2 GHz!Thus,we have succeeded in obtaining a negative dielectric material at microwave frequencies