
信号处理理论与算法 Vigner分布 张朋 自动化工程学院
信号处理理论与算法 Wigner分布 张 朋 自动化工程学院

Vigner分布的定义 时一频分布分类 ◆线性形式的时一频分布: STFT、Gabor?变换及小波变换。 ◆双线性形式时一频分布: 是指所研究的信号在时一频分布的数学表达式中以 相乘的形式出现两次。又称非线性时一频分布。Wigner 分布及Cohen类分布
线性形式的时-频分布: STFT、Gabor变换及小波变换。 双线性形式时-频分布: 是指所研究的信号在时-频分布的数学表达式中以 相乘的形式出现两次。又称非线性时-频分布。 Wigner 分布及Cohen类分布。 时—频分布分类 Wigner分布的定义

Vigner分布的定义 联合Wigner:分布时域定义 令信号x),y()的傅立叶变换分别是x(2),Y(2),那 么x(t),()的联合Wigner分布定义为: w,(t,)=x(t+7/2)y(1-7/2)e dr (3.1.1) 信号x(t)的自Wigner分布定义为: W (t,)=x(t+7/2)x'(t-7/2)edr (3.1.2) Wigner分布又称Wigner一Ville分布,简称为WVD。 若令/2=,则dr=2d,代入(3.1.1)有 Wx,(t,2)=2x(t+)y'(t-)e2d (3.1.3)
令信号 , 的傅立叶变换分别是 , ,那 么 , 的联合Wigner分布定义为: (3.1.1 ) 信号 的自Wigner分布定义为: (3.1.2 ) Wigner分布又称Wigner -Ville分布,简称为WVD 。 若令 ,则 ,代入(3.1.1)有 (3.1.3 ) x t y t X j Y j x t y t * , , 22 j W t xt x y y t ed x t * , 22 j W t xt x t e d x 2 d d 2 2 , , 2 j W t xt y t e d x y 联合Wigner分布时域定义 Wigner分布的定义
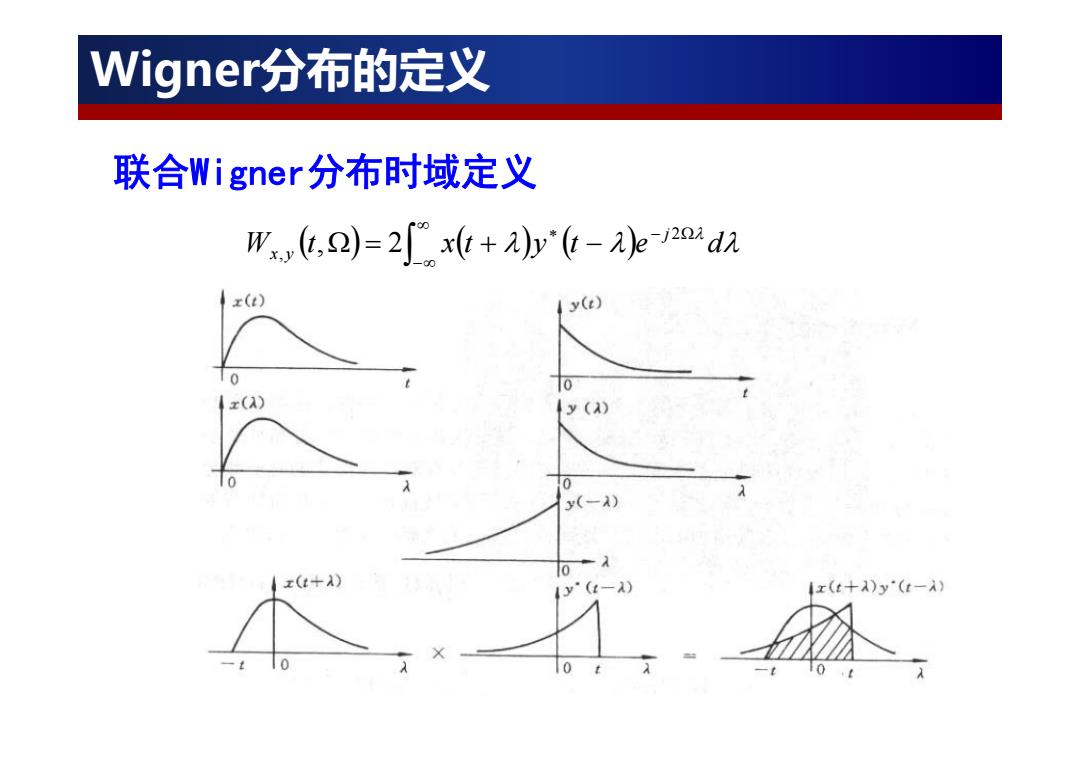
Wigner分布的定义 联合Wigner:分布时域定义 W.,(t)=2"x(t+A)y"(-A)e-12oida x(t) y(t) y(A) 0 y(-A) x(+A) 1y(t-) x(t+)y'(t-)
W t x t y t e d j x y 2 , , 2 联合Wigner分布时域定义 Wigner分布的定义

Wigners分布的定义 联合Wigner:分布时域定义 信号是由过去某一时间的信号乘以未来某一时间的信号, 所取信号的过去时间相等,为了确定Wigner分布在时间t的 特性,只需将此时刻信号左边部分折叠到右边部分,看是否 有任何重叠。如果有重叠,则在时间t的那些特性就会出现 。也就是说,信号在某时刻是否具备某种特性,只要看该时 刻左右两边这种特性是否有重叠即可
信号是由过去某一时间的信号乘以未来某一时间的信号, 所取信号的过去时间相等,为了确定Wigner分布在时间 t 的 特性,只需将此时刻信号左边部分折叠到右边部分,看是否 有任何重叠 。如果有重叠,则在时间 t的那些特性就会出现 。也就是说,信号在某时刻是否具备某种特性,只要看该时 刻左右两边这种特性是否有重叠即可。 联合Wigner分布时域定义 Wigner分布的定义

Vigner分布的定义 联合Wigner:分布时域定义 令x()=x(t+/2)y()=y(-/2) X(2)=2e2X(22) Y(2)=2e2Y*(22) 则式(3.1.1)可变为: W.,(t,Q)=x()y()edr=X(2)*Y(2) -Jx(2a)y(2-2a)eWi0da
令 , 则式(3.1.1)可变为: x xt 1 2 y yt 1 2 , 11 1 1 4 2 , 4 2 22 2 j x y j t Wt x y e d X Y XY e d 2 1 2 * 1 2 2 2 2 j t j t X eX Y eY 联合Wigner分布时域定义 Wigner分布的定义

Vigner分布的定义 联合Wigner:分布时域定义 )Jx(2)(2-2a)da 令2a=2+0/2,则上式变为 形,(6,2)=2∫X(2+8/2)y(Q-2)emdB(3.1.4) 对自WVD,有 所.k-2元」xQ+0/2)X(Q-02))ed031.5) 显然,D在时域和频域有非常明显的对称形式
令 ,则上式变为 (3.1.4) 对自WVD,有 (3.1.5) 显然,WVD在时域和频域有非常明显的对称形式。 4 2 , 4 , 2 22 2 j t Wt X Y e d x y 2 2 , 1 , 22 2 j t W t X Y ed x y 1 , 22 2 j t Wt X X ed x 联合Wigner分布时域定义 Wigner分布的定义

Vigner分布的定义 联合Wigner分布时域定义 若令r(t,t)=x(t+/2)y(t-t/2) 则 Wy(1,)=rs.y(t,)e-iodr (3.1.6) 显然这是普通的傅立叶变换式,只不过它依赖于时间。但此 处的r,(,)并不是我们以前定义过的相关函数。在时一频分 析中,我们称”(,t)为瞬时互相关
若令 则 (3.1.6) 显然这是普通的傅立叶变换式,只不过它依赖于时间t。但此 处的 并不是我们以前定义过的相关函数。在时-频分 析中,我们称 为瞬时互相关。 r t xt y t x y, , 22 , , , , j Wt rte d xy xy , , r t x y , , r t x y 联合Wigner分布时域定义 Wigner分布的定义

WVD的性质 奇、偶、虚、实性 不论x(t)是实信号还是复值信号,其自WVD都是和2的实函 数,即 W(t,2)∈R ∀t,∀2 (3.2.1) 若为x(t)实信号,则W(,2)不但是t、2的实函数,还是2 的偶函数,即 W(t,2)=W(t,-2) (3.2.2) 对x(),)的互WVD,W(1,2)不一定是实函数,但具有 如下性质: W(t,2)=Wx(t,2) (3.2.3)
不论 是实信号还是复值信号,其自WVD都是 t和 的实函 数,即 (3.2.1 ) 若为 实信号,则 不但是 t、 的实函数,还是 的偶函数,即 (3.2.2 ) 对 , 的互WVD, 不一定是实函数,但具有 如下性质: (3.2.3) x t (, ) Wt R x t, Wt Wt x x , , x t W t x , x t y t W t x y, , Wt Wt xy yx , , , , 奇、偶、虚、实性 WVD的性质

WVD的性质 课堂练习 证明:对x(t),y()的互WVD,Wx,y(t,2) 具有如下性质: Ws.x (t,)=W (t,)
课堂练习 证明:对 , 的互WVD, 具有如下性质: x t y t W t x y, , Wt Wt xy yx , , , , WVD的性质