
Electrically Small Antenna Design
Electrically Small Antenna Design

Outline Definition and limitations of electrically small antenna (ESA) —byL.J.CHU Metamaterial-based efficient ESA(Simulation) -by Richard W.Ziolkowski's group Metamaterial-inspired efficient ESA (Application) -by Richard W.Ziolkowski's group Other groups'work
Outline Definition and limitations of electrically small antenna (ESA) ——by L.J.CHU Metamaterial-based efficient ESA (Simulation) ——by Richard W. Ziolkowski’s group Metamaterial-inspired efficient ESA (Application) ——by Richard W. Ziolkowski’s group Other groups’ work

Definition and limitations of ESA
Definition and limitations of ESA

Definition of electrically small antenna Fields of a short,linear electric-current element 1 E= sine e-jkr 7w6 -1 13 kr3 1 Er=-2c080 e-jkr +) 1 2-j Ze Ea=Z。}+1 kr =Re-iX for TM wave kr + IX ”-ky+ER+forTE wave IRI () We often use koa 1 as the standard for ESA
2 0 2 4 3 0 2 2 2 2 2 1 ( ) for TM wave ( ) 1 for TE wave 1 ( ) e e e m m m kr j E kr Z Z R jX H kr k k j E r Z Z R jX H k k r r 3 | | 1 | | ( ) X R kr Definition of electrically small antenna We often use as the standard fo 0 1 k a r ESA Fields of a short, linear electric-current element
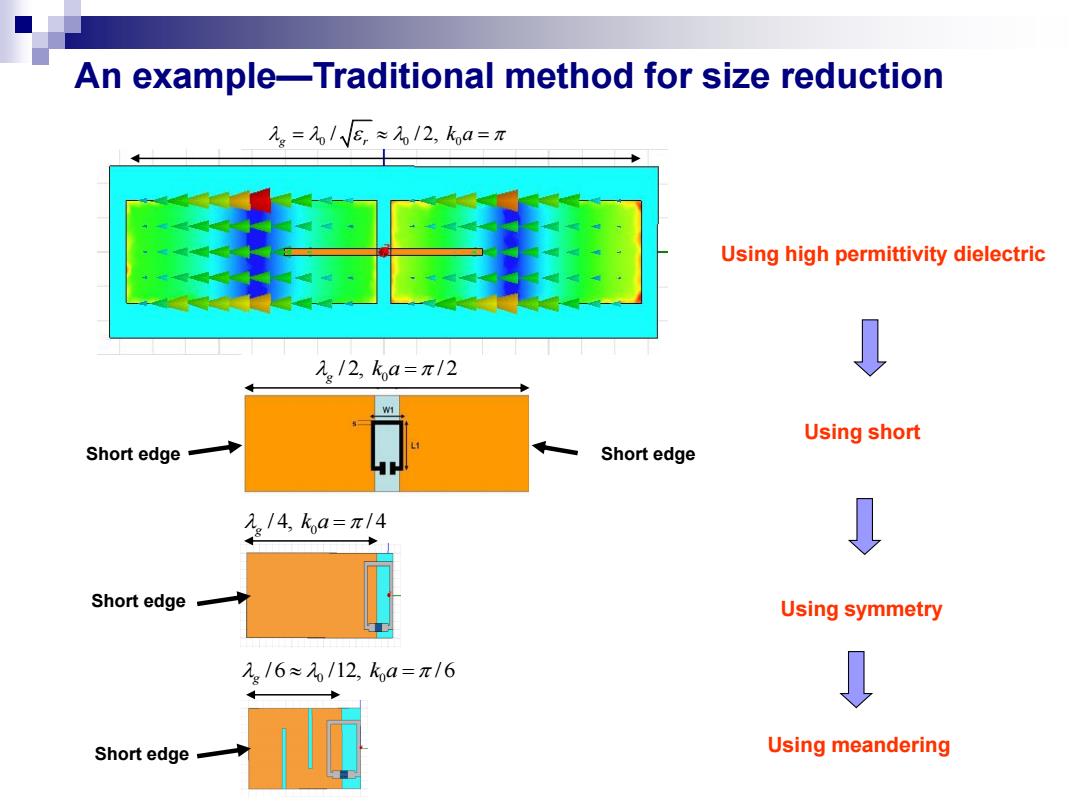
An example-Traditional method for size reduction e=/VB,≈/2,ka=π Using high permittivity dielectric 2。/2,ka=π/2 Using short Short edge Short edge 2./4,ka=π/4 ↓ Short edge Using symmetry 。/6≈/12,ka=π/6 Short edge Using meandering
An example—Traditional method for size reduction Short edge Short edge 0 0 0 / / 2, g r k a 0 / 2, / 2 g k a 0 / 4, / 4 g k a 0 0 / 6 /12, / 6 g k a Using high permittivity dielectric Using short Using symmetry Using meandering Short edge Short edge

Physical limitations of ESA:CHU's limit A.Field of a vertically polarized dipole For the vertically polarized dipole,only TMno waves are required to consider a H=>AnP(cos0)hn(kR), INPUT ANTENNA STRUCTURE B=-() ∑Ar(m+1) hn(kR) XP(cos0)- kR For an arbitrary current distribution =j(月AP.oas and antenna structure,the field out 1 d side the sphere can be expressed in X一-[Rhn(kR)], terms of complete set of orthogonal, kRdR spherical waves P,(cos):Legendre polynomial of order n P(cos):The first associated Legendre polynomial h (kR):spherical Hankel function of second kind L.J.CHU,"Physical limitations of omni-directional antennas",Journal of applied physics,vol.19,Dec 1948
Physical limitations of ESA: CHU’s limit a For an arbitrary current distribution and antenna structure, the field out side the sphere can be expressed in terms of complete set of orthogonal , spherical waves For the vertically polarized dipole, only TMn0 waves are required to consider A. Field of a vertically polarized dipole 1 (cos ) : Legendre polynomial of order n (cos ) : The first associated Legendre polynomial ( ) : spherical Hankel function of second kind n n n P P h kR L.J.CHU, “Physical limitations of omni-directional antennas”, Journal of applied physics, vol.19, Dec 1948

B.Radiation characteristics At a sufficiently large distance from the sphere,the angular distribution of the radiation field is givern by the series of the associated Legendre polynomials E。=(u/e)eR/R H。=(e/4)E *空a-0 n(+1) [P(cos0)]sin0d0=- 2n+11 and 4πE2 G()= inadoie ∫P,1(cos0P4((o)6d0=0 for≠. |∑An(-1)+/P1(cos0)12 21A n(n+1) 2n+1
B. Radiation characteristics At a sufficiently large distance from the sphere, the angular distribution of the radiation field is givern by the series of the associated Legendre polynomials
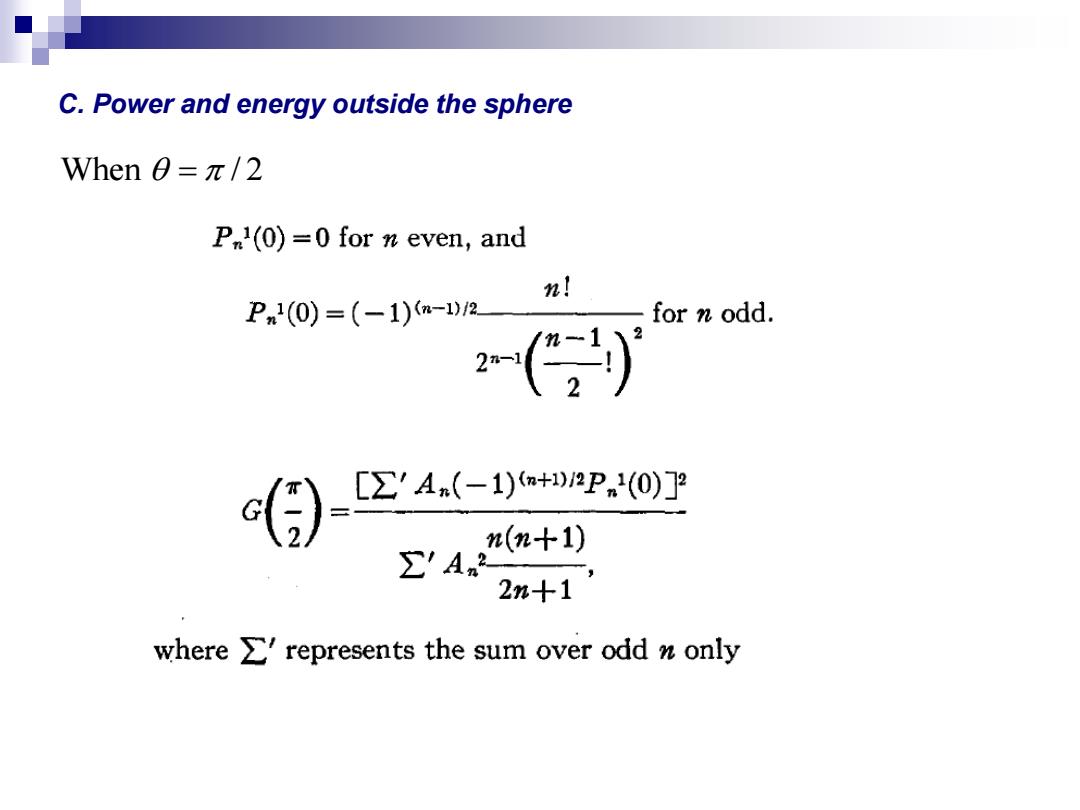
C.Power and energy outside the sphere When0=π/2 P1(0)=0 for n even,and Pm2(0)=(-1)m-1w2 for n odd. 2-(2)》 [∑'A(-1)m+2Pn1(0)]2 (m+1) ∑'An2 2n+1 where >represents the sum over odd n only
When / 2 C. Power and energy outside the sphere

Total complex power at the surface of the sphere P(a)-" ×H'asinθdOdφ e()f 1h (cha) where d p=ka,hin=hn(p),(phn)'=phn(p). do The average radiated power is the real part =(月) 2n+1 But the stored power is not the imaginary part.The imaginary part just equals to the difference of electric energy and magnetic energy
Total complex power at the surface of the sphere The average radiated power is the real part 2 * 2 0 0 P a E H a d d ( ) sin But the stored power is not the imaginary part. The imaginary part just equals to the difference of electric energy and magnetic energy
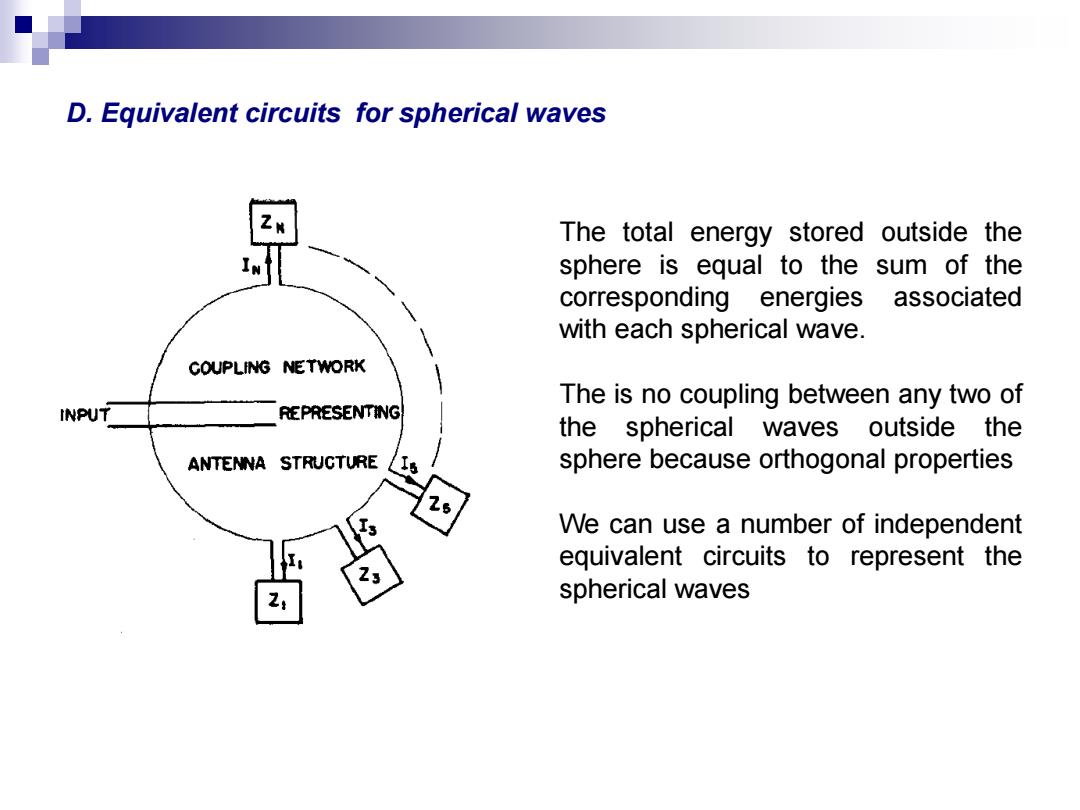
D.Equivalent circuits for spherical waves The total energy stored outside the sphere is equal to the sum of the corresponding energies associated with each spherical wave. COUPLING NETWORK The is no coupling between any two of INPUT REPRESENTING the spherical waves outside the ANTENNA STRUCTURE sphere because orthogonal properties 26 We can use a number of independent equivalent circuits to represent the 2 spherical waves
The total energy stored outside the sphere is equal to the sum of the corresponding energies associated with each spherical wave. The is no coupling between any two of the spherical waves outside the sphere because orthogonal properties We can use a number of independent equivalent circuits to represent the spherical waves D. Equivalent circuits for spherical waves