
信号处理理论与算法 随机信号分析 张朋 自动化工程学院 1
1 信号处理理论与算法 随机信号分析 张 朋 自动化工程学院

随机信号的相关和功率谱分析 一、随机信号基本概念 二、信号的幅值域分析 三、相关分析及其应用 四、功率谱分析及其应用 3
3 随机信号的相关和功率谱分析 一、随机信号基本概念 二、信号的幅值域分析 三、相关分析及其应用 四、功率谱分析及其应用
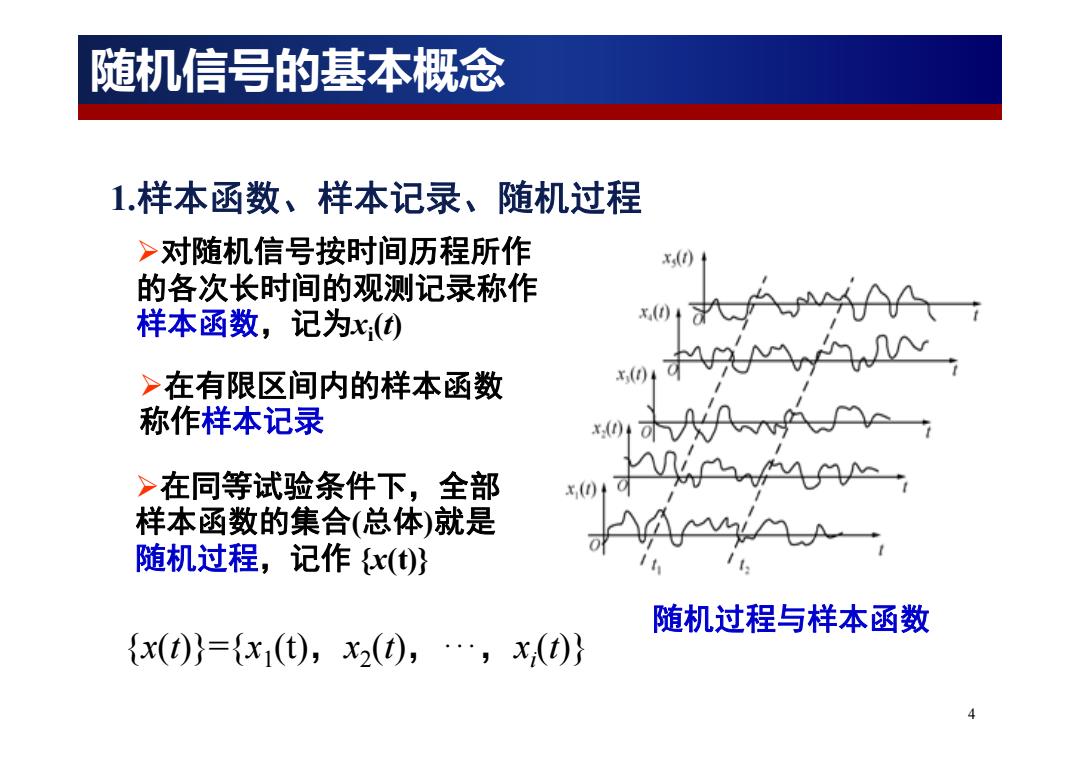
随机信号的基本概念 1.样本函数、样本记录、随机过程 >对随机信号按时间历程所作 的各次长时间的观测记录称作 样本函数,记为() >在有限区间内的样本函数 称作样本记录 x() >在同等试验条件下,全部 (t) 样本函数的集合(总体)就是 随机过程,记作{x()} 随机过程与样本函数 {x()}={x1(),x2(t),…,x,(t)} 4
4 1.样本函数、样本记录、随机过程 随机过程与样本函数 对随机信号按时间历程所作 的各次长时间的观测记录称作 样本函数,记为xi(t) 在同等试验条件下,全部 样本函数的集合(总体)就是 随机过程,记作 {x(t)} 在有限区间内的样本函数 称作样本记录 {x(t)}={x1(t),x2(t),ꞏꞏꞏ,xi(t)} 随机信号的基本概念
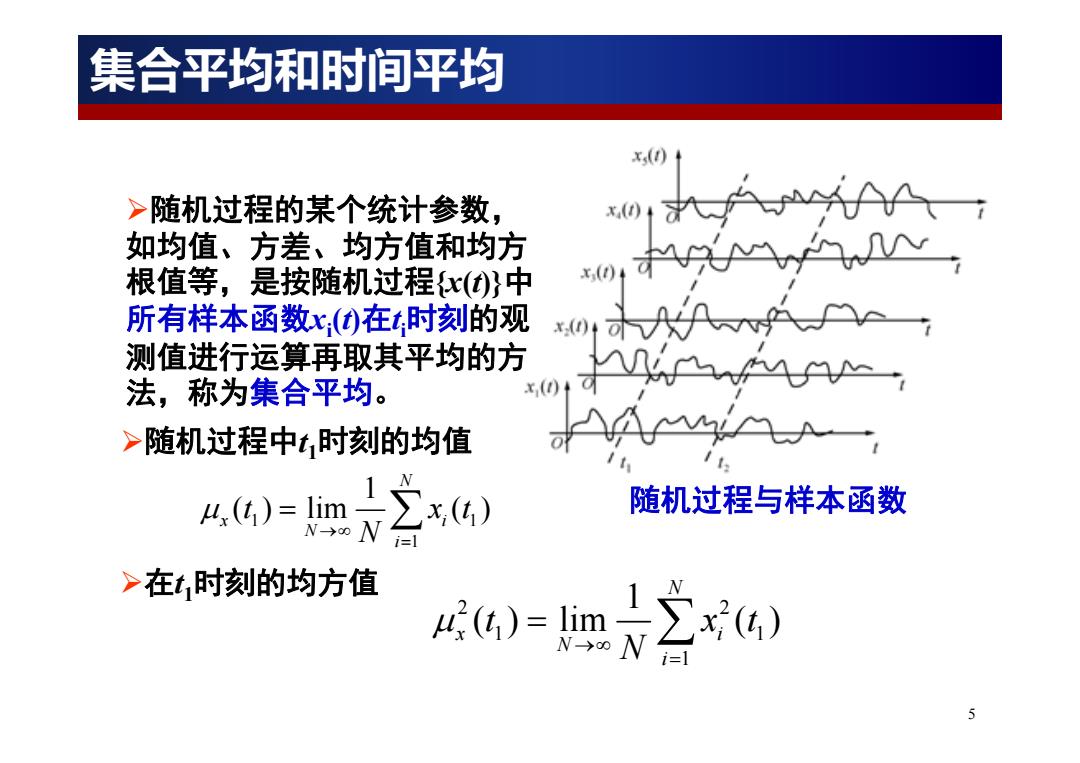
集合平均和时间平均 >随机过程的某个统计参数, 如均值、方差、均方值和均方 根值等,是按随机过程x()}中 x(1 所有样本函数()在t时刻的观 x(0 测值进行运算再取其平均的方 法,称为集合平均。 >随机过程中t,时刻的均值 )=m立) 随机过程与样本函数 >在t时刻的均方值 c)-m立c) 5
5 随机过程与样本函数 随机过程的某个统计参数, 如均值、方差、均方值和均方 根值等,是按随机过程{x(t)}中 所有样本函数xi(t)在ti时刻的观 测值进行运算再取其平均的方 法,称为集合平均。 1 1 1 1 ( ) lim ( ) N x i N i t xt N 随机过程中t1时刻的均值 在t1时刻的均方值 2 2 1 1 1 1 ( ) lim ( ) N x i N i t xt N 集合平均和时间平均
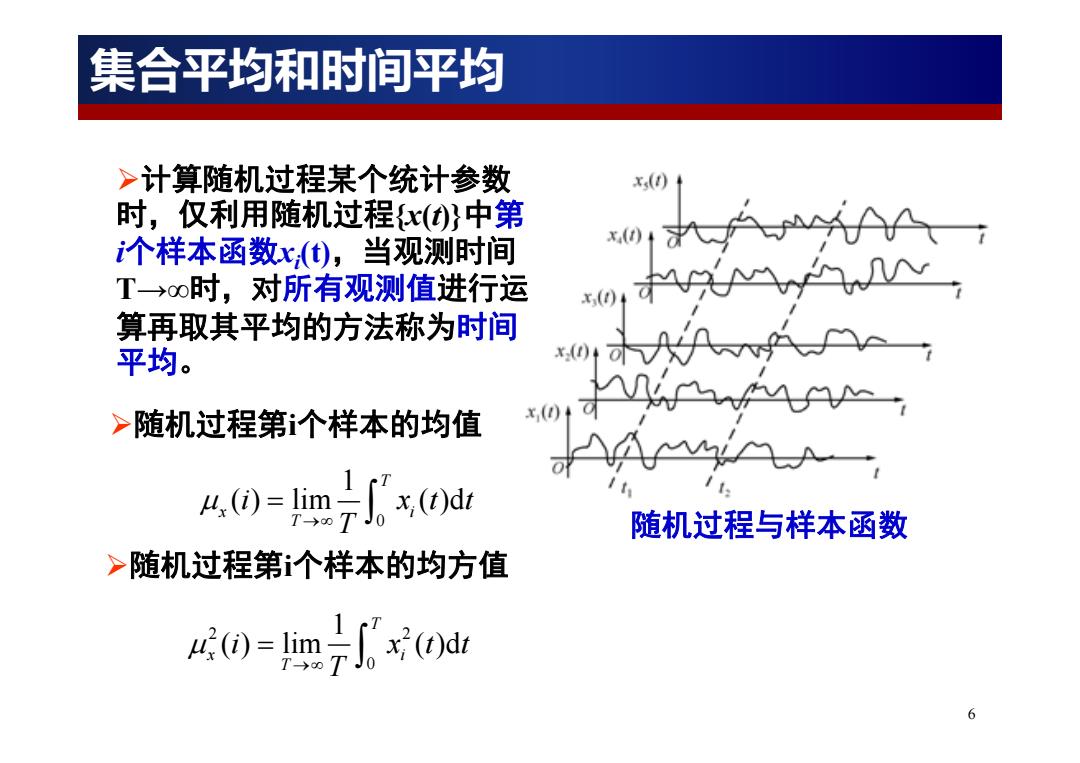
集合平均和时间平均 >计算随机过程某个统计参数 x() 时,仅利用随机过程x()}中第 个样本函数x,),当观测时间 T→0时,对所有观测值进行运 x() 算再取其平均的方法称为时间 平均。 x() >随机过程第个样本的均值 40=m子Jxr 随机过程与样本函数 >随机过程第个样本的均方值 (md 6
6 随机过程与样本函数 计算随机过程某个统计参数 时,仅利用随机过程{x(t)}中第 i个样本函数xi(t),当观测时间 T→∞时,对所有观测值进行运 算再取其平均的方法称为时间 平均。 0 1 ( ) lim ( )d T x i T i xt t T 2 2 0 1 ( ) lim ( )d T x i T i xtt T 随机过程第i个样本的均值 随机过程第i个样本的均方值 集合平均和时间平均

随机信号的主要特征参数 >描述各态历经随机过程的主要特征参数有 V均值4,、均方值W、方差o2 描述信号在幅值域中强度方面的特征 √概率密度函数—描述信号在幅值域中的特征; √自相关函数—描述信号在时延域中的特征; √功率谱密度函数一描述信号在频域中的特征 >描述两个或两个以上各态历经随机信号之间的相互依赖程度: √(1)联合概率密度函数; √(2)互相关函数; √(3)互谱密度函数和相关/相干函数。 7
7 描述各态历经随机过程的主要特征参数有 均值 、均方值 、方差 ——描述信号在幅值域中强度方面的特征 概率密度函数——描述信号在幅值域中的特征; 自相关函数——描述信号在时延域中的特征; 功率谱密度函数——描述信号在频域中的特征 x 2 x 2 x 描述两个或两个以上各态历经随机信号之间的相互依赖程度: (1) 联合概率密度函数; (2) 互相关函数; (3) 互谱密度函数和相关/相干函数。 随机信号的主要特征参数
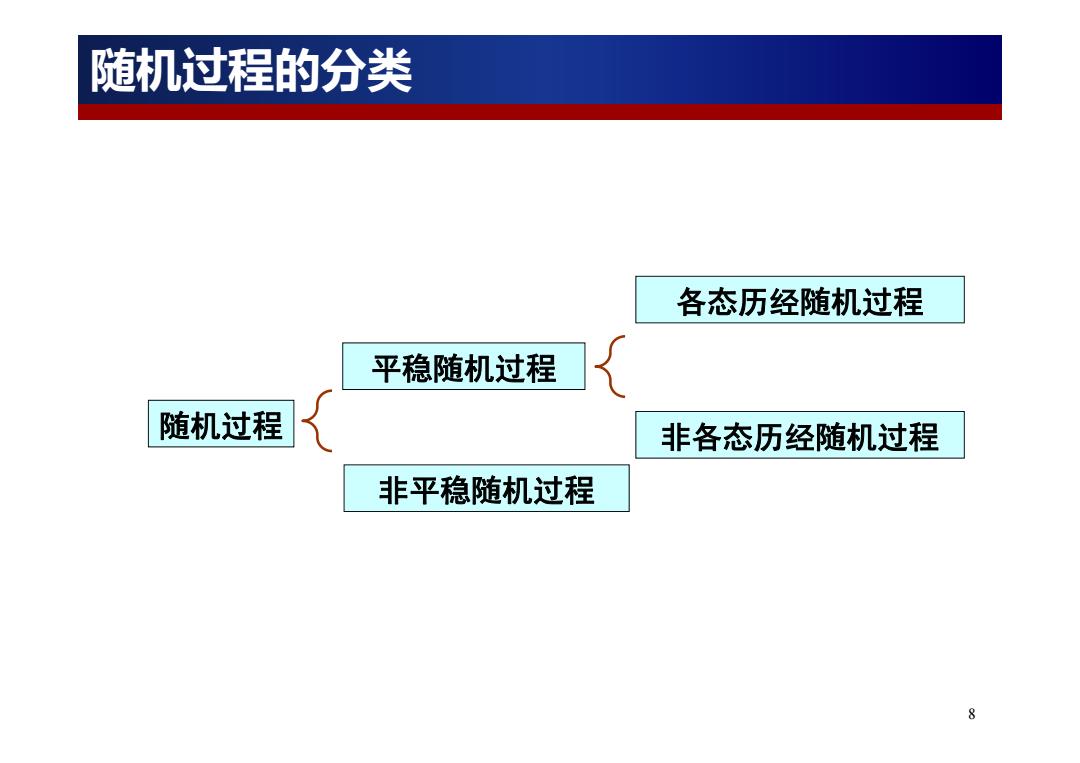
随机过程的分类 各态历经随机过程 平稳随机过程 随机过程 非各态历经随机过程 非平稳随机过程 8
8 平稳随机过程 非平稳随机过程 各态历经随机过程 随机过程 非各态历经随机过程 随机过程的分类

信号的幅值域分析 1.统计特征参数 √均值 √均方值 =mxe √均方根值 (dirv. V方差 g=mI0-4rd山l 均值、方差和均方值之间的关系σ=少一从 9
9 1. 统计特征参数 均值 0 1 lim ( )d T x T x t t T 均方值 均方根值 方差 2 2 0 1 lim ( )d T x T x t t T 2 rms 0 1 lim ( )d T x T x xtt T 2 2 0 1 lim ( ) d T x x T xt t T 2 22 均值、方差和均方值之间的关系 x xx 信号的幅值域分析
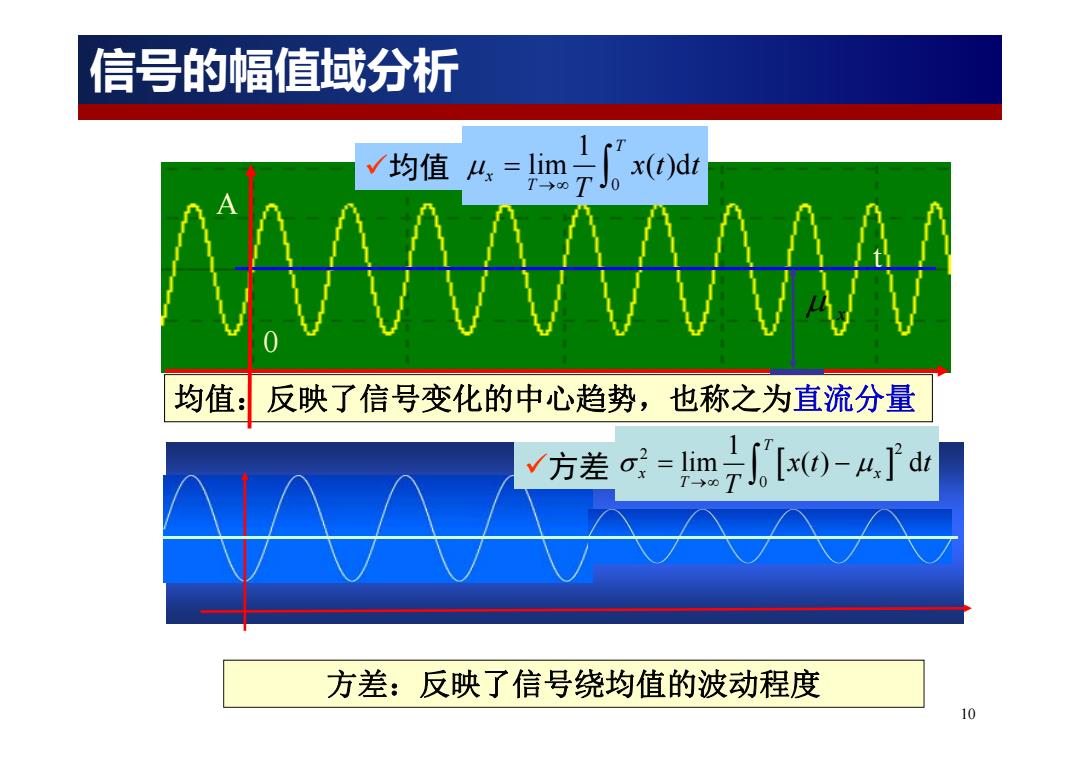
信号的幅值域分析 v均值么=钾x0u 均值: 反映了信号变化的中心趋势,也称之为直流分量 方差=m[0-4,d山 方差:反映了信号绕均值的波动程度 10
10 A 0 t 均值:反映了信号变化的中心趋势,也称之为直流分量 x 均值 0 1 lim ( )d T x T x t t T 方差:反映了信号绕均值的波动程度 方差 2 2 0 1 lim ( ) d T x x T xt t T 信号的幅值域分析

均值、均方值和方差的估计 √均值 a.=0 √均方值 -ro灿 =m7xo灿 √方差 &-HfIx-4J 云=m7[0-4'd业 11
11 均值 0 1 lim ( )d T x T x t t T 均方值 方差 2 2 0 1 lim ( )d T x T x t t T 2 2 0 1 lim ( ) d T x x T xt t T 0 1 ( )d T x xt t T 2 2 0 1 () d T x x x t t T 2 2 0 1 ( )d T x x t t T 均值、均方值和方差的估计