
信号处理理论与算法 非参数功率谱估计 张朋 自动化工程学院 1
信号处理理论与算法 非参数功率谱估计 张 朋 自动化工程学院 1

基本概念 谱估计定义: 利用有限的样本数据估计一个平稳随机 信号的功率谱密度。 从观察样本估计信号的功率分布情况。 应用: 寻找数据的“隐周期性” 信号频谱分析 基于DFT功率谱估计 2
谱估计定义: 利用有限的样本数据估计一个平稳随机 信号的功率谱密度。 从观察样本估计信号的功率分布情况。 应用: 寻找数据的“隐周期性” 信号频谱分析 基于DFT功率谱估计 基本概念 2

功率谱估计的应用 1.雷达回波信号处理: 功率谱密度值的宽度:运动目标的位置 功率谱密度峰值的高度:运动目标的强度 功率谱密度峰值的位置:运动目标的速度 2.无源声纳信号处理 功率谱密度位置:目标的方向 3.语音处理 基音提取 估计声音语调共振峰 基于谱减法的语音增强算法 4.生物工程领域 功率谱密度的峰形和波形:癫痫病的发作周期 3
1.雷达回波信号处理: 功率谱密度值的宽度:运动目标的位置 功率谱密度峰值的高度:运动目标的强度 功率谱密度峰值的位置:运动目标的速度 2.无源声纳信号处理 功率谱密度位置:目标的方向 3.语音处理 基音提取 估计声音语调共振峰 基于谱减法的语音增强算法 4.生物工程领域 功率谱密度的峰形和波形:癫痫病的发作周期 功率谱估计的应用 3
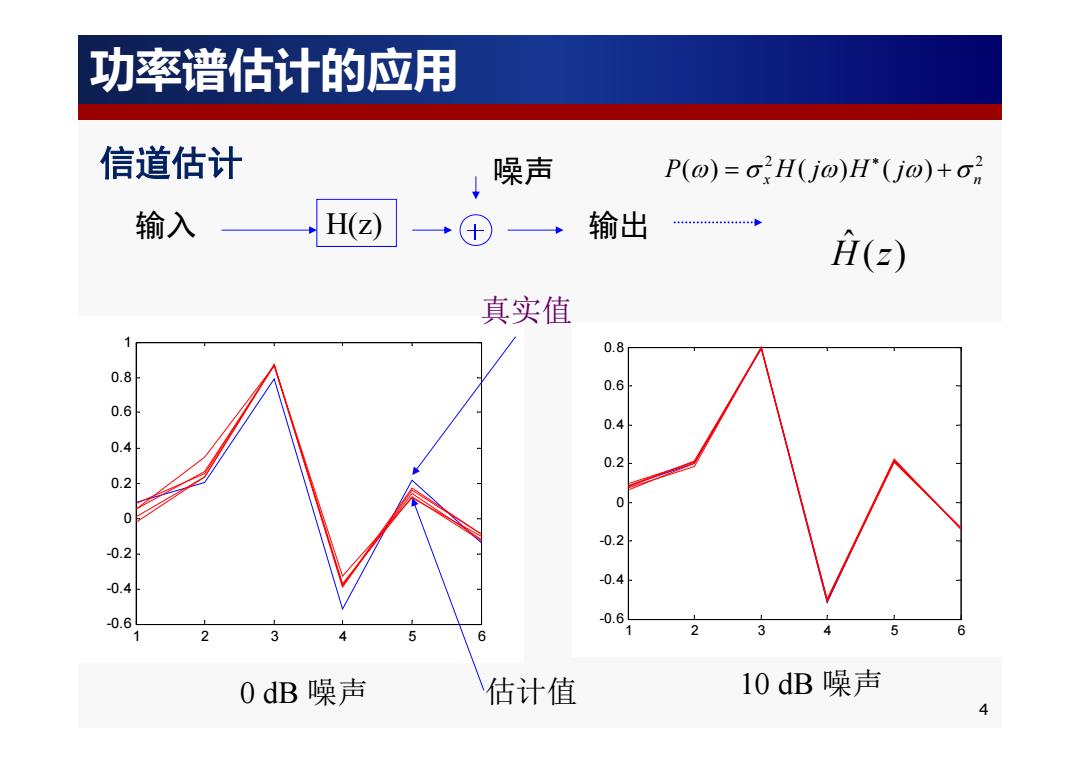
功率谱估计的应用 信道估计 噪声 P(@)=o2H(j@)H'(j@)+o2 输入 H(z) 输出 44444444444 H(e) 真实值 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 -0.2 -0.2 -0.4 -0.4 -0.6 -0.6 2 3 1 5 6 3 3 5 6 0dB噪声 估计值 10dB噪声 4
信道估计 1 2 3 4 5 6 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1 2 3 4 5 6 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 输入 H(z) 输出 噪声 ( ) ˆ H z 真实值 0 dB 噪声 估计值 10 dB 噪声 2 2 () ( ) ( ) P Hj H j x n 功率谱估计的应用 4
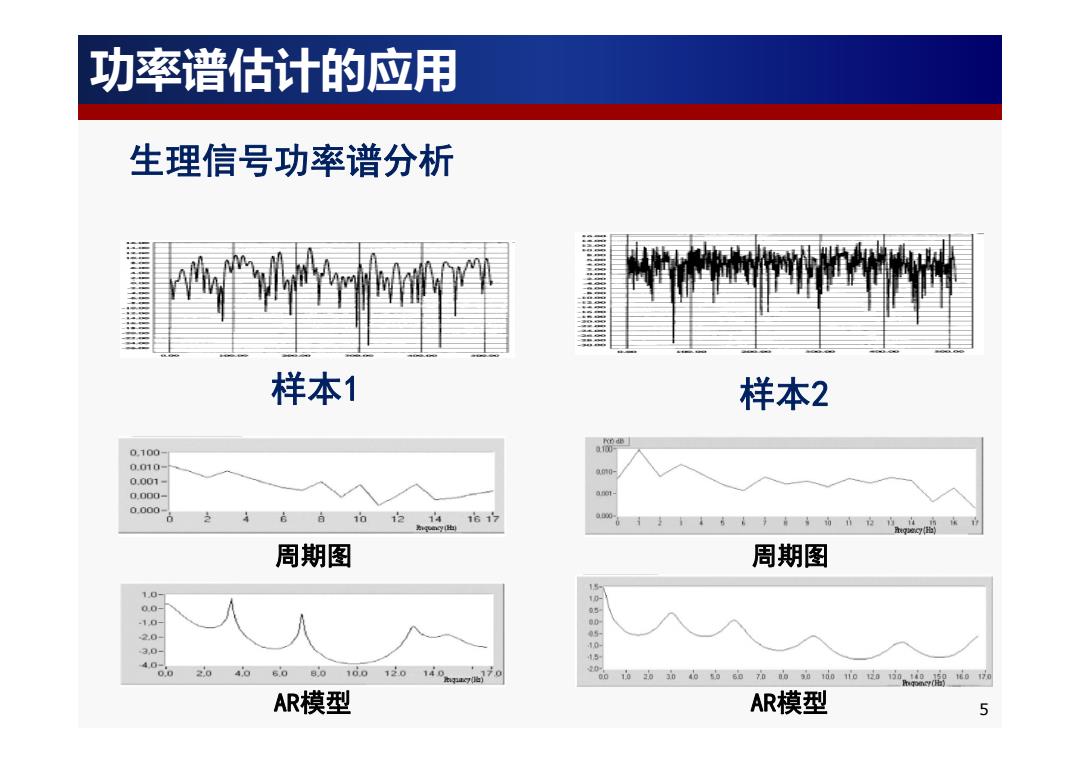
功率谱估计的应用 生理信号功率谱分析 样本1 样本2 0.100 0.0m0 0.001 0.000 0.000 24 67 .00- 周期图 周期图 10 00 10 20 30- 40 0.0 40 AR模型 AR模型 5
生理信号功率谱分析 功率谱估计的应用 周期图 AR模型 样本2 周期图 AR模型 样本1 5
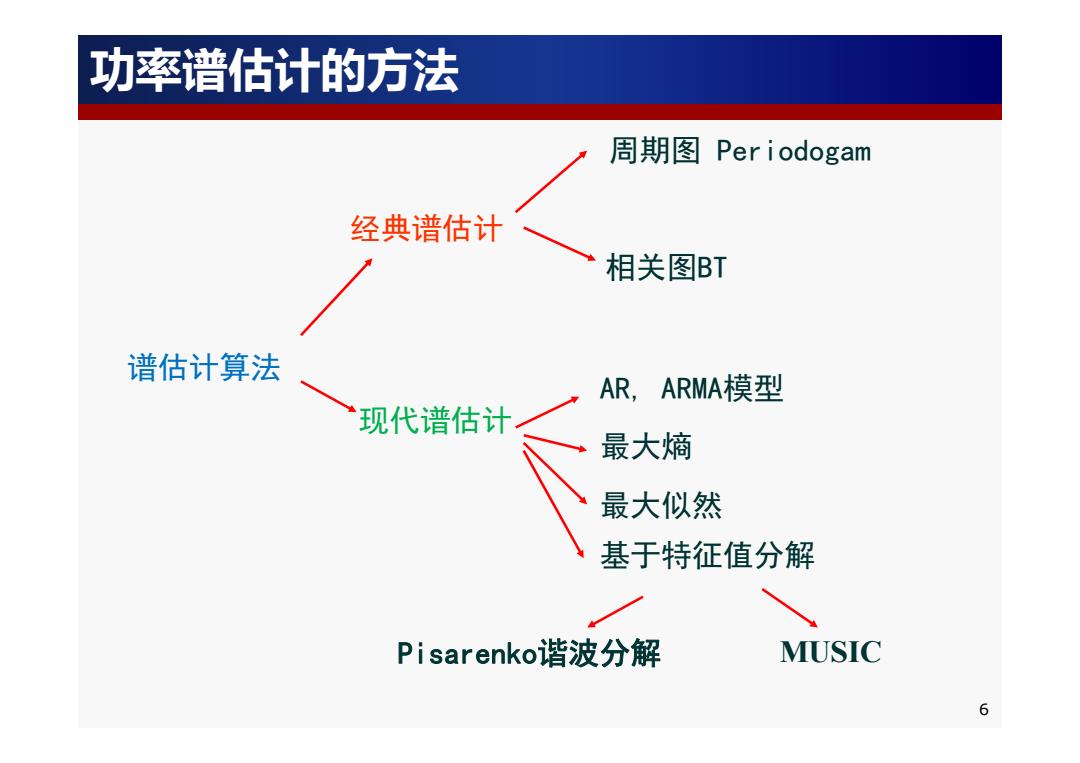
功率谱估计的方法 周期图Per iodogam 经典谱估计 相关图BT 谱估计算法 AR,ARMA模型 现代谱估计 最大熵 最大似然 基于特征值分解 Pi sarenkoi谐波分解 MUSIC 6
谱估计算法 现代谱估计 经典谱估计 周期图 Periodogam 相关图BT AR, ARMA模型 最大熵 最大似然 基于特征值分解 Pisarenko谐波分解 MUSIC 功率谱估计的方法 6

非参数谱估计的理论基础 估计的主要研究内容 (1)估计子0是如何接近真实参数0的?("接近度"评价) (2)参数估计方法 估计的定义 己知N个数据x,…,xw估计真实参数0,…,O, 即N维样本空间映射→p维参数空间,Xv→0(p维) 小样本性能(W个数据得到的估计子性能):计算机仿真 大样本性能(渐近性能,N→∞):理论分析 7
估计的定义 1 1 ,, ,, , ( ) ( ,) N p N N xx Np p N N 映射 已知 个数据 估计真实参数 即 维样本空间 维参数空间 ( 维) 小样本性能 个数据得到的估计子性能 :计算机仿真 大样本性能 渐近性能 :理论分析 ^ (1)估计子 是如何接近真实参数 的?("接近度"评价) N (2)参数估计方法 估计的主要研究内容 非参数谱估计的理论基础 7

非参数谱估计的理论基础 x(n)的自相关函数R(k)=E{x(n+k)x(m)} 两种估计: -之a6ia 因=之a6rm (具有相关函数矩阵的"半正定性") 两种估计的性能: EiR(k)=R.(x) 无偏估计 (K)-NkR() 有偏估计(渐近无偏估计) N 渐近无偏估计: lim E}=0 N 无偏估计一定是渐近无偏估计,反之一般不成立 “好”的估计:应该是渐近无偏估计 8
1 2 N ˆ { ( )} ( ) ˆ { ( )} ( ) ( ) ˆ : lim { } x x N ER k R x N k ER k R x N E 两种估计的性能: 无偏估计 有偏估计 渐近无偏估计 渐近无偏估计 无偏估计一定是渐近无偏估计,反之一般不成立 “好”的估计:应该是渐近无偏估计 * * 1 1 * 2 1 ( ) ( ) { ( ) ( )} : 1 ˆ ( ) ( ) ( ) 1 ˆ ( ) ( ) ( ) ( " ") x N k n N k n xn R k Exn kx n R k xn kx n N k R k xn kx n N 的自相关函数 两种估计 具有相关函数矩阵的 半正定性 非参数谱估计的理论基础 8

非参数谱估计的理论基础 两个无偏估计(或其中一个渐进无偏估计)的性能比较: 估计方差:Var(0)=E{[Ow-E(0w]} 均方误差:MP(0N)=E{[ON-0]2}=E{[Ow-E(0w)+E(ON)-8]'} =E[Ox-E(ON))+E[E(ON)-0]2)+2E([ON-E(Ox)][E(ON)-0]) =Var(0w)+b2(0w) 无偏估计的评价:若Var(01)<Var(02),则称01比O2好 有偏估计的评价:若M2(01)<M2(02),则称01优于02 注:比较估计子性能时,用均方误差比只用方差或偏差更合理 9
两个无偏估计(或其中一个渐进无偏估计)的性能比较: ^ ^ 2 ^ ^ ^^ ^ 22 2 ^^ ^ ^^ ^ 2 2 ^ ^ 2 ^ ^ ^^ 1 2 12 ˆ : ( ) {[ ( )] } : ( ) {[ ] } {[ ( ) ( ) ] } {[ ( )] } {[ ( ) ] } 2 {[ ( )][ ( ) ]} () () ( ) ( ), N N N N N NN N NN N NN N N N Var E E M E EEE E E EE E E E Var b Var Var 估计方差 均方误差 无偏估计的评价:若 则称 比 好 有偏 ^ ^ ^^ 2 2 ( ) ( ), 1 2 12 : 估计的评价:若 则称 优于 M M 注 比较估计子性能时,用均方误差比只用方差或偏差更合理 非参数谱估计的理论基础 9

非参数谱估计的理论基础 评价参数估计好坏的问题: ~采用均方误差来衡量参数估计的优劣 - 判断无偏估计是否最好:使用费舍尔(Fisher).信息,满 足克拉美罗(Cramer-Rao)下界 如何进行参数估计: Bayes估计(关键选什么风险函数) 最大似然估计(需知道似然函数形式) -线性均方估计(正交性原理) 最小二乘估计(若é零均值、同方差,则最小二乘法是 最优的,否则要用加权最小二乘法) 10
评价参数估计好坏的问题: –采用均方误差来衡量参数估计的优劣 –判断无偏估计是否最好:使用费舍尔(Fisher)信息,满 足克拉美罗(Cramer-Rao)下界 如何进行参数估计: –Bayes估计(关键选什么风险函数) –最大似然估计(需知道似然函数形式) –线性均方估计(正交性原理) –最小二乘估计(若e零均值、同方差,则最小二乘法是 最优的,否则要用加权最小二乘法) 非参数谱估计的理论基础 10