
第3讲图论
第3讲 图论
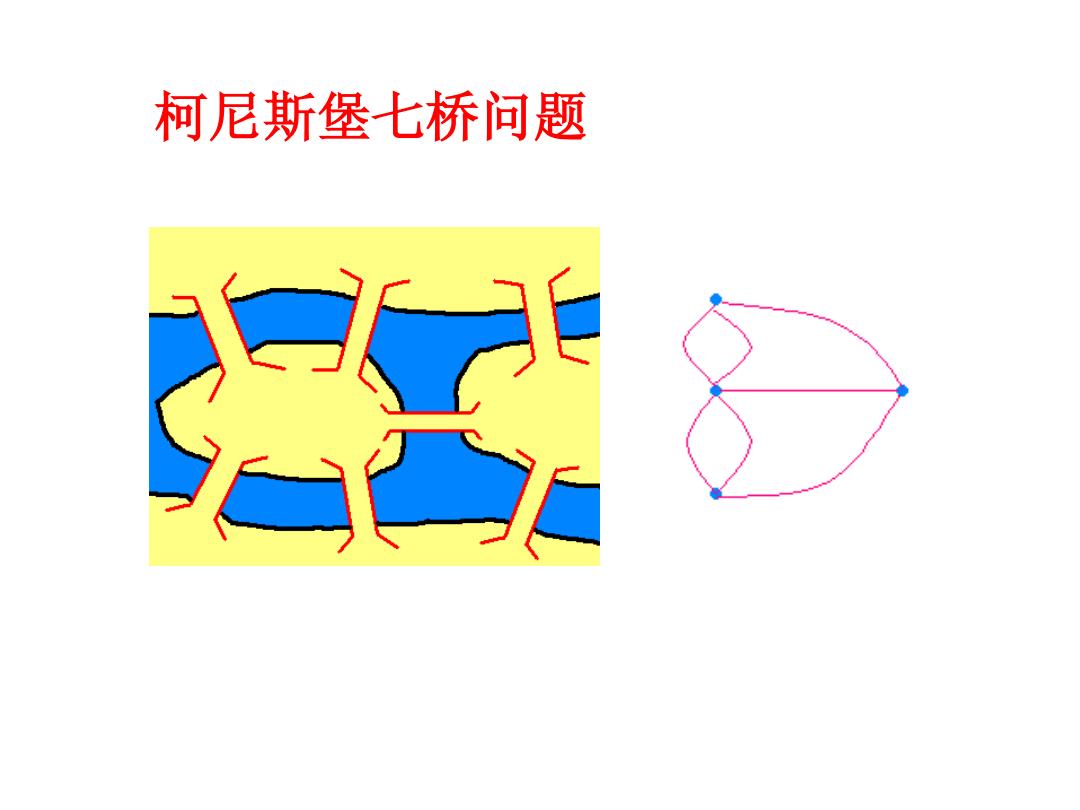
柯尼斯堡七桥问题
柯尼斯堡七桥问题

莱昂哈德~欧拉(Leonhard Euler, 1707年4月5日~1783年9月18日)是 瑞士数学家和物理学家。他被一些数学 史学者称为历史上最伟大的两位数学家 之一。欧拉是第一个使用“函数”一词 来描述包含各种参数的表达式的人,例 如:y=F(x)(函数的定义由莱布尼兹 在1694年给出)。他是把微积分应用于 物理学的先驱者之一。 柯尼斯堡七桥: 在1736年(29岁),欧拉解决了柯尼斯堡七桥问题,并且发 表了论文《关于位置几何问题的解法》,对一笔画问题进行了阐 述,是最早运用图论和拓扑学的典范
柯尼斯堡七桥: 在1736年(29岁),欧拉解决了柯尼斯堡七桥问题,并且发 表了论文《关于位置几何问题的解法》,对一笔画问题进行了阐 述,是最早运用图论和拓扑学的典范。 莱昂哈德·欧拉(Leonhard Euler , 1707年4月5日~1783年9月18日)是 瑞士数学家和物理学家。他被一些数学 史学者称为历史上最伟大的两位数学家 之一。欧拉是第一个使用“函数”一词 来描述包含各种参数的表达式的人,例 如:y = F(x) (函数的定义由莱布尼兹 在1694年给出)。他是把微积分应用于 物理学的先驱者之一
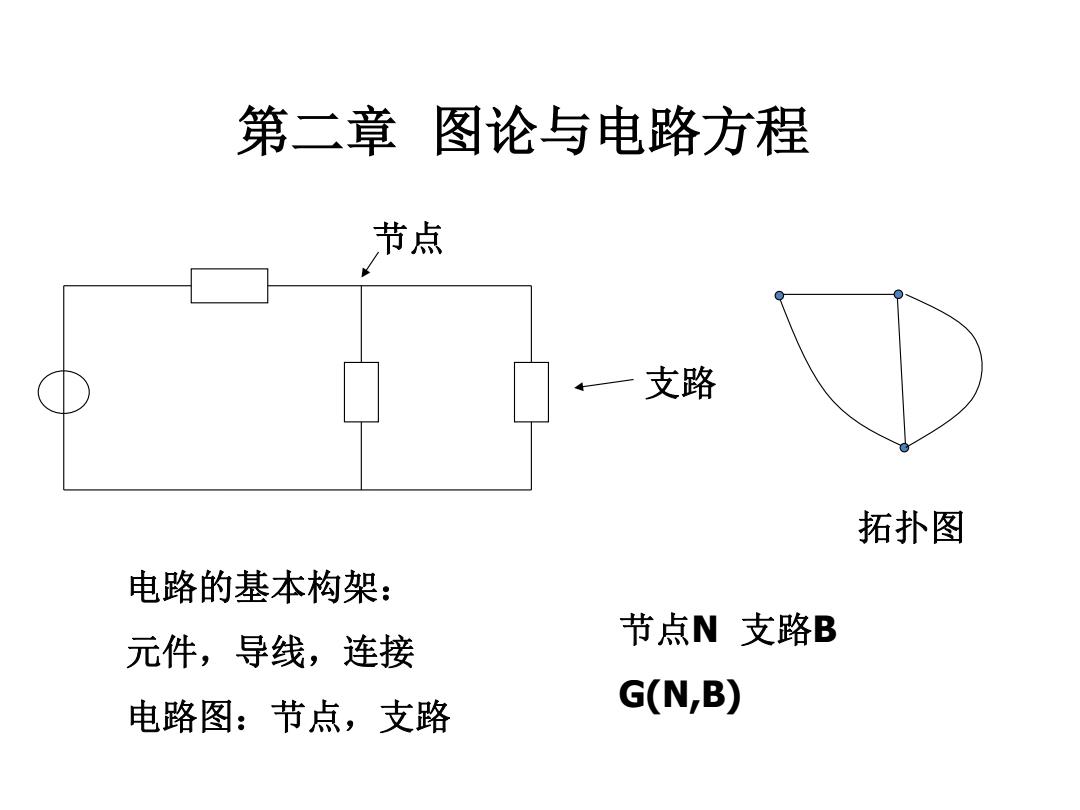
第二章图论与电路方程 节点 支路 拓扑图 电路的基本构架: 元件,导线,连接 节点N支路B 电路图:节点,支路 G(N,B)
第二章 图论与电路方程 电路的基本构架: 元件,导线,连接 电路图:节点,支路 节点N 支路B G(N,B) 节点 支路 拓扑图
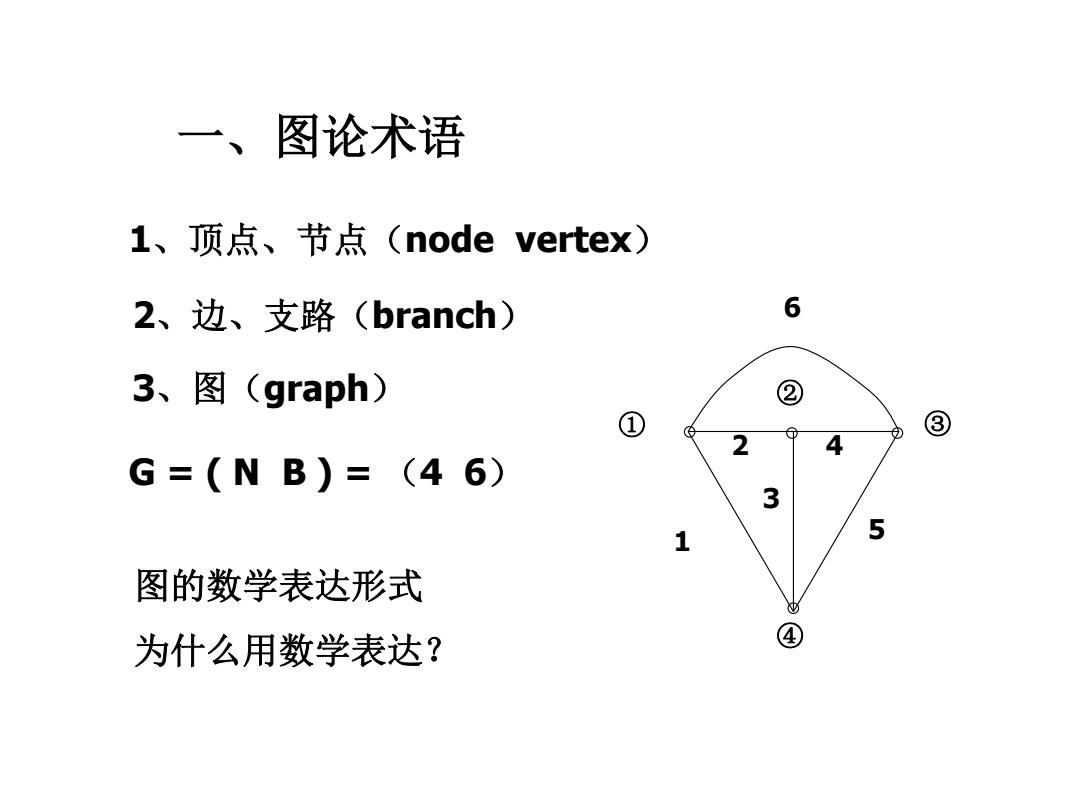
一、图论术语 i、J顶点、节点(node vertex) 2、边、支路(branch) 6 3、图(graph) ② ① ③ 2 4 G=(NB)=(46) 3 1 5 图的数学表达形式 为什么用数学表达? ④
一、图论术语 1、顶点、节点(node vertex) 2、边、支路(branch) 3、图(graph) G = ( N B ) = (4 6) ① ② ③ ④ 1 2 3 4 5 6 图的数学表达形式 为什么用数学表达?
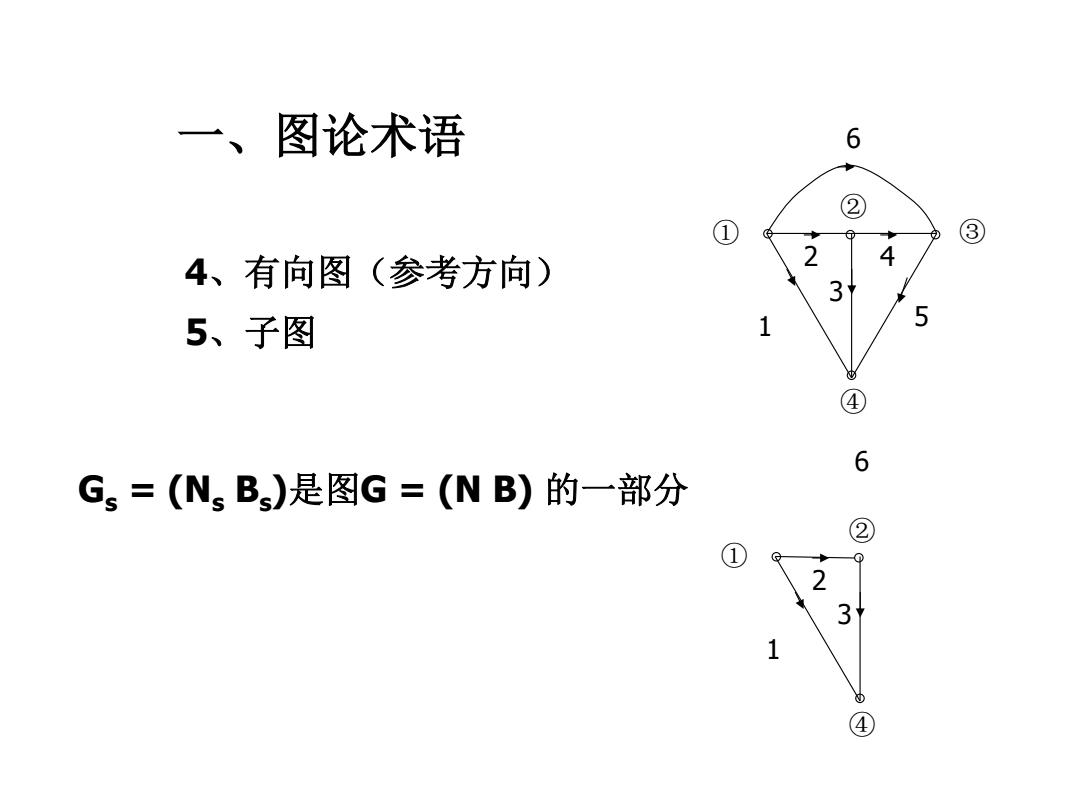
一、图论术语 6 ② ① ③ 4 4、有向图(参考方向) 2 3 5、子图 1 5 ④ 6 Gs=(NBs)是图G=(NB)的一部分 ② ① 2 3》 1 ④
一、图论术语 4、有向图(参考方向) ① ② ③ ④ 1 2 3 4 5 6 5、子图 Gs = (Ns Bs )是图G = (N B) 的一部分 ① ② ④ 1 2 3 6
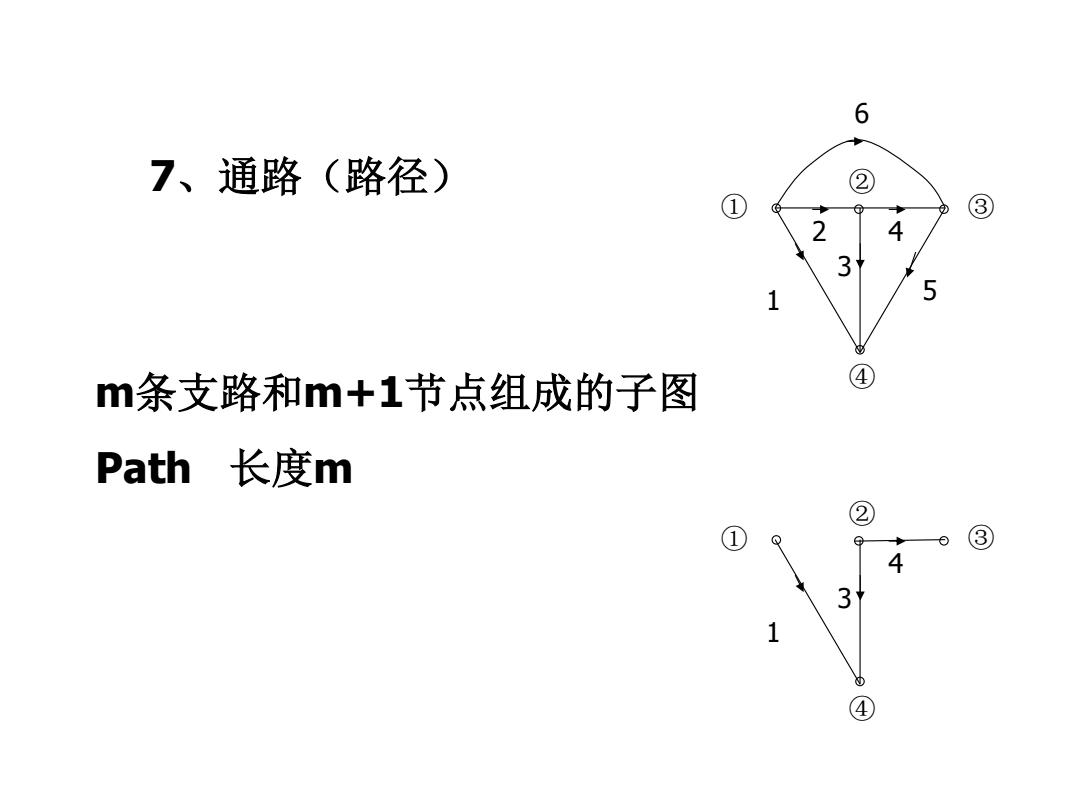
6 7、通路(路径) ② ① ③ 4 3 1 5 m条支路和m+1节点组成的子图 ④ Path长度m ② ① ③ 4 31 1 ④
7、通路(路径) m条支路和m+1节点组成的子图 Path 长度m ① ② ③ ④ 1 2 3 4 5 6 ① ③ ④ 1 3 4 ②
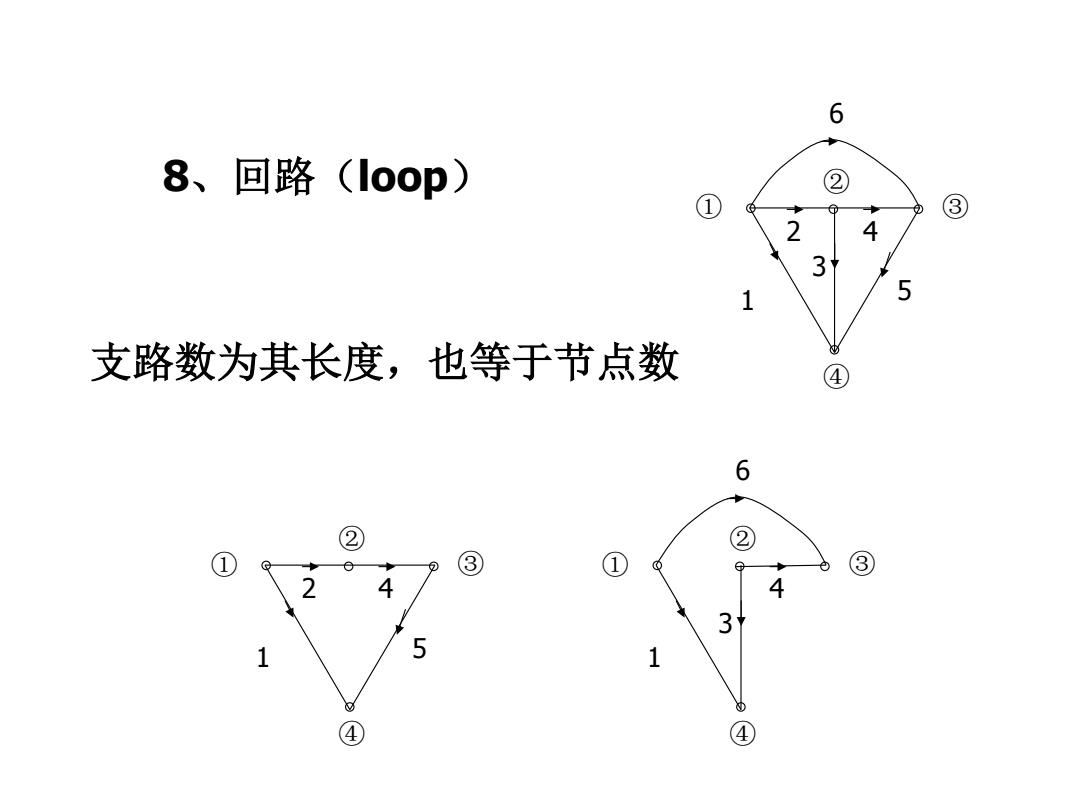
6 8、回路(Ioop) ② ③ 2 4 3 1 5 支路数为其长度,也等于节点数 ④ 6 ② 2 ③ ① ③ 4 4 1 5 1 ④ ④
8、回路(loop) 支路数为其长度,也等于节点数 ① ② ③ ④ 1 2 3 4 5 6 ① ② ③ ④ 1 2 4 5 ① ② ③ ④ 1 3 4 6
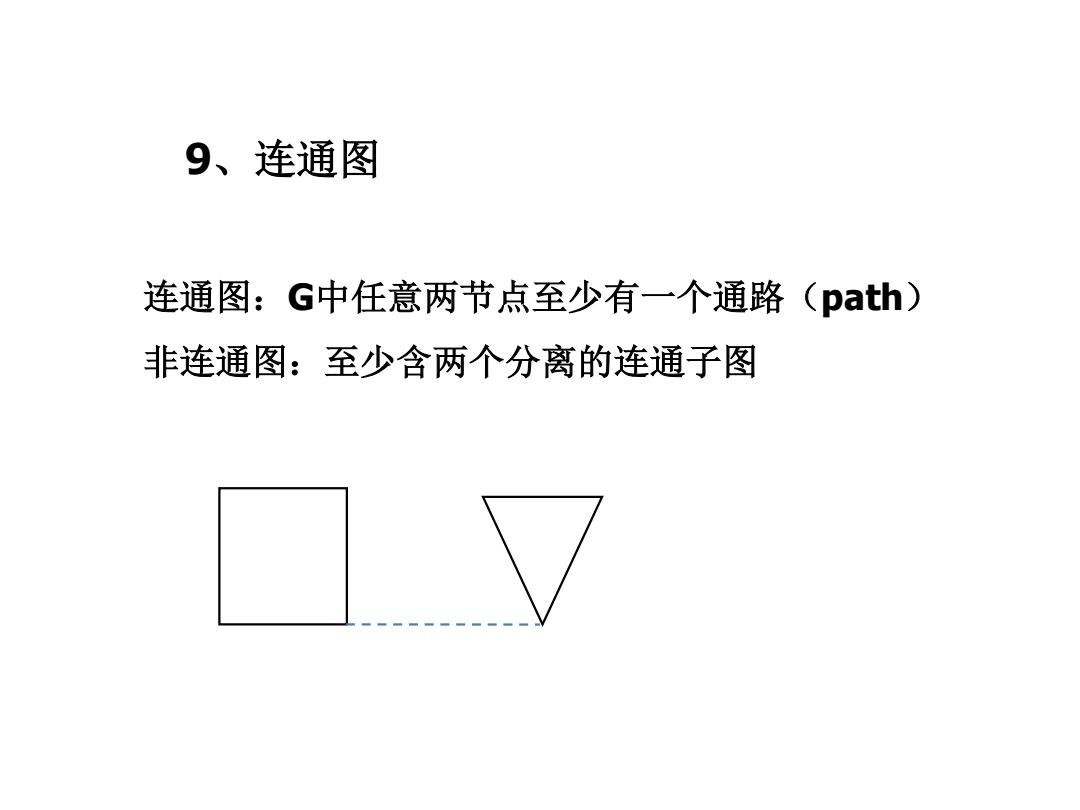
9、连通图 连通图:G中任意两节点至少有一个通路(path) 非连通图:至少含两个分离的连通子图
9、连通图 连通图:G中任意两节点至少有一个通路(path) 非连通图:至少含两个分离的连通子图
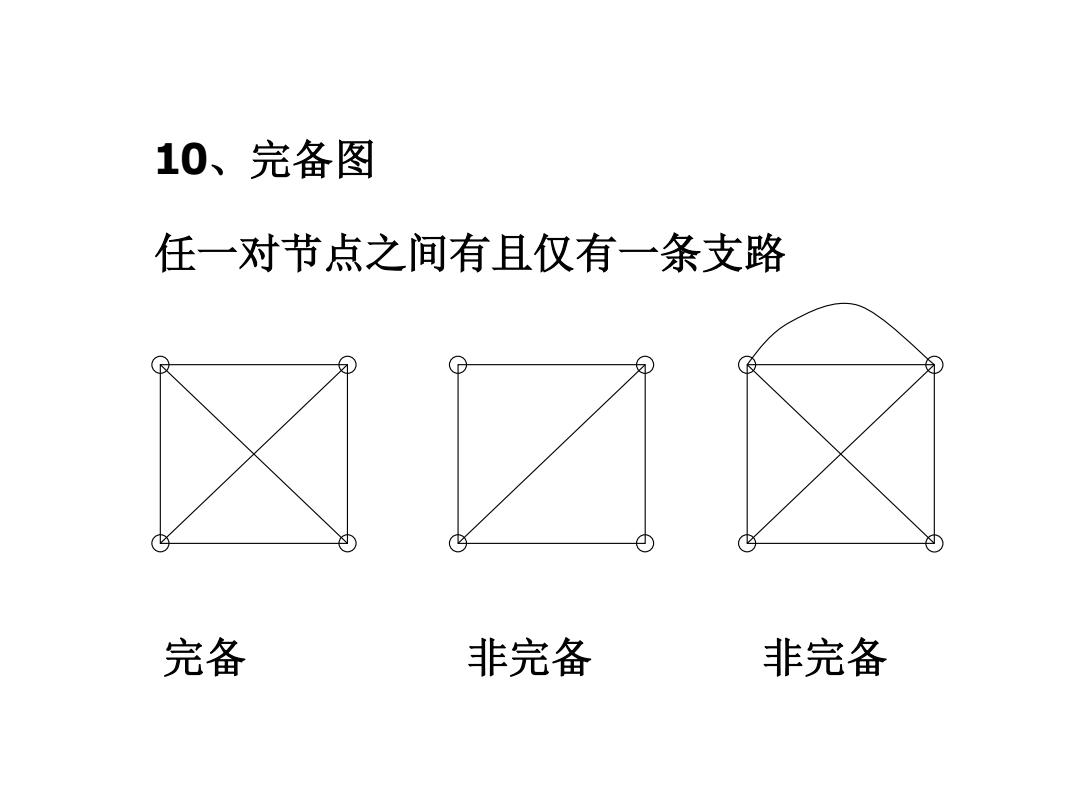
10、完备图 任一对节点之间有且仅有一条支路 ® 完备 非完备 非完备
10、完备图 任一对节点之间有且仅有一条支路 完备 非完备 非完备