电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第17讲 电抗梯形滤波器综合（无源双口网络参数——电抗二端口综合）

第17讲1 电抗二端口综合 第九章：电抗梯形滤波器综合(1) 9-1、9-3和9-4三节。 第9章内容：第17-18讲

第17讲 电抗二端口综合 第9章内容：第17-18讲 第九章:电抗梯形滤波器综合（1） 9-1、9-3和9-4三节

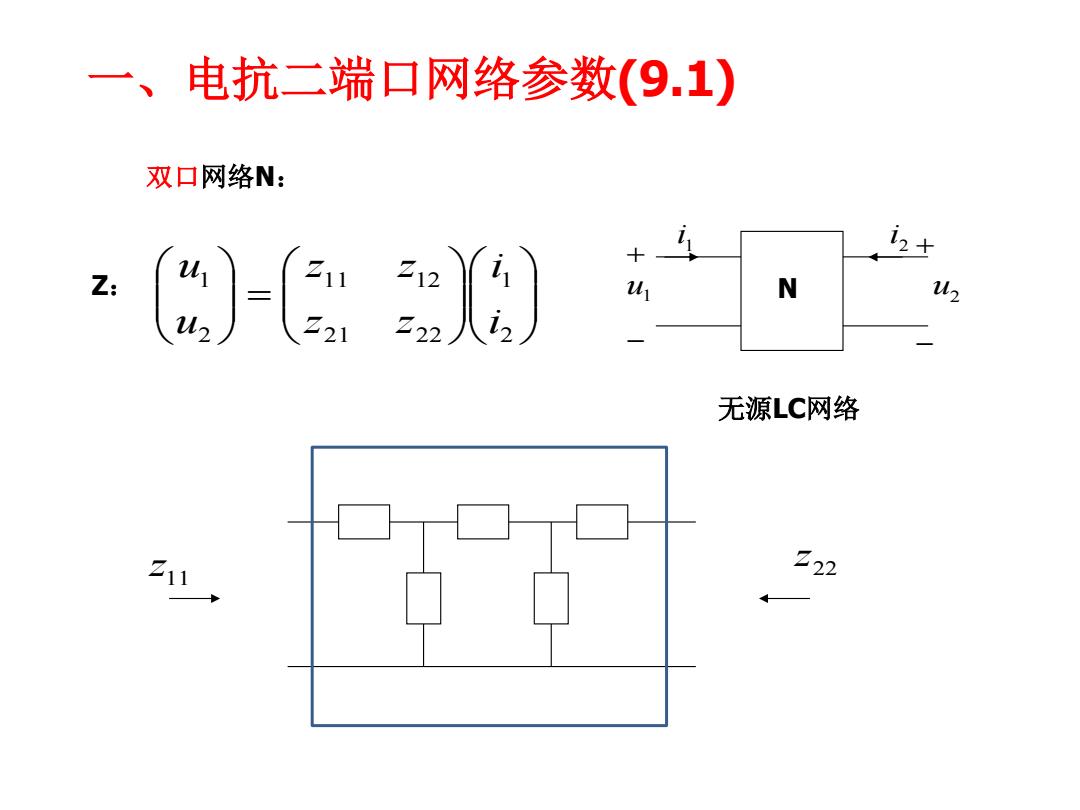
一、电抗二端口网络参数(9.1) 双口网络N: i Z: N u2 无源LC网络 22

一、电抗二端口网络参数(9.1) 双口网络N：   u1 u2 1 i N 2 i 无源LC网络                           2 1 21 22 11 12 2 1 i i z z z z u u Z： 11 z 22 z

十 i2 Y: )- N 2 无源LC网络 y11

Y ： u1 u2 1i N 2 i 无源LC网络       21 21 22 11 12 21 uu y y y y ii 11 y

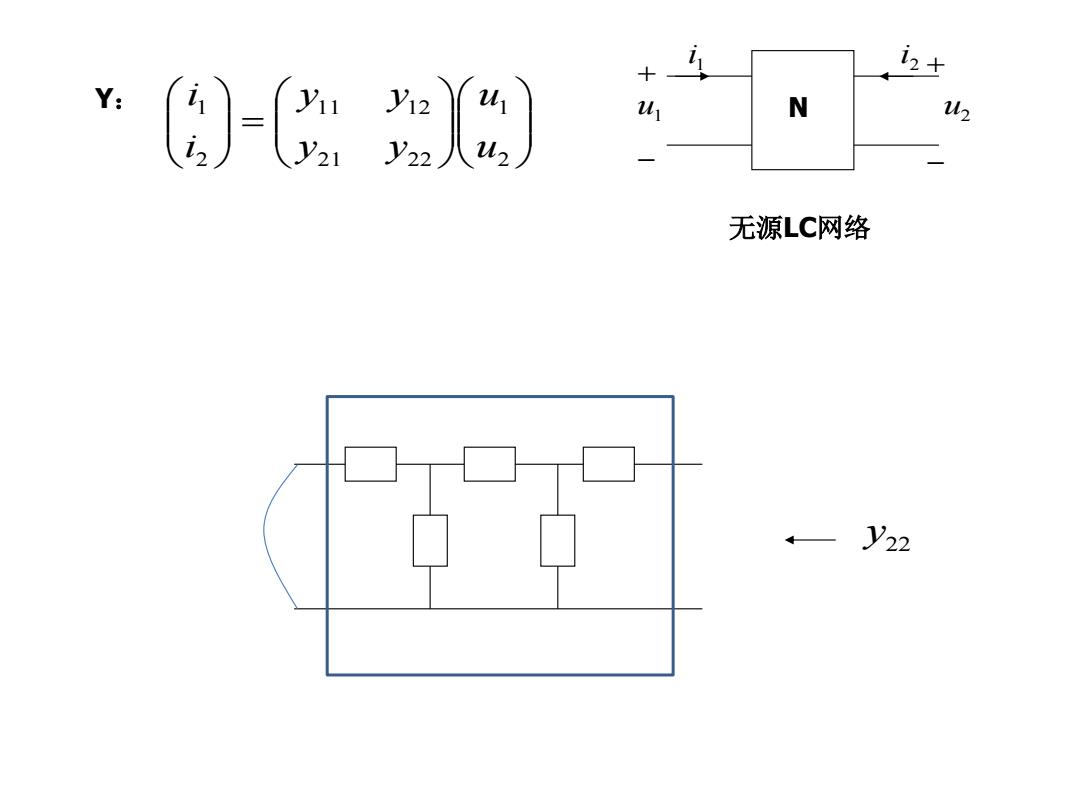
十 Y: )- u N 2 无源LC网络 —y22

Y ： u1 u2 1i N 2 i 无源LC网络       21 21 22 11 12 21 uu y y y y ii 22 y

-0- Z11(S) Z22(S) Y11(s) Y22(s)

                        2 1 21 22 11 12 2 1 u u y y y y i i                         2 1 21 22 11 12 2 1 i i z z z z u u Z11(s) Z22(s) Y11(s) Y22(s)

问题： 1、如何找到这四个参数？ Z1(S) Z22(S) Y1(S) Y22(s) 2、四个函数可能综合出四个网络，如何 确认娜个是正确合理的？

问题： 1、如何找到这四个参数？ Z11(s) Z22(s) Y11(s) Y22(s) 2、四个函数可能综合出四个网络，如何 确认哪个是正确合理的？                         2 1 21 22 11 12 2 1 u u y y y y i i                         2 1 21 22 11 12 2 1 i i z z z z u u

i2 u N 1W2 如何先找出四个参数？ H(S)= U(s) 2 U3(s) Z1(s) Z22(S) Y11(s) Y22(S)

  u1 u2 1 i N 2 i   如何先找出四个参数？ ( ) ( ) ( ) 2 1 U s U s H s  Z11(s) Z22(s) Y11(s) Y22(s) ？

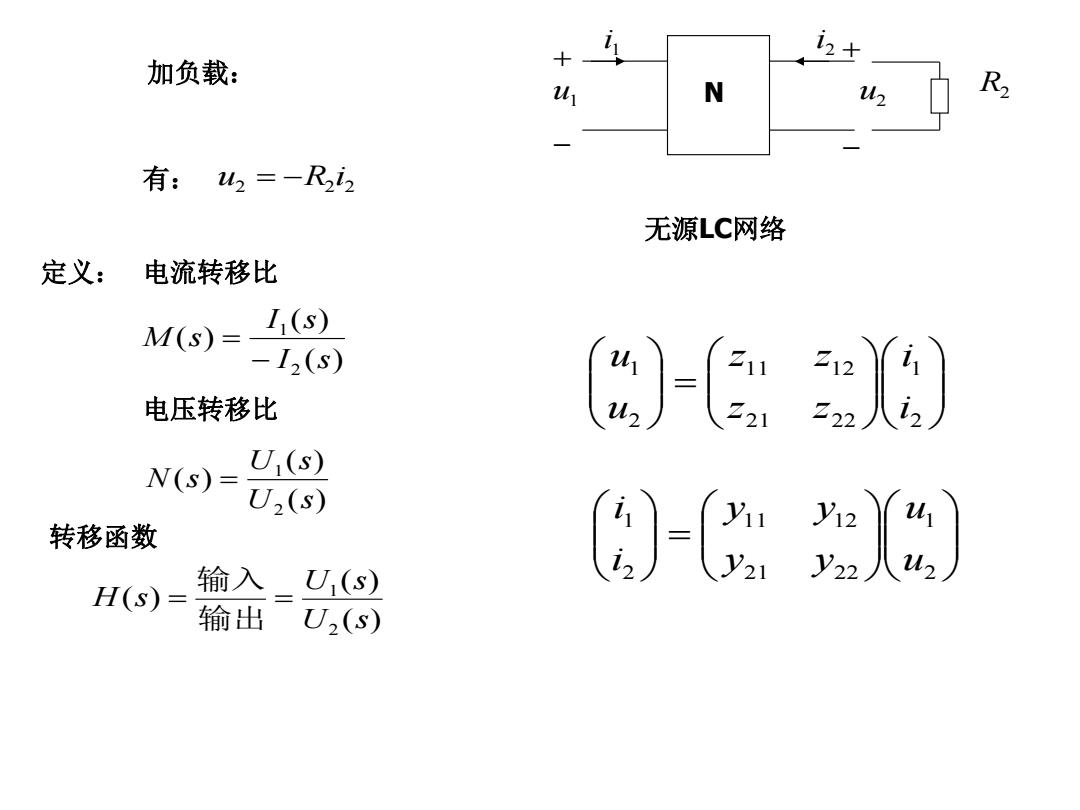
12 加负载： u N 2 R2 有：2=-R2i2 无源LC网络 定义： 电流转移比 M(s)= I1(S) -I,(s) 电压转移比 W-E 20 N(s)= U(s) U,(s) 转移函数 H(s)= 输入 )- U1(s) 输出 U,(s)

加负载： 2 2 2 u  R i 定义： 有：   u1 u2 1 i N 2 i 无源LC网络 R2                           2 1 21 22 11 12 2 1 i i z z z z u u                         2 1 21 22 11 12 2 1 u u y y y y i i ( ) ( ) ( ) 2 1 I s I s M s   ( ) ( ) ( ) 2 1 U s U s N s  电流转移比 电压转移比 ( ) ( ) ( ) 2 1 U s U s H s   输出 输入 转移函数

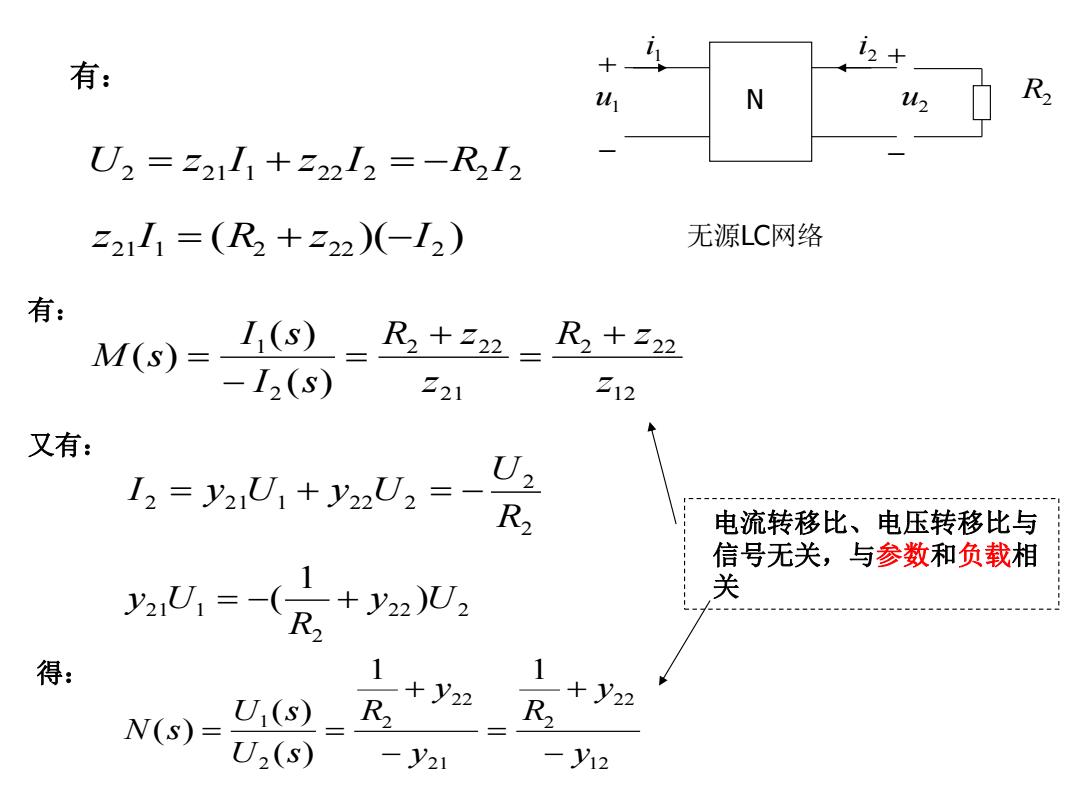
1 有： + N R2 UU2=22111+2222=-R212 221I1=(R2+222)(-I2) 无源LC网络 有： M(S)= I(s)=,+2= R2+222 -I2(s) z21 Z12 又有： 1=y0,+U2= U2 R2 电流转移比、电压转移比与 信号无关，与参数和负载相 ,=-(尺+， 关 得： 1 V)= U1(s)_R2 +y22 1+y22 U2(s) -V21 -y12

有：   2 2 2 21 1 22 2 R U I  y U  y U   又有： 有： u1 u2 1 i N 2 i 无源LC网络 R2   2 21 1 22 2 2 2 U  z I  z I  R I ( )( ) 21 1 2 22 2 z I  R  z I 12 2 22 21 2 22 2 1 ( ) ( ) ( ) z R z z R z I s I s M s       12 22 2 21 22 2 2 1 1 1 ( ) ( ) ( ) y y R y y R U s U s N s        22 2 2 21 1 ) 1 ( y U R y U    得： 电流转移比、电压转移比与 信号无关，与参数和负载相 关

+y22(S) M(s)= R2+222(S) R N(S)= 212(S) -y2(S) 由LC构成的电抗网络，其函数的实部必为零，又由（7- 2-10/11)的知识，实部等于偶函数，虚部等于奇函数， 因此，网络的参数必为奇函数。 奇函数有： 212(-S)=-212(S) M(-3)= R2+z22(-S)R2-z22(S) 212(-S) -212(S) 又有： M(s)=B+222(s) 212(S) 得： M(S)z12(S)-222(S)=R2 -M(-S)z12(S)+222(S)=R2

( ) ( ) 12 12 z s  z s 由LC构成的电抗网络，其函数的实部必为零，又由（7- 2-10/11）的知识，实部等于偶函数，虚部等于奇函数， 因此，网络的参数必为奇函数。 ( ) ( ) ( ) 12 2 22 z s R z s M s   ( ) ( ) 1 ( ) 12 22 2 y s y s R N s    又有： 奇函数有： ( ) ( ) ( ) ( ) ( ) 12 2 22 12 2 22 z s R z s z s R z s M s         ( ) ( ) ( ) 12 2 22 z s R z s M s   12 22 2 12 22 2 ( ) ( ) ( ) ( ) ( ) ( ) M s z s z s R M s z s z s R     得：  