
第13章核磁共振波谱分析法 Nuclear Magnetic Resonance Spectroscopy,NMR
第13章 核磁共振波谱分析法 Nuclear Magnetic Resonance Spectroscopy,NMR

13-1概述 将有磁性的自旋原子核放入强磁场中,以 适当频率的电磁波辐射,原子核吸收射频 辐射发生能级跃迁,产生核磁共振吸收现 象,从而获得有关化合物分子骨架信息, 这种方法称为核磁共振波谱分析法。 以1H为研究对象获得的谱图称为氢谱,记 做H-NMR;以13C为研究对象获得的谱图 称为碳谱,记做13C-NMR
13-1 概述 将有磁性的自旋原子核放入强磁场中,以 适当频率的电磁波辐射,原子核吸收射频 辐射发生能级跃迁,产生核磁共振吸收现 象,从而获得有关化合物分子骨架信息, 这种方法称为核磁共振波谱分析法。 以1H为研究对象获得的谱图称为氢谱,记 做1H-NMR;以13C为研究对象获得的谱图 称为碳谱,记做13C –NMR

20世纪40年代中期,以两位美国科学家Bloch和Purcell为首的 研究小组几乎同时发现核磁共振现象。因此,他们两人获得 1952年的诺贝尔物理奖 ■1953年,美国Varian?公司研制成功第一台商品化的核磁共振仪 (30MHz); ■1966年高分辨率核磁共振仪问世; ■1991年诺贝尔化学奖单独授予瑞士科学家rnst; 2002年诺贝尔化学奖授予瑞士科学家Wuithrich,表彰他利用多 维核磁共振技术在测定溶液中生物大分子三维结构方面的开创 性贡献
20世纪40年代中期,以两位美国科学家Bloch和 Purcell为首的 研究小组几乎同时发现核磁共振现象。因此,他们两人获得 1952年的诺贝尔物理奖; 1953年,美国Varian公司研制成功第一台商品化的核磁共振仪 (30MHz); 1966年高分辨率核磁共振仪问世; 1991年诺贝尔化学奖单独授予瑞士科学家Ernst; 2002年诺贝尔化学奖授予瑞士科学家Wüthrich,表彰他利用多 维核磁共振技术在测定溶液中生物大分子三维结构方面的开创 性贡献
N 用能量等于△E的电磁波照射 磁场中的磁性核,则低能级 上的某些核会被激发到高能 级上去(或核自旋由与磁场 S 平行方向转为反平行)。 MR→利用磁场中的磁性原子核吸收电磁波时 产生的能级分裂与共振现象
用能量等于E的电磁波照射 磁场中的磁性核,则低能级 上的某些核会被激发到高能 级上去(或核自旋由与磁场 平行方向转为反平行)。 NMR利用磁场中的磁性原子核吸收电磁波时 产生的能级分裂与共振现象。 N S N S S N N S

核磁共振基本原理 质量数为奇数,质子数为奇数或偶数的核是磁性, 如H、13,C、1,F等I=1/2;B、5,C1等原子核 的I=3/2 ■质量数为偶数,质子数也为偶数的核不是磁性的 I=0 目前主要研究I=1/2的核,如H,13C等
核磁共振基本原理 质量数为奇数,质子数为奇数或偶数的核是磁性, 如1 1H、13 6C、19 9F等I=1/2;11 5B、35 17Cl等原子核 的I=3/2 质量数为偶数,质子数也为偶数的核不是磁性的, I=0 目前主要研究I=1/2的核,如1H, 13C等

核磁共振基本原理 一亭篆餐禁芥磁场中,与外磁场相互作用,核磁矩有不同取向,可用磁量 m=1,-1,1-2,-I 每种取向对应一种能量, E=(-mμ/I)Bo 1H在外磁场中只有m=1/2及m=-1/2两种取向 m=1/2 E12=-1/2(Bo)/1/2=-μB0 m=-1/2 E-12=1/2(uBo)/1/2=BBo 低能态(m=1/2),核磁矩与外磁场同向,高能态(m=-1/2)核磁矩与外磁方 向相反 AE=E-1n一E12=2βB0
核磁共振基本原理 自旋核在外磁场中,与外磁场相互作用,核磁矩有不同取向,可用磁量 子数表示。 m = I, I-1, I-2 , .-I 每种取向对应一种能量, E=(-mμ/I)βB0 1H在外磁场中只有m=1/2及m=-1/2两种取向 m=1/2 E1/2= -1/2(μβB0 )/1/2=-μβB0 m=-1/2 E-1/2 = 1/2(μβB0 )/1/2=μβB0 低能态(m=1/2),核磁矩与外磁场同向,高能态(m=-1/2)核磁矩与外磁方 向相反 ΔE=E-1/2-E1/2 =2 μβB0

△E= 对氢核I=1/2△E=2uB0 摩尔进动(Larmor precession.):原子核一边自旋, 一边围绕外加磁场方向回旋。 拉摩尔进动时有一定的频率,称为拉摩尔进动频率
对氢核I=1/2 ∆E=2μB0 摩尔进动(Larmor precession):原子核一边自旋, 一边围绕外加磁场方向回旋。 拉摩尔进动时有一定的频率,称为拉摩尔进动频率。 I B E 0
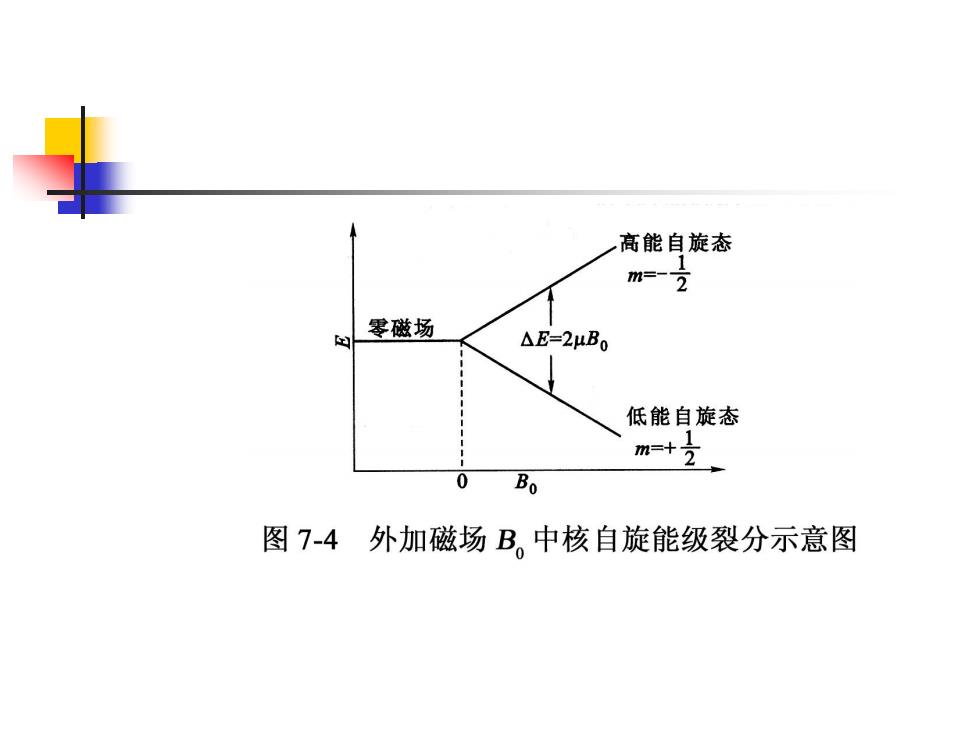
高能自旋态 m=-立 零磁场 △E=2μB0 低能自旋态 m+之 0 Bo 图7-4外加磁场B。中核自旋能级裂分示意图

w=2πy=yB。 2π 上式被称为核磁共振方程或核磁共振条件。 (1)不同的原子核,y不同,发生共振的条件不同。当 B。一定时,值大的原子核,在相同磁场强度下发生 核磁能级跃迁时的射频波频率高;反之,值小的原子 核,在相同磁场强度下发生核磁能级跃迁时的射频波 频率低
ω0 =2πν0 =γB0 上式被称为核磁共振方程或核磁共振条件。 (1)不同的原子核,γ不同,发生共振的条件不同。当 B0一定时, γ值大的原子核,在相同磁场强度下发生 核磁能级跃迁时的射频波频率高;反之,γ值小的原子 核,在相同磁场强度下发生核磁能级跃迁时的射频波 频率低, 2 0 0 B

当用一定能量的射频电磁波照射原子核,当外加 磁感应强度达到某一数值时,能量满足下式: △E=2uBo=hv 核吸收能量,产生跃迁,发生核磁共振现象
当用一定能量的射频电磁波照射原子核,当外加 磁感应强度达到某一数值时,能量满足下式: ∆E=2μB0 =hν 核吸收能量,产生跃迁,发生核磁共振现象