
《微积分11》课程教学大纲 一、课程基本信息 课程代码:16073004 课程名称:微积分I1 英文名称:Caleulus II 课程类别:公共课 学 时:64 学 分:4 适用对象:创业教育学院本科生 考核方式:考试 先修课程:微积分】 二、课程简介 《微积分Ⅱ》是经济管理诸学科都需开设的一门重要的基础理论课程,也是硕士 研究生入学全国统一考试中数学科目中必考的数学课程之一。本课程主要内容包括: )一元函数积分学中的定积分内容;(②)多元函数微积分学;(3)无穷级数:(4)常微分方 程。该课程所体现的数量的变与不变的规律和关系、从具体概念抽象出来的公理化方 法、以及严谨的逻辑推证、巧妙的归纳综合等,对于强化学生的数学训练,培养学生 的逻辑推理和抽象思维能力、空间直观和想象能力具有重要的作用。另外作为一门重 要的方法和工具性课程,随着计算机及其应用技术的飞速发展,微积分这门课程的作 用与地位显得日益重要。另外它是线性代数、概率论与数理统计等后续课程的必要基 础。 Calculus II is the discipline of economics and management are required to set up ar important basic theoretical course,is also a graduate student entrance in the unified national examination mathematics subject in the study of one of the mathematics curriculum.The main contents of this course include:the integral content of the integral calculus of unitary functions:Multivariate function calculus.The infinite series:The ordinary differential equation.This course embodies the number of rules and relations of change and status quo, from the concrete concept of abstracting the axiomatic method,and the rigorous logic inferred.clever inductive synthesis.etc..to strengthen the students'mathematics training. cultivate students logical reasoning and intuitive and abstract thinking ability,space imagination ability plays an important role.With the rapid development of computer and its application technology,the role and status of the course are becoming more and more important.In addition,it is a necessary basis for the following courses of linear algebra
1 《微积分 II》课程教学大纲 一、课程基本信息 课程代码:16073004 课程名称:微积分 II 英文名称: Calculus II 课程类别: 公共课 学 时: 64 学 分:4 适用对象: 创业教育学院本科生 考核方式:考试 先修课程:微积分 I 二、课程简介 《微积分 II》是经济管理诸学科都需开设的一门重要的基础理论课程,也是硕士 研究生入学全国统一考试中数学科目中必考的数学课程之一。本课程主要内容包括: ⑴一元函数积分学中的定积分内容;⑵多元函数微积分学;⑶无穷级数;⑷常微分方 程。该课程所体现的数量的变与不变的规律和关系、从具体概念抽象出来的公理化方 法、以及严谨的逻辑推证、巧妙的归纳综合等,对于强化学生的数学训练,培养学生 的逻辑推理和抽象思维能力、空间直观和想象能力具有重要的作用。另外作为一门重 要的方法和工具性课程,随着计算机及其应用技术的飞速发展,微积分这门课程的作 用与地位显得日益重要。另外它是线性代数、概率论与数理统计等后续课程的必要基 础。 Calculus II is the discipline of economics and management are required to set up an important basic theoretical course, is also a graduate student entrance in the unified national examination mathematics subject in the study of one of the mathematics curriculum. The main contents of this course include: the integral content of the integral calculus of unitary functions; Multivariate function calculus; The infinite series; The ordinary differential equation. This course embodies the number of rules and relations of change and status quo, from the concrete concept of abstracting the axiomatic method, and the rigorous logic inferred, clever inductive synthesis, etc., to strengthen the students' mathematics training, cultivate students' logical reasoning and intuitive and abstract thinking ability, space imagination ability plays an important role. With the rapid development of computer and its application technology, the role and status of the course are becoming more and more important. In addition, it is a necessary basis for the following courses of linear algebra

probability theory and mathematical statistics. 三、课程性质与教学目的 1、本课程是经济数学基础之一,授课对象为本科经济类和管理类专业学生。在讲 授和学习时,应注重提高学生分析问题和解决问题的能力,培养学生良好的逻辑思维 习惯,让学生掌握全面考虑问题的思维方法,这将有助于学生们顺利地学习其他专业 理论课。哲学中的对立统一规律、量变质变规律、否定之否定规律在《微积分》中时 有体现。通过课程内容,让学生加强辩证唯物主义思维训练:通过数学历史,让学生 感受科学家的奋斗精神。 2、本课程主要内容包括:()一元函数积分学中的定积分内容:(2)多元函数微积 分学:(③)无穷级数:(④)常微分方程。 3、本大纲的教学总时数为64学时(含习题课),各章节教学时数的具体分配, 请参考附表。 4、本课程以课堂讲授为主,讨论辅导为辅,课堂练习与课外作业相结合。 5、在制定本教学大纲时,为了明确对教学大纲中所列具体内容的要求程度,将 本要求分为由低到高的三个等级,即对概念和理论性的知识,低到高分别用“知道”、 “了解”、“理解”三级区分,对运算、方法和应用方面的知识,由低到高分别用“会 或能”、“掌握”、“热练掌握”三级区分 四、教学内容及要求 第六章 定积分 〖教学内容】 §6.1定积分的概念与性质 曲边梯形的面积、定积分定义与几何意义、定积分的基本性质、积分中值定理。 §6.2微积分基本定理 变上限积分、原函数存在性定理、变限积分求导及牛顿一莱布尼兹公式。 §6.3定积分的计算 定积分的第一与第二换元法、定积分的分部积分法。 §6.4定积分的应用 平面图形的面积、旋转体的体积、简单的经济应用 §6.5广义积分初步
2 probability theory and mathematical statistics. 三、课程性质与教学目的 1、本课程是经济数学基础之一,授课对象为本科经济类和管理类专业学生。在讲 授和学习时,应注重提高学生分析问题和解决问题的能力,培养学生良好的逻辑思维 习惯,让学生掌握全面考虑问题的思维方法,这将有助于学生们顺利地学习其他专业 理论课。哲学中的对立统一规律、量变质变规律、否定之否定规律在《微积分》中时 有体现。通过课程内容,让学生加强辩证唯物主义思维训练;通过数学历史,让学生 感受科学家的奋斗精神。 2、本课程主要内容包括:⑴一元函数积分学中的定积分内容;⑵多元函数微积 分学;⑶无穷级数;⑷常微分方程。 3、本大纲的教学总时数为 64 学时(含习题课),各章节教学时数的具体分配, 请参考附表。 4、本课程以课堂讲授为主,讨论辅导为辅,课堂练习与课外作业相结合。 5、在制定本教学大纲时,为了明确对教学大纲中所列具体内容的要求程度,将 本要求分为由低到高的三个等级,即对概念和理论性的知识,低到高分别用“知道”、 “了解”、“理解”三级区分,对运算、方法和应用方面的知识,由低到高分别用“会 或能”、“掌握”、“熟练掌握”三级区分。 四、教学内容及要求 第六章 定积分 〖教学内容〗 §6.1 定积分的概念与性质 曲边梯形的面积、定积分定义与几何意义、定积分的基本性质、积分中值定理。 §6.2 微积分基本定理 变上限积分、原函数存在性定理、变限积分求导及牛顿—莱布尼兹公式。 §6.3 定积分的计算 定积分的第一与第二换元法、定积分的分部积分法。 §6.4 定积分的应用 平面图形的面积、旋转体的体积、简单的经济应用。 §6.5 广义积分初步

无穷积分和瑕积分的概念、收敛与发散的定义、敛散性判别及无穷积分和瑕积分 的计算。 〖教学目的与要求刀 1.了解定积分的概念和基本性质,理解积分中值定理。可以指出,定积分的本质 是连续型无限求和,从有限到无限,是一类事物发展的必然规律,是人类认识论历史 发展的重要进步。 2.理解变上限定积分,掌握求变上限定积分导数的方法。这里需要强调,变量与 常量是相对概念,它们是对立统一的。应该用运动和发展的思维方式,分析和解决问 题。 3.熟练掌握牛顿一莱布尼兹公式。 4.熟练掌握定积分的换元积分法与分部积分法。 5.掌握用定积分计算平面图形面积、以及平面图形绕坐标轴旋转所得旋转体的体 6.了解广义积分的概念,了解广义积分敛散的条件及其计算方法。 〖重点与难点】 1.本章重点内容包括:定积分的定义:变限积分及其导数:定积分的计算(主要 是换元法和分部积分法):定积分在几何和经济中的应用:定积分性质及积分中值定 理;广义积分敛散的概念,广义积分计算。 2.本章难点包括:定积分的定义:变限积分的应用:定积分的换元积分法:积分 中值定理的应用:广义积分的敛散性判别。 〖教学时数与教学方法刀 共14学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议】 勤学多练。熟练掌握定积分的计算,掌握用定积分计算平面图形的面积和旋转体 的体积,掌握定积分在经济中的简单应用。 第七章 多元微积分学 〖教学内容〗 s7.1预备知识
3 无穷积分和瑕积分的概念、收敛与发散的定义、敛散性判别及无穷积分和瑕积分 的计算。 〖教学目的与要求〗 1.了解定积分的概念和基本性质,理解积分中值定理。可以指出,定积分的本质 是连续型无限求和,从有限到无限,是一类事物发展的必然规律,是人类认识论历史 发展的重要进步。 2.理解变上限定积分,掌握求变上限定积分导数的方法。这里需要强调,变量与 常量是相对概念,它们是对立统一的。应该用运动和发展的思维方式,分析和解决问 题。 3.熟练掌握牛顿—莱布尼兹公式。 4.熟练掌握定积分的换元积分法与分部积分法。 5.掌握用定积分计算平面图形面积、以及平面图形绕坐标轴旋转所得旋转体的体 积。 6.了解广义积分的概念,了解广义积分敛散的条件及其计算方法。 〖重点与难点〗 1.本章重点内容包括:定积分的定义;变限积分及其导数;定积分的计算(主要 是换元法和分部积分法);定积分在几何和经济中的应用;定积分性质及积分中值定 理;广义积分敛散的概念,广义积分计算。 2.本章难点包括:定积分的定义;变限积分的应用;定积分的换元积分法;积分 中值定理的应用;广义积分的敛散性判别。 〖教学时数与教学方法〗 共 14 学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议〗 勤学多练。熟练掌握定积分的计算,掌握用定积分计算平面图形的面积和旋转体 的体积,掌握定积分在经济中的简单应用。 第七章 多元微积分学 〖教学内容〗 §7.1 预备知识

空间直角坐标系、空间点与坐标的关系、空间曲线与曲面方程、平面上的区域、 区域的边界、点的邻域、开区域与闭区域的概念。 §7.2多元函数的概念 多元函数的定义、二元函数的定义域与几何意义、二元函数的极限与连续性。 §7.3偏导数与全微分 偏导数的定义、几何意义与计算方法、全微分的定义与计算方法。 §7.4高阶偏导数 高阶偏导数的定义与计算,混合偏导数的计算。 §7.5多元复合函数与隐函数微分法 多元复合函数微分法(链式规则)、多元隐函数微分法。 §7.6多元函数的极值与最值 二元函数极值的定义、极值存在的必要条件与充分条件、条件极值的概念与拉格 朗日乘数法、多元函数的最值的概念与求法、最小二乘法。 §7.7二重积分 曲顶柱体的体积、二重积分的定义及其基本性质、二重积分化为二次积分、二次 积分改变积分顺序的方法、在直角坐标系与极坐标系下计算二重积分的方法。 【教学目的与要求〗 1.了解空间直角坐标系的有关概念,会画简单的空间图形,理解平面区域,区域 的边界,点的邻域,开区域与闭区域等概念。 2.理解多元函数的概念,掌握二元函数的定义和定义域的求法,理解二元函数的 几何意义。 3.了解二元函数的极限与连续性的概念。注意,极限是典型的运动与发展的结果, 不可用静止的眼光看待它。它体现了哲学中的量变质变规律。 4.理解多元函数的偏导数与全微分的概念,熟练掌握求一阶偏导数与全微分的方 法。 5.掌握二元函数高阶偏导数的概念和计算方法。 6.掌握多元复合函数与隐函数的偏导数求法。 7.理解二元函数的极值与条件极值的概念,掌握用二元函数极值存在的必要条件 与充分条件求二元函数极值的方法,熟练掌握用拉格朗日乘数法求二元函数条件极值 的方法。这里需要强调,极值与最大值最小值之间的关系是局部与整体的辩证关系
4 空间直角坐标系、空间点与坐标的关系、空间曲线与曲面方程、平面上的区域、 区域的边界、点的邻域、开区域与闭区域的概念。 §7.2 多元函数的概念 多元函数的定义、二元函数的定义域与几何意义、二元函数的极限与连续性。 §7.3 偏导数与全微分 偏导数的定义、几何意义与计算方法、全微分的定义与计算方法。 §7.4 高阶偏导数 高阶偏导数的定义与计算,混合偏导数的计算。 §7.5 多元复合函数与隐函数微分法 多元复合函数微分法(链式规则)、多元隐函数微分法。 §7.6 多元函数的极值与最值 二元函数极值的定义、极值存在的必要条件与充分条件、条件极值的概念与拉格 朗日乘数法、多元函数的最值的概念与求法、最小二乘法。 §7.7 二重积分 曲顶柱体的体积、二重积分的定义及其基本性质、二重积分化为二次积分、二次 积分改变积分顺序的方法、在直角坐标系与极坐标系下计算二重积分的方法。 〖教学目的与要求〗 1.了解空间直角坐标系的有关概念,会画简单的空间图形,理解平面区域,区域 的边界,点的邻域,开区域与闭区域等概念。 2.理解多元函数的概念,掌握二元函数的定义和定义域的求法,理解二元函数的 几何意义。 3.了解二元函数的极限与连续性的概念。注意,极限是典型的运动与发展的结果, 不可用静止的眼光看待它。它体现了哲学中的量变质变规律。 4.理解多元函数的偏导数与全微分的概念,熟练掌握求一阶偏导数与全微分的方 法。 5.掌握二元函数高阶偏导数的概念和计算方法。 6.掌握多元复合函数与隐函数的偏导数求法。 7.理解二元函数的极值与条件极值的概念,掌握用二元函数极值存在的必要条件 与充分条件求二元函数极值的方法,熟练掌握用拉格朗日乘数法求二元函数条件极值 的方法。这里需要强调,极值与最大值最小值之间的关系是局部与整体的辩证关系

8.理解二元重积分的概念,了解二重积分的几何意义和基本性质,熟练掌握在直 角坐标系下计算二重积分的常规方法,掌握极坐标系下二重积分的计算。这里可启发 学生,各类关于定积分及二重积分的应用背景都是具体的现象,而它们所具有的共性 才是问题的本质。透过现象看本质,是辩证唯物主义的重要方法。 〖重点与难点】 1,本章重点内容包括:多元复合函数求导法:隐函数求导法:全微分计算:无条 件极值与条件极值:二重积分。 2.本章难点包括:多元复合函数求导法:含隐函数的全微分计算:二重积分的计 算。 〖教学时数与教学方法〗 共24学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议】 勤学多练。熟练掌握求一阶偏导数与全微分的方法,掌握多元复合函数与隐函数 的偏导求法,熟练掌握用拉格朗日乘数法求二元函数条件极值的方法,熟练掌握在直 角坐标下计算二重积分的常规方法。 第八章 无穷级数 《教学内容】 §8.1常数项级数的概念和性质 无穷级数及其一般项与部分和的概念、无穷级数收敛与发散的定义、收敛级数和 的概念、几何级数与调和级数的敛散性,无穷级数收敛的必要条件,收敛级数的基本 性质。 §8.2常数项级数的敛散性 正项级数的概念、正项级数收敛的充分必要条件、正项级数敛散性的比较判别法、 达朗贝尔比值判别法。 任意项级数的概念、交错级数的概念、交错级数敛散性的莱布尼兹判别法。 任意项级数的绝对收敛与条件收敛的概念、绝对收敛与条件收敛的判别法。 s8.3幂级数
5 8.理解二元重积分的概念,了解二重积分的几何意义和基本性质,熟练掌握在直 角坐标系下计算二重积分的常规方法,掌握极坐标系下二重积分的计算。这里可启发 学生,各类关于定积分及二重积分的应用背景都是具体的现象,而它们所具有的共性 才是问题的本质。透过现象看本质,是辩证唯物主义的重要方法。 〖重点与难点〗 1.本章重点内容包括:多元复合函数求导法;隐函数求导法;全微分计算;无条 件极值与条件极值;二重积分。 2.本章难点包括:多元复合函数求导法;含隐函数的全微分计算;二重积分的计 算。 〖教学时数与教学方法〗 共 24 学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议〗 勤学多练。熟练掌握求一阶偏导数与全微分的方法,掌握多元复合函数与隐函数 的偏导求法,熟练掌握用拉格朗日乘数法求二元函数条件极值的方法,熟练掌握在直 角坐标下计算二重积分的常规方法。 第八章 无穷级数 〖教学内容〗 §8.1 常数项级数的概念和性质 无穷级数及其一般项与部分和的概念、无穷级数收敛与发散的定义、收敛级数和 的概念、几何级数与调和级数的敛散性,无穷级数收敛的必要条件,收敛级数的基本 性质。 §8.2 常数项级数的敛散性 正项级数的概念、正项级数收敛的充分必要条件、正项级数敛散性的比较判别法、 达朗贝尔比值判别法。 任意项级数的概念、交错级数的概念、交错级数敛散性的莱布尼兹判别法。 任意项级数的绝对收敛与条件收敛的概念、绝对收敛与条件收敛的判别法。 §8.3 幂级数

幂级数的概念、幂级数的收敛半径、收敛区间以及和函数的概念、幂级数的敛散 性的判别法、幂级数的收敛半径、收敛区间的求法、幂级数的基本性质。 §8.4函数的幂级数展开 泰勒级数、麦克劳林级数、泰勒公式及其余项。 幂级数展开定理,将函数展开成幂级数的方法(直接展开性,间接展开法)。 【教学目的与要求】 1.了解无穷级数及其一般项,部分和,收敛与发散,以及收敛级数的和等基本概 念。级数的本质是离散型无限求和,从有限到无限,是一类事物发展的必然规律,是 人类认识论历史发展的重要进步。它体现的是哲学中的量变质变规律。 2.掌握几何级数与级数的敛散性的判别条件,知道调和级数的敛散性。 3.掌握级数收敛的必要条件,以及收敛级数的基本性质。 4.掌握正项级数的比较判别法,熟练掌握正项级数的达朗贝尔比值判别法。 5.掌握交错级数的莱布尼兹判别法。 6.了解任意项级数绝对收敛与条件收敛的概念,掌握绝对收敛与条件收敛的判别 法。 7.了解函数项级数的概念,了解幂级数的收敛半径,收敛区间以及和函数的概念, 掌握幂级数的敛散性的判别法,熟练掌握收敛半径,收敛区间的求法,知道幂级数的 基本性质。 8.知道泰勒公式及其余项,了解泰勒级数与麦克劳林级数,了解幂级数展开定理; 掌握函数展开成幂级数的方法(直接展开法,间接展开法)。 〖重点与难点】 1.本章重点内容包括:常数项级数定义,性质及敛散性判定;幂级数的收敛半径 和收敛域:级数求和:将函数展开为幂级数。 2.本章难点包括:常数项级数的敛散性判定;级数求和:泰勒(Taylor)展开定 理:将函数展开为幂级数之间接法。 〖教学时数与教学方法〗 共12学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议】 勒学多练。掌握判定正项级数与交错级数敛散的各种方法:熟练掌握求幂级数收 敛半径,收敛区间和收敛域的方法,掌握将函数展开为幂级数的方法。 6
6 幂级数的概念、幂级数的收敛半径、收敛区间以及和函数的概念、幂级数的敛散 性的判别法、幂级数的收敛半径、收敛区间的求法、幂级数的基本性质。 §8.4 函数的幂级数展开 泰勒级数、麦克劳林级数、泰勒公式及其余项。 幂级数展开定理,将函数展开成幂级数的方法(直接展开性,间接展开法)。 〖教学目的与要求〗 1.了解无穷级数及其一般项,部分和,收敛与发散,以及收敛级数的和等基本概 念。级数的本质是离散型无限求和,从有限到无限,是一类事物发展的必然规律,是 人类认识论历史发展的重要进步。它体现的是哲学中的量变质变规律。 2.掌握几何级数与级数的敛散性的判别条件,知道调和级数的敛散性。 3.掌握级数收敛的必要条件,以及收敛级数的基本性质。 4.掌握正项级数的比较判别法,熟练掌握正项级数的达朗贝尔比值判别法。 5.掌握交错级数的莱布尼兹判别法。 6.了解任意项级数绝对收敛与条件收敛的概念,掌握绝对收敛与条件收敛的判别 法。 7.了解函数项级数的概念,了解幂级数的收敛半径,收敛区间以及和函数的概念, 掌握幂级数的敛散性的判别法,熟练掌握收敛半径,收敛区间的求法,知道幂级数的 基本性质。 8.知道泰勒公式及其余项,了解泰勒级数与麦克劳林级数,了解幂级数展开定理, 掌握函数展开成幂级数的方法(直接展开法,间接展开法)。 〖重点与难点〗 1.本章重点内容包括:常数项级数定义,性质及敛散性判定;幂级数的收敛半径 和收敛域;级数求和;将函数展开为幂级数。 2.本章难点包括:常数项级数的敛散性判定;级数求和;泰勒(Taylor)展开定 理;将函数展开为幂级数之间接法。 〖教学时数与教学方法〗 共 12 学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议〗 勤学多练。掌握判定正项级数与交错级数敛散的各种方法;熟练掌握求幂级数收 敛半径,收敛区间和收敛域的方法,掌握将函数展开为幂级数的方法

第九章 常微分方程初步 【教学内容〗 §9.1微分方程的基本概念 微分方程的定义、微分方程的阶、解(通解、特解)、定解条件和初值问题。 §9.2一阶微分方程 可分离变量方程、齐次方程、一阶线性微分方程。 §9.3高阶微分方程 二阶常系数线性微分方程的特征根解法,n阶线性微分方程的一般形式。 §9.4微分方程在经济学中的简单应用。 〖教学目的与要求】 1.了解微分方程的阶、通解、初始条件和特解等概念。 2.掌握可分离变量方程,齐次方程和一阶线性方程的求解方法。 3.会解二阶常系数齐次线性方程。 4.会解自由项为多项式,指数函数,正弦函数,余弦函数,以及它们的和与乘积 的二阶常系数非齐次线性微分方程。 5.会应用微分方程求一些简单的经济应用问题 【重点与难点】 1.本章重点内容包括:三类一阶微分方程的求解(可分离变量方程,齐次方程 一阶线性方程):二阶线性常系数齐次和非齐次方程求解:微分方程的应用。 2.本章难点包括:齐次方程,线性方程解的性质:二阶常系数非齐次方程的求解: 常数变易法。 【教学时数与教学方法〗 共10学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议】 勤学多练。熟练掌握一阶微分方程的求解方法,掌握解二阶常系数线性方程的方 法。 五、各教学环节学时分配
7 第九章 常微分方程初步 〖教学内容〗 §9.1 微分方程的基本概念 微分方程的定义、微分方程的阶、解(通解、特解)、定解条件和初值问题。 §9.2 一阶微分方程 可分离变量方程、齐次方程、一阶线性微分方程。 §9.3 高阶微分方程 二阶常系数线性微分方程的特征根解法, n 阶线性微分方程的一般形式。 §9.4 微分方程在经济学中的简单应用。 〖教学目的与要求〗 1.了解微分方程的阶、通解、初始条件和特解等概念。 2.掌握可分离变量方程,齐次方程和一阶线性方程的求解方法。 3.会解二阶常系数齐次线性方程。 4.会解自由项为多项式,指数函数,正弦函数,余弦函数,以及它们的和与乘积 的二阶常系数非齐次线性微分方程。 5.会应用微分方程求一些简单的经济应用问题。 〖重点与难点〗 1.本章重点内容包括:三类一阶微分方程的求解(可分离变量方程,齐次方程, 一阶线性方程);二阶线性常系数齐次和非齐次方程求解;微分方程的应用。 2.本章难点包括:齐次方程,线性方程解的性质;二阶常系数非齐次方程的求解; 常数变易法。 〖教学时数与教学方法〗 共 10 学时。以课堂讲授为主,辅导,练习为辅。 〖课外学习建议〗 勤学多练。熟练掌握一阶微分方程的求解方法,掌握解二阶常系数线性方程的方 法。 五、各教学环节学时分配
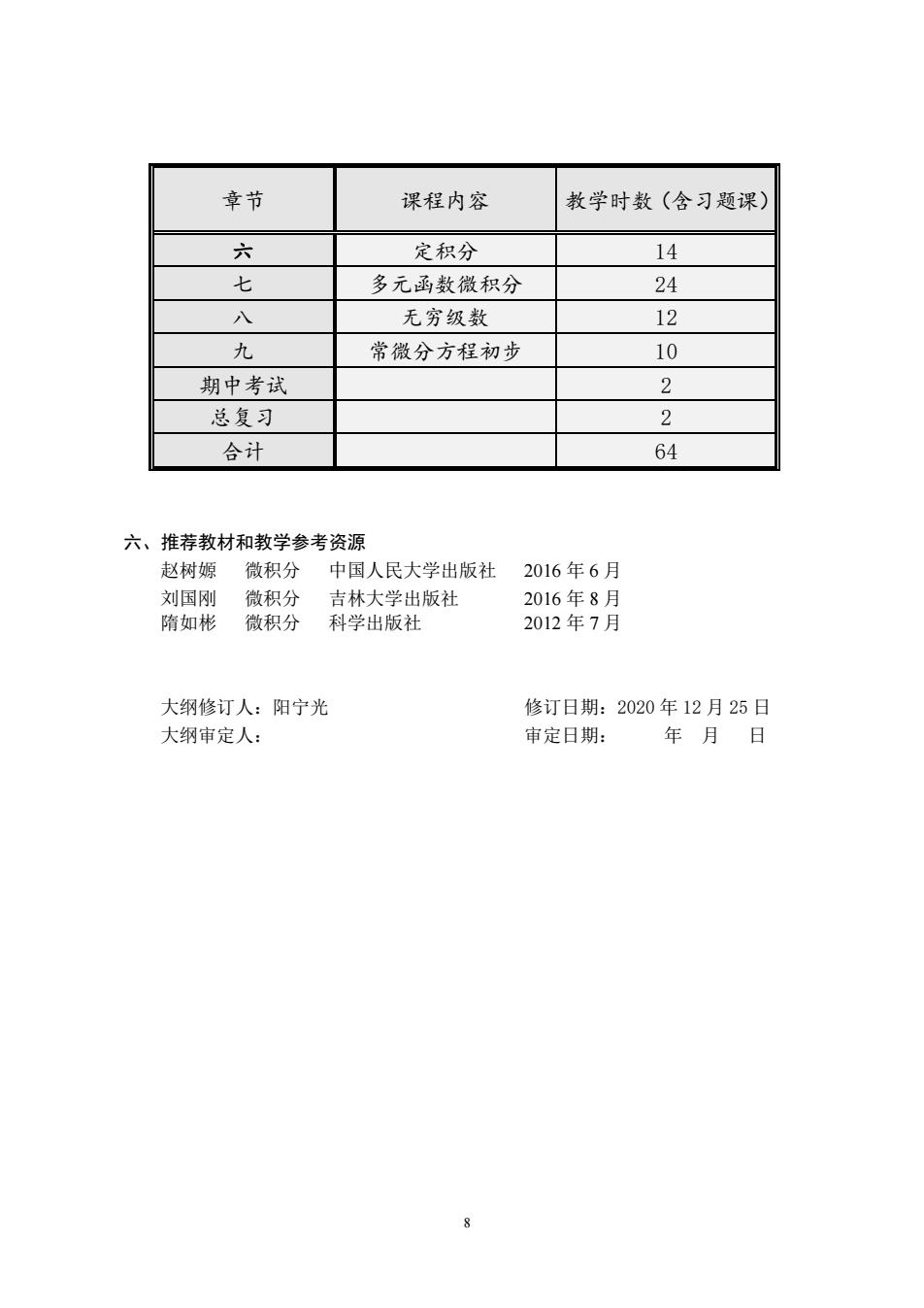
章节 课程内容 散学时数(含习题课) 六 定积分 14 七 多元函数微积分 24 八 无穷级数 12 九 常微分方程初步 10 期中考试 2 总复习 2 合计 64 六、推荐教材和教学参考资源 赵树嫖微积分中国人民大学出版社2016年6月 刘国刚微积分 吉林大学出版社 2016年8月 隋如彬微积分 科学出版社 2012年7月 大纲修订人:阳宁光 修订日期:2020年12月25日 大纲审定人: 审定日期: 年月日
8 章节 课程内容 教学时数(含习题课) 六 定积分 14 七 多元函数微积分 24 八 无穷级数 12 九 常微分方程初步 10 期中考试 2 总复习 2 合计 64 六、推荐教材和教学参考资源 赵树嫄 微积分 中国人民大学出版社 2016 年 6 月 刘国刚 微积分 吉林大学出版社 2016 年 8 月 隋如彬 微积分 科学出版社 2012 年 7 月 大纲修订人:阳宁光 修订日期:2020 年 12 月 25 日 大纲审定人: 审定日期: 年 月 日