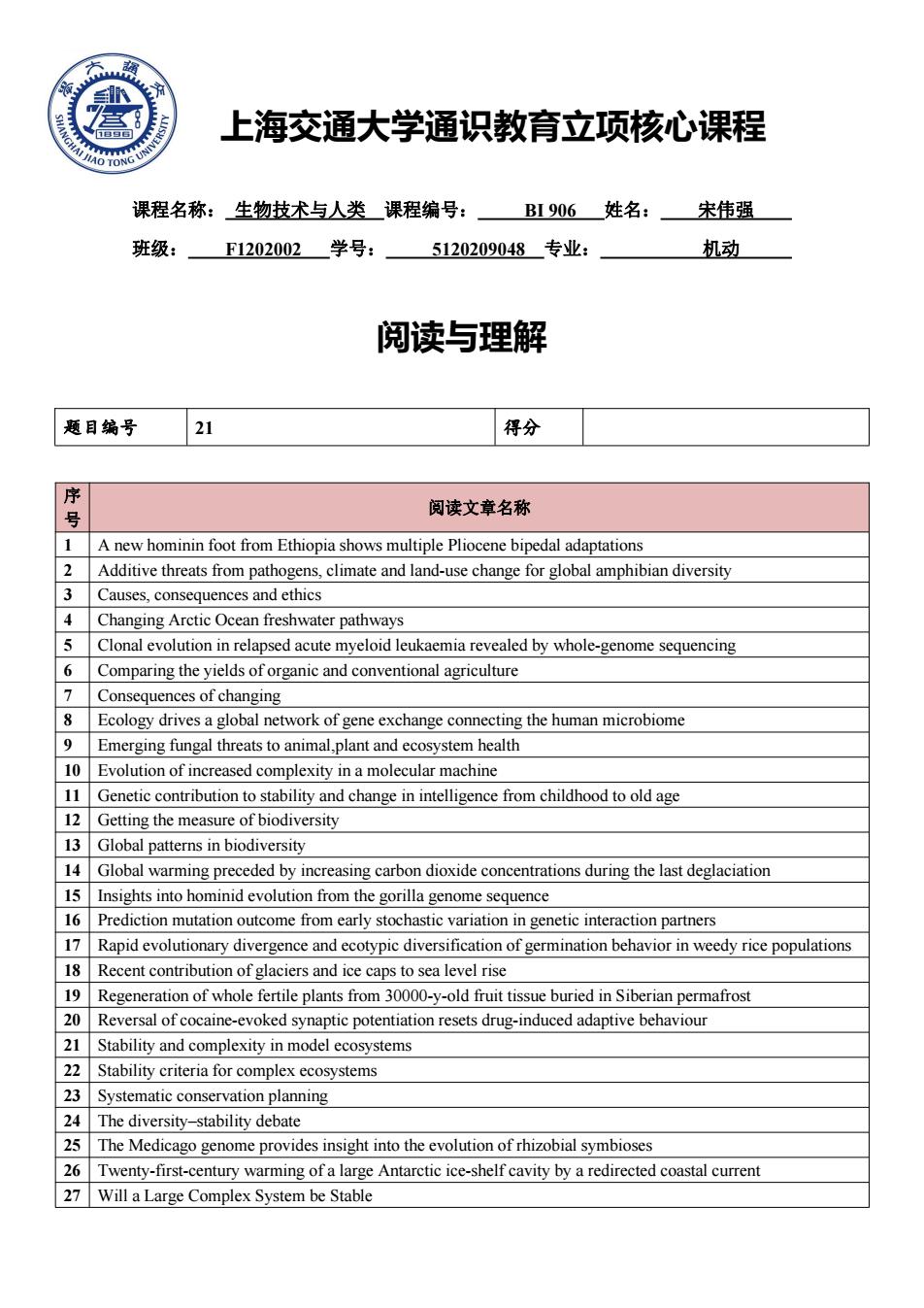
上海交通大学通识教育立项核心课程 课程名称:生物技术与人类课程编号: BI906姓名: 宋伟强 班级: F1202002学号: 5120209048专业: 机动 阅读与理解 题目编号 21 得分 序 阅读文章名称 1 A new hominin foot from Ethiopia shows multiple Pliocene bipedal adaptations 2 Additive threats from pathogens,climate and land-use change for global amphibian diversity 3 Causes,consequences and ethics 4 Changing Arctic Ocean freshwater pathways 5 Clonal evolution in relapsed acute myeloid leukaemia revealed by whole-genome sequencing 6 Comparing the yields of organic and conventional agriculture 7 Consequences of changing 8 Ecology drives a global network of gene exchange connecting the human microbiome 9 Emerging fungal threats to animal,plant and ecosystem health 10 Evolution of increased complexity in a molecular machine 11 Genetic contribution to stability and change in intelligence from childhood to old age 12 Getting the measure of biodiversity 13 Global patterns in biodiversity 14 Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation 15 Insights into hominid evolution from the gorilla genome sequence 16 Prediction mutation outcome from early stochastic variation in genetic interaction partners 17 Rapid evolutionary divergence and ecotypic diversification of germination behavior in weedy rice populations 18 Recent contribution of glaciers and ice caps to sea level rise 19 Regeneration of whole fertile plants from 30000-y-old fruit tissue buried in Siberian permafrost 20 Reversal of cocaine-evoked synaptic potentiation resets drug-induced adaptive behaviour 21 Stability and complexity in model ecosystems 22 Stability criteria for complex ecosystems 23 Systematic conservation planning 24 The diversity-stability debate 25 The Medicago genome provides insight into the evolution of rhizobial symbioses 26 Twenty-first-century warming of a large Antarctic ice-shelf cavity by a redirected coastal current 27 Will a Large Complex System be Stable
上海交通大学通识教育立项核心课程 课程名称: 生物技术与人类 课程编号: BI 906 姓名: 宋伟强 班级: F1202002 学号: 5120209048 专业: 机动 阅读与理解 题目编号 21 得分 序 号 阅读文章名称 1 A new hominin foot from Ethiopia shows multiple Pliocene bipedal adaptations 2 Additive threats from pathogens, climate and land-use change for global amphibian diversity 3 Causes, consequences and ethics 4 Changing Arctic Ocean freshwater pathways 5 Clonal evolution in relapsed acute myeloid leukaemia revealed by whole-genome sequencing 6 Comparing the yields of organic and conventional agriculture 7 Consequences of changing 8 Ecology drives a global network of gene exchange connecting the human microbiome 9 Emerging fungal threats to animal,plant and ecosystem health 10 Evolution of increased complexity in a molecular machine 11 Genetic contribution to stability and change in intelligence from childhood to old age 12 Getting the measure of biodiversity 13 Global patterns in biodiversity 14 Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation 15 Insights into hominid evolution from the gorilla genome sequence 16 Prediction mutation outcome from early stochastic variation in genetic interaction partners 17 Rapid evolutionary divergence and ecotypic diversification of germination behavior in weedy rice populations 18 Recent contribution of glaciers and ice caps to sea level rise 19 Regeneration of whole fertile plants from 30000-y-old fruit tissue buried in Siberian permafrost 20 Reversal of cocaine-evoked synaptic potentiation resets drug-induced adaptive behaviour 21 Stability and complexity in model ecosystems 22 Stability criteria for complex ecosystems 23 Systematic conservation planning 24 The diversity–stability debate 25 The Medicago genome provides insight into the evolution of rhizobial symbioses 26 Twenty-first-century warming of a large Antarctic ice-shelf cavity by a redirected coastal current 27 Will a Large Complex System be Stable

Sebastian Bonhoeffer Stability and complexity in model ecosystems.Nature.2011.3 模拟生态系统的稳定性和多样性 宋伟强 一,背景知识: 20世纪70年代以前,生态学家企图发展一种联系稳定性和多样性的通用理论。起初,0dum、 MacArthur、Elton等人提出稳定性随物种多样性的增加而提高的理论,然而Gardner、Ashby、 My向这个理论提出了挑战,认为较高的物种多样性并不意味着较稳定的生态系统,并且用了 一定的实验验证自己的理论。 20世纪20年代,美国的数学家Lotka导出有关寄主与寄生者之间数量关系的著名数学模 型:1926年意大利数学家Volterra提出了捕食者与被捕食者的模型,因Lotka与Volterra 分别提出种间竞争的模型,因而通常称之为Lotka--Volterra模型,种群数学生态学得到特别 迅速的发展。[1] 二.创新点: 作者在多物种Lotka-Volterra模型(multi-species LVM)的基础上运用R commander 的运行来模拟生态系统内各物种的相互影响,并由重复模拟实现科学性。创新性在于它提出 了一种新的模型来模拟生态系统的演变,并以此来验证理论思想,数学建模在生态学中得到 了应用。整个过程只需输入一个初始值就能得到结果,重复模拟就能得到大量数据,方法简 便,实验数据相对可靠。 三.读后感: 读完这篇文章之后,我深刻认识到了各个学科穿插的重要性,作者通过数学建模模拟生 态系统的演变,并通过R commander软件运行得到统计结果。那我就在这里讲下我读完文章 后对算法的一些理解: 首先是May对直线型的种族数量与生态系统间稳定性的关系提出了质疑,并成功的用数 学的方法模拟并证实了生态系统结构与稳定性的关系远远不止于正比的关系。但他的方法同 样有很多的限制,比如他专注于集合的随机地域,现实中的地域通常都不是随机的,另一方 面关于生物的灭亡,很显然稀有生物更容易被灭亡,因此这种模拟算法还不够完善。 鉴于May的模拟算法存在缺陷,作者Sebastian Bonhoeffer提出了一种新的模拟算法
Sebastian Bonhoeffer .Stability and complexity in model ecosystems.Nature.2011.3 模拟生态系统的稳定性和多样性 宋伟强 一.背景知识: 20世纪 70年代以前,生态学家企图发展一种联系稳定性和多样性的通用理论。起初,Odum、 MacArthur、Elton 等人提出稳定性随物种多样性的增加而提高的理论,然而 Gardner、Ashby、 May 向这个理论提出了挑战,认为较高的物种多样性并不意味着较稳定的生态系统,并且用了 一定的实验验证自己的理论。 20 世纪 20 年代,美国的数学家 Lotka 导出有关寄主与寄生者之间数量关系的著名数学模 型;1926 年意大利数学家 Volterra 提出了捕食者与被捕食者的模型,因 Lotka 与 Volterra 分别提出种间竞争的模型,因而通常称之为 Lotka-Volterra 模型,种群数学生态学得到特别 迅速的发展。[1] 二.创新点: 作者在多物种 Lotka-Volterra 模型(multi-species LVM)的基础上运用 R commander 的运行来模拟生态系统内各物种的相互影响,并由重复模拟实现科学性。创新性在于它提出 了一种新的模型来模拟生态系统的演变,并以此来验证理论思想,数学建模在生态学中得到 了应用。整个过程只需输入一个初始值就能得到结果,重复模拟就能得到大量数据,方法简 便,实验数据相对可靠。 三.读后感: 读完这篇文章之后,我深刻认识到了各个学科穿插的重要性,作者通过数学建模模拟生 态系统的演变,并通过 R commander 软件运行得到统计结果。那我就在这里讲下我读完文章 后对算法的一些理解: 首先是 May 对直线型的种族数量与生态系统间稳定性的关系提出了质疑,并成功的用数 学的方法模拟并证实了生态系统结构与稳定性的关系远远不止于正比的关系。但他的方法同 样有很多的限制,比如他专注于集合的随机地域,现实中的地域通常都不是随机的,另一方 面关于生物的灭亡,很显然稀有生物更容易被灭亡,因此这种模拟算法还不够完善。 鉴于 May 的模拟算法存在缺陷,作者 Sebastian Bonhoeffer 提出了一种新的模拟算法

这种算法大致如下: 文章使用数字模拟多物种的Lotka-Volterra模型来取样调查生态系统的稳定性如何与 生态系统的大小联系,并得出结论。而且默认在此模型中,2个种群中,种群1的内部物种竞 争是弱于不同种群间的竞争的。多种族的LVW模型中,我们设定每个族群的携带容量为1并 忽略一般性的损失.ij的大小在大于0以及大于1时会代表不同的含义。捕食者与被捕者 的关系也能被概括为aij大于0与小于0的反应。在此模型中,基于从简的原因,在此只讨 论竞争反应。 用aij表示物种j对物种i的作用,如果aij>0,则表示物种j阻碍物种i的发展, aii表示物种内部的自生作用,如果aij>1那么物种j对物种i的阻碍大于物种i对自 身的阻碍,且aij构成一个矩阵(对角线上的元素要保证大于0,否则这个种群将无限发展)。 再用后面的算法在R程序中算出结果(ni是物种密度,t是时间,ri是生长率): dni/dt =(ri- for i=1,....N 因此有了文章中这个算法之后,我们只要确定了初始的物种密度,生长率,物种之间的 影响,就能根据这个方程就能推算出物种密度关于时间的变化从而得到最后的结果。 以上就是整个算法的梗概,我大概了解了这么多,至于后面那些更加深奥的关于编程的 东西由于专业原因个人不是非常清楚,但也由此算法了解了大概思路。 此外,在阅读本文的过程中,我也查阅了许多资料,让我对生态系统的稳定性有了更深 的认识:原本受中学教学的影响,我一直坚定的认为一个生态系统中由于食物网的存在,物 种越多,生态系统的稳定性自然也就越强,但在查阅资料后才发现并不一定是如此,物种多 了以后生物系统内物种联结到一定程度后,系统即从稳定变得不稳定,等等。因此,生态系 统的稳定性与物种多样性的关系到现在都还是热点讨论话题,让我大长见识。 总的来说,这篇文章让我认识到了数学建模的魅力,生态学不能离开实验,但只知道埋 头做实验也会研究的效率低下,合理做到各个学科的穿插才能取得更令人满意的效果。 参考文献: [1]黄建辉,韩兴国.生物多样性和生态系统稳定性.CHINESE BIODIVERSITY..1995.3(1):3137
这种算法大致如下: 文章使用数字模拟多物种的 Lotka-Volterra 模型来取样调查生态系统的稳定性如何与 生态系统的大小联系,并得出结论。而且默认在此模型中,2 个种群中,种群 1 的内部物种竞 争是弱于不同种群间的竞争的。多种族的 LVM 模型中,我们设定每个族群的携带容量为 1 并 忽略一般性的损失. aij 的大小在大于 0 以及大于 1 时会代表不同的含义。 捕食者与被捕者 的关系也能被概括为 aij 大于 0 与小于 0 的反应。在此模型中,基于从简的原因,在此只讨 论竞争反应。 用 aij 表示物种 j 对物种 i 的作用,如果 aij > 0 ,则表示物种 j 阻碍物种 i 的发展, aii 表示物种内部的自生作用,如果 aij > 1 那么物种 j 对物种 i 的阻碍大于物种 i 对自 身的阻碍,且 aij 构成一个矩阵(对角线上的元素要保证大于 0,否则这个种群将无限发展)。 再用后面的算法在 R 程序中算出结果(ni 是物种密度,t 是时间,ri 是生长率): 因此有了文章中这个算法之后,我们只要确定了初始的物种密度,生长率,物种之间的 影响,就能根据这个方程就能推算出物种密度关于时间的变化从而得到最后的结果。 以上就是整个算法的梗概,我大概了解了这么多,至于后面那些更加深奥的关于编程的 东西由于专业原因个人不是非常清楚,但也由此算法了解了大概思路。 此外,在阅读本文的过程中,我也查阅了许多资料,让我对生态系统的稳定性有了更深 的认识:原本受中学教学的影响,我一直坚定的认为一个生态系统中由于食物网的存在,物 种越多,生态系统的稳定性自然也就越强,但在查阅资料后才发现并不一定是如此,物种多 了以后生物系统内物种联结到一定程度后,系统即从稳定变得不稳定,等等。因此,生态系 统的稳定性与物种多样性的关系到现在都还是热点讨论话题,让我大长见识。 总的来说,这篇文章让我认识到了数学建模的魅力,生态学不能离开实验,但只知道埋 头做实验也会研究的效率低下,合理做到各个学科的穿插才能取得更令人满意的效果。 参考文献: [1]黄建辉,韩兴国.生物多样性和生态系统稳定性.CHINESE BIODIVERSITY.1995.3(1);31~37