钢筋混凝土结构设计 设计指导书 一肋梁楼盖的计算简图 在进行内力分析前,必须先把楼盖实际结构抽象成为一个计算简图,在抽象过 程中要忽略一些次要因素,并做如下假定: 1.板的竖向荷载全部沿短跨方向传给次梁,且荷载→板→次梁→主梁→主 梁支承的传递过程中,支承条件简化为集中于一点的支承链杆,忽略支承构件的竖 向变形,即按简支考虑。 2.板视为以次梁为铰支座的连续梁,可取1m宽板带计算。 3.跨数超过5跨的等截面连续梁(板),当各跨荷载基本相同,且跨度相 差不超过10%时,可按5跨连续梁(板)计算,所有中间跨的内力和配筋均按第 三跨处理。当梁板实际跨数小于5跨时,按实际跨数计算。 4.板梁的计算跨度应取为相邻两支座反力作用点之间的距离,其值与支座 反力分布有关,也与构件的支承长度和构件本身的刚度有关。在实用计算中,计算 跨度可按表3取值。 表3 梁、板的计算跨度 10=l+a 两端搁置 且 1≤1+h(板)》 1≤1.051.(梁) 单跨 lo=l+a/2 弹 一端搁置、一端与支承构件 且 1a≤l.+h/2 (板) 性 整浇 1o≤1.0251 (梁) 理 两端与支承构件整浇 lo=l 论 1。ln+a/2+b/2 计 边跨 1≤1+h/24b/2(板) 16≤1.0251.+b/2(梁) 多跨 中间跨 1o=1. 且 1o≤1.11.(板) 1≤1.051.(梁) 按 10=l+a 塑 两端搁置 且 1≤1+h(板) 1。≤1.051n(梁) 理 1。l.+a/2 论 端搁置、 端与支承构件整浇 1o≤l+h/2(板) 1≤1.0251.(梁) 两端与支承构件整浇 1=1a 注:1。一板、梁的计算跨度: 1一支座中心线间距离: 1。一板、梁的净跨: 一板厚: a一板、梁端支承长度: b一中间支座宽度 二按弹性方法计算内力 按弹性理论计算的楼盖内力,首先要假定楼盖材料为均质弹性体。根据前述的
钢筋混凝土结构设计 设计指导书 一 肋梁楼盖的计算简图 在进行内力分析前,必须先把楼盖实际结构抽象成为一个计算简图,在抽象过 程中要忽略一些次要因素,并做如下假定: 1.板的竖向荷载全部沿短跨方向传给次梁,且荷载→板→次梁→主梁→主 梁支承的传递过程中,支承条件简化为集中于一点的支承链杆,忽略支承构件的竖 向变形,即按简支考虑。 2.板视为以次梁为铰支座的连续梁,可取 1m 宽板带计算。 3.跨数超过 5 跨的等截面连续梁(板),当各跨荷载基本相同,且跨度相 差不超过 10%时,可按 5 跨连续梁(板)计算,所有中间跨的内力和配筋均按第 三跨处理。当梁板实际跨数小于 5 跨时,按实际跨数计算。 4.板梁的计算跨度应取为相邻两支座反力作用点之间的距离,其值与支座 反力分布有关,也与构件的支承长度和构件本身的刚度有关。在实用计算中,计算 跨度可按表 3 取值。 表 3 梁、板的计算跨度 两端搁置 l0=ln+a 且 l0≤ln+h (板) l0≤1.05ln(梁) 一端搁置、一端与支承构件 整浇 l0=ln+a/2 且 l0≤ln+h/2 (板) l0≤1.025ln (梁) 单跨 两端与支承构件整浇 l0=ln 边跨 l0=ln+a/2+b/2 且 l0≤ln+h/2+b/2 (板) l0≤1.025ln+b/2 (梁) 按 弹 性 理 论 计 算 多跨 中间跨 l0=lc 且 l0≤1.1ln (板) l0≤1.05ln (梁) 两端搁置 l0=ln+a 且 l0≤ln+h (板) l0≤1.05ln (梁) 一端搁置、一端与支承构件整浇 l0=ln+a/2 且 l0≤ln+h/2 (板) l0≤1.025ln (梁) 按 塑 性 理 论 计 算 两端与支承构件整浇 l0=ln 注:l0—板、梁的计算跨度; lc—支座中心线间距离; ln—板、梁的净跨; h—板厚; a—板、梁端支承长度; b—中间支座宽度 二 按弹性方法计算内力 按弹性理论计算的楼盖内力,首先要假定楼盖材料为均质弹性体。根据前述的

计算简图,用结构力学的方法计算梁板内力,也可利用静力计算手册中的图表确定 梁、板内力。在计算内力时应注意下列问题: 1.荷载及其不利组合 楼蓝上作用有永久荷载和可变荷载,永久荷载按实际考虑,可变荷载根据统计 资料折算成等效均布活荷载,可由《建筑结构荷载规范》查得。板通常取1m板宽 的均布荷载(包括自重),次梁承受板传来的均布荷载和次梁自重,主梁承受次梁 传来得集中荷载和均布的自重荷载。为简化计算,可将主梁的自重按就近集中的原 则化为集中荷载,作用在集中荷载作用点和支座处(支座处的集中荷载在梁中不产 生内 由于可变荷载在各跨的分布是随机的,如何分布会在各截面产生最大内力是 活荷载不利布置的问题。 图2所示为5跨连续梁,当活荷载布置在不同跨间时梁的弯矩图及剪力图。 由图可见,当求1,3,5跨跨中最大正弯矩时,活荷应布置在1,3,5跨:当求2, 4跨跨中最大正弯矩或1, 活荷载应布置在2,4跨:当 此看出,活荷载在连续梁各跨满布时,并不是最不利情况。 (a (e) 图25跨连续梁弯矩图及剪力图
计算简图,用结构力学的方法计算梁板内力,也可利用静力计算手册中的图表确定 梁、板内力。在计算内力时应注意下列问题: 1.荷载及其不利组合 楼盖上作用有永久荷载和可变荷载,永久荷载按实际考虑,可变荷载根据统计 资料折算成等效均布活荷载,可由《建筑结构荷载规范》查得。板通常取 1m 板宽 的均布荷载(包括自重),次梁承受板传来的均布荷载和次梁自重,主梁承受次梁 传来得集中荷载和均布的自重荷载。为简化计算,可将主梁的自重按就近集中的原 则化为集中荷载,作用在集中荷载作用点和支座处(支座处的集中荷载在梁中不产 生内力)。 由于可变荷载在各跨的分布是随机的,如何分布会在各截面产生最大内力是 活荷载不利布置的问题。 图 2 所示为 5 跨连续梁,当活荷载布置在不同跨间时梁的弯矩图及剪力图。 由图可见,当求 1,3,5 跨跨中最大正弯矩时,活荷应布置在 1,3,5 跨;当求 2, 4 跨跨中最大正弯矩或 1,3,5 跨跨中最小弯矩时,活荷载应布置在 2,4 跨;当 求 B 支座最大负弯矩及支座最大剪力时,活荷载应布置在 1,2,4 跨,如图 3。由 此看出,活荷载在连续梁各跨满布时,并不是最不利情况。 图 2 5 跨连续梁弯矩图及剪力图

(a)(M,)(M).(M,)一的活荷袋布置 四为· (M)e,(M,a的活荷布置 (c)(Mn),(V)的话横教布爱 图3 活载不利位置 (a)活1+活3+活5 (b)活2+活4 (c)活1+活2+活4 从以上分析可得,确定截面最不利内力时,活荷载的布置原则如下: (1)欲求某跨跨中最大正弯矩时,除将活荷载布置在该跨以外,两边应每隔 一跨布置活载 (2)欲求某支座截面最大负弯矩时,除该支座两侧应布置活荷载外,两侧每 隔一跨还应布置活载: (3)欲求梁支座截面(左侧或右侧)最大剪力时,活荷载布置与求该截面最 大负弯矩时的布置相同: (4)欲求某跨跨中最小弯矩时,该跨应不布置活载,而在两相邻跨布置活载, 然后再每隔 一跨布置活载。 2.内力包络图 以恒载作用在各截面的内力为基础,在其上分别叠加对各截面最不利的活载布 置时的内力,便得到了各截面可能出现的最不利内力。 将各截面可能出现的最不利内力图叠绘于同一基线上,这张叠绘内力图的外包 线所形成的图称为内力包络图。它表示连续梁在各种荷载不利组合下, 各截面 产生的最不利内力。 无论活荷载如何分布,梁各截面的内力总不会超出包络图上的 内力值。梁截面可依据包络图提供的内力进行截面设计。图4为五跨连续梁的弯矩 包络图和剪力包络图。 、4 +g(124
图 3 活载不利位置 (a) 活 1+活 3+活 5 (b) 活 2+活 4 (c) 活 1+活 2+活 4 从以上分析可得,确定截面最不利内力时,活荷载的布置原则如下: (1)欲求某跨跨中最大正弯矩时,除将活荷载布置在该跨以外,两边应每隔 一跨布置活载; (2)欲求某支座截面最大负弯矩时,除该支座两侧应布置活荷载外,两侧每 隔一跨还应布置活载; (3)欲求梁支座截面(左侧或右侧)最大剪力时,活荷载布置与求该截面最 大负弯矩时的布置相同; (4)欲求某跨跨中最小弯矩时,该跨应不布置活载,而在两相邻跨布置活载, 然后再每隔一跨布置活载。 2.内力包络图 以恒载作用在各截面的内力为基础,在其上分别叠加对各截面最不利的活载布 置时的内力,便得到了各截面可能出现的最不利内力。 将各截面可能出现的最不利内力图叠绘于同一基线上,这张叠绘内力图的外包 线所形成的图称为内力包络图。它表示连续梁在各种荷载不利组合下,各截面可能 产生的最不利内力。无论活荷载如何分布,梁各截面的内力总不会超出包络图上的 内力值。梁截面可依据包络图提供的内力进行截面设计。图 4 为五跨连续梁的弯矩 包络图和剪力包络图
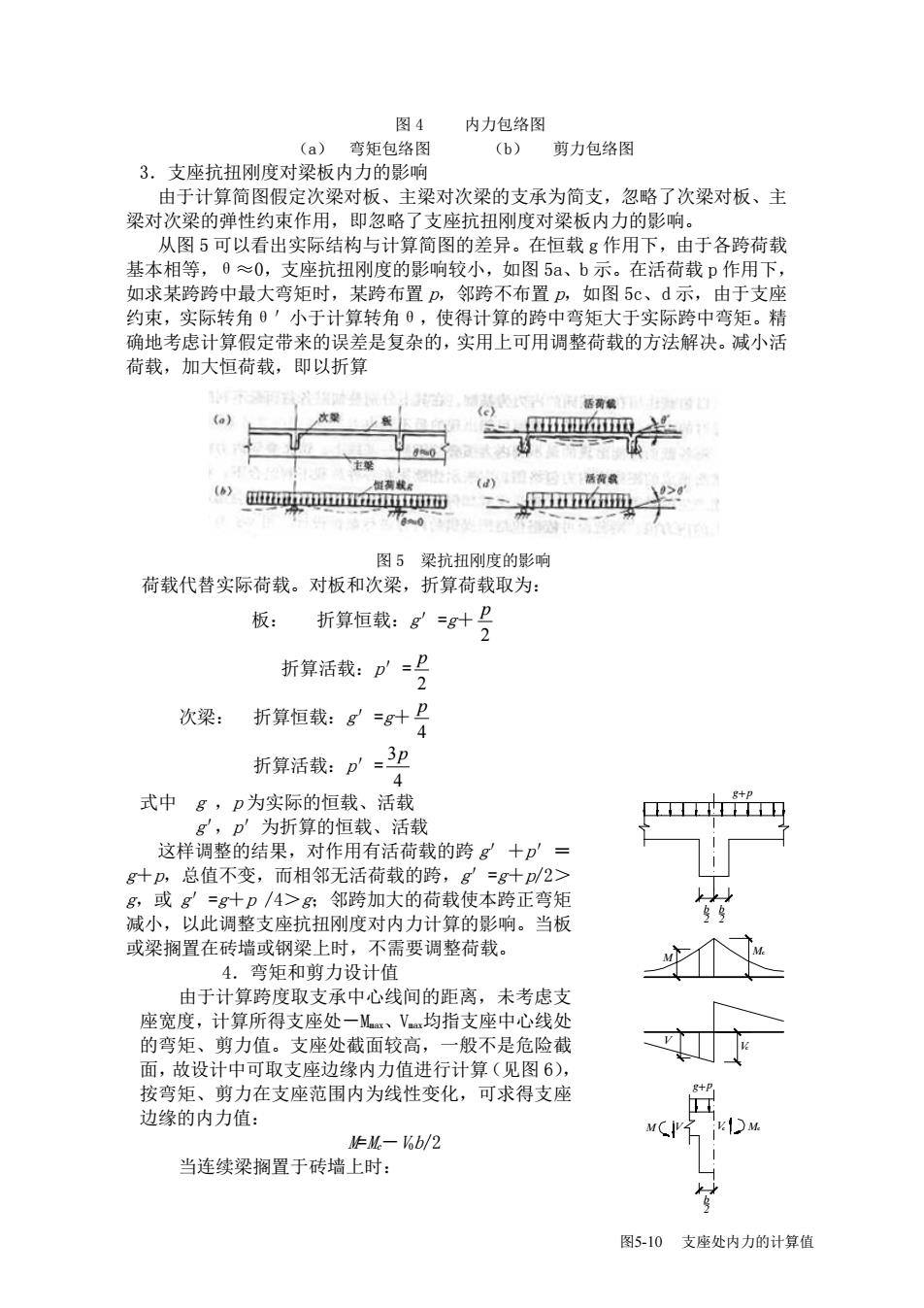
图4 内力包络图 (a)弯矩包络图 (b) 剪力包络图 3.支座抗扭刚度对梁板内力的影响 由于计算简图假定次梁对板、主梁对次梁的支承为简支,忽略了次梁对板、主 梁对次梁的弹性约束作用,即忽略了支座抗扭刚度对梁板内力的影响。 从图5可以看出实际结构与计算简图的差异。在恒载g作用下,由于各跨荷载 基本相等,0≈0,支座抗扭刚度的影响较小,如图5a、b示。在活荷载p作用下, 如求某跨跨中最大弯矩时,某跨布置 邻跨不布置p,如图5 d示,由千古成 实际转 角0'小于计算转角 使得计算的跨 中弯矩大于 实际跨中弯矩。精 确地考虑计算假定带来的误差是复杂的,实用上可用调整荷载的方法解决。减小活 荷载,加大恒荷载,即以折算 回桥荷线 》m品 一m半 图5梁抗扭刚度的影响 荷载代替实际荷载。对板和次梁,折算荷载取为: 板: 折算恒载:8=8+号 折算活载:p=号 次梁:折算恒载:g=g十 折算活载:p=3卫 4 式中g,p为实际的恒载、活载 D为折算的恒载、活载 卫 这样调整 结果 对作用有活荷载的跨g十pD g十P,总值不变,而相邻无活荷载的跨,g=g十p2> g,或g=g十p/4>邻跨加大的荷载使本跨正弯矩 减小,以此调整支座抗扭刚度对内力计算的影响。当板 或梁搁置在砖墙或钢梁上时,不需要调整荷载。 弯矩和剪力设计值 个 由于计算跨度取支承中心线间的距离,未考虑支 座宽度,计算所得支座处一Mr、V均指支座中心线处 的弯矩、剪力值。支座处截面较高,一般不是危险截 面,故设计中可取支座边缘内力值进行计算(见图6), 按弯矩、 剪力在支座范围内为线性变化, 可求得支座 边缘的内力值: 片M一6b/2 当连续梁搁置于砖墙上时: 图5-10支座处内力的计算值
图 4 内力包络图 (a) 弯矩包络图 (b) 剪力包络图 3.支座抗扭刚度对梁板内力的影响 由于计算简图假定次梁对板、主梁对次梁的支承为简支,忽略了次梁对板、主 梁对次梁的弹性约束作用,即忽略了支座抗扭刚度对梁板内力的影响。 从图 5 可以看出实际结构与计算简图的差异。在恒载 g 作用下,由于各跨荷载 基本相等,θ≈0,支座抗扭刚度的影响较小,如图 5a、b 示。在活荷载 p 作用下, 如求某跨跨中最大弯矩时,某跨布置 p,邻跨不布置 p,如图 5c、d 示,由于支座 约束,实际转角θ'小于计算转角θ,使得计算的跨中弯矩大于实际跨中弯矩。精 确地考虑计算假定带来的误差是复杂的,实用上可用调整荷载的方法解决。减小活 荷载,加大恒荷载,即以折算 图 5 梁抗扭刚度的影响 荷载代替实际荷载。对板和次梁,折算荷载取为: 2 p 板: 折算恒载:g'=g+ 2 p 折算活载:p'= 4 p 次梁: 折算恒载:g'=g+ 4 3p 折算活载:p'= 式中 g ,p 为实际的恒载、活载 g',p'为折算的恒载、活载 这样调整的结果,对作用有活荷载的跨 g'+p'= g+p,总值不变,而相邻无活荷载的跨,g'=g+p/2> g,或 g'=g+p /4>g;邻跨加大的荷载使本跨正弯矩 减小,以此调整支座抗扭刚度对内力计算的影响。当板 或梁搁置在砖墙或钢梁上时,不需要调整荷载。 4.弯矩和剪力设计值 由于计算跨度取支承中心线间的距离,未考虑支 座宽度,计算所得支座处-Mmax、Vmax均指支座中心线处 的弯矩、剪力值。支座处截面较高,一般不是危险截 面,故设计中可取支座边缘内力值进行计算(见图 6), 按弯矩、剪力在支座范围内为线性变化,可求得支座 边缘的内力值: M=Mc-V0b/2 当连续梁搁置于砖墙上时: Mc M M V V M 图5-10 支座处内力的计算值 b 2 c c + V g p Vc b 2 b 2 g+p

长 均布荷载: =-(g+g)b/2 集中荷载 6 式中,一支承中的弯矩、剪力值: (一按简支梁计算的支座剪力设计值(取绝对值): b一支承宽度。 三按塑性内力重分布的方法计算内力 钢筋混凝 是 种弹塑性材料,连续梁板是超静定结构,当梁板的 一个截面 达到极限承载力时,并不意味着整个结构的破坏。钢筋达到屈服后,还会产生一定 的塑性变形,结构的实际承载能力通常大于按弹性理论计算的结果。再则,混凝土 构件截面设计时,考虑了材料的塑性,若内力分析按弹性理论,与截面设计的理论 不统 因此有必要研究塑性理论的内力分析方法。 连续 考虑塑性内力重分布的计算方法较多,例如:极限平衡法、塑性铰 法及弯矩调幅法等。目前工程上应用较多的是弯矩调幅法。 弯矩调幅法的概念是:先按弹性分析求出结构各截面弯矩值,再根据需要将 结构中一些截面的最大(绝对值)弯矩(多数为支座弯矩)予以调整,按调整后的 内力进行截面配筋设 (1)弯关 法简称调幅法,调幅的基本原则是 1)为尽可能节约钢材,宜使用调整后的弯矩包络图做为设计配筋依据。 2)为方便施工,通常调整支座截面,并尽可能使调整后的支座弯矩与跨中弯矩 接近。 3)调辐需使结构满足则府、裂隆要求,不使支座截面讨早出现潮性较,调幅值 般≤25%。调幅后,所有支座及跨中弯矩的绝对值,当承受均布荷载时应满 足 24(8+g) 当p/g≤1/3时,调幅值≤15%,这是考虑长期荷载对结构变形的不利影响。 4)调幅后应满足静力平衡条件,即调整后的每跨两端支座弯矩平均值与跨中 弯矩之和(均为绝对值),不小 于该跨满载时(恒+活)按简支梁计算的跨中弯矩 (见图7)。 M,+M五十≥品 M IHHIimmiHnin M 12
M=Mc 均布荷载: =Vc-(g+q)b/2 集中荷载: 6 Vc=V 式中 Mc、Vc-支承中的弯矩、剪力值; V0—按简支梁计算的支座剪力设计值(取绝对值); b-支承宽度。 三 按塑性内力重分布的方法计算内力 钢筋混凝土是一种弹塑性材料,连续梁板是超静定结构,当梁板的一个截面 达到极限承载力时,并不意味着整个结构的破坏。钢筋达到屈服后,还会产生一定 的塑性变形,结构的实际承载能力通常大于按弹性理论计算的结果。再则,混凝土 构件截面设计时,考虑了材料的塑性,若内力分析按弹性理论,与截面设计的理论 不统一,因此有必要研究塑性理论的内力分析方法。 连续梁板考虑塑性内力重分布的计算方法较多,例如:极限平衡法、塑性铰 法及弯矩调幅法等。目前工程上应用较多的是弯矩调幅法。 弯矩调幅法的概念是:先按弹性分析求出结构各截面弯矩值,再根据需要将 结构中一些截面的最大(绝对值)弯矩(多数为支座弯矩)予以调整,按调整后的 内力进行截面配筋设计。 (1)弯矩调幅法简称调幅法,调幅的基本原则是: 1)为尽可能节约钢材,宜使用调整后的弯矩包络图做为设计配筋依据。 2)为方便施工,通常调整支座截面,并尽可能使调整后的支座弯矩与跨中弯矩 接近。 3)调幅需使结构满足刚度、裂缝要求,不使支座截面过早出现塑性铰,调幅值 一般≤25%。调幅后,所有支座及跨中弯矩的绝对值 M,当承受均布荷载时应满 足: M≥ 24 1 (g+q)l 2 当 p/g≤1 /3 时,调幅值≤15%,这是考虑长期荷载对结构变形的不利影响。 4) 调幅后应满足静力平衡条件,即调整后的每跨两端支座弯矩平均值与跨中 弯矩之和(均为绝对值),不小于该跨满载时(恒+活)按简支梁计算的跨中弯矩M0 (见图 7)。 2 + MM BA +MC≥M0

图7M示意图 5)为保证塑性铰具有足够的转动能力,设计中应满足£≤0.35,钢筋宜使用 HRB335级和HRB400级热轧钢筋,也可采用HPB235级热轧钢筋,宜选用C20~C45 强度等级混凝 6)考虑塑性内力重分布后,抗剪箍筋面积增大20%,增大范围1见图8。 为避免斜拉破坏,配筋下限值应满足: L工▣(6) 1到 图8 抗剪箍筋增大范围示意图 (a)集中荷载 (b) 均布荷载作用 (2)用弯矩调幅法计算等跨连续梁板 根据调幅法的原则,并考虑到设计的方便,对均布荷载作用下的等跨连续梁 板,考虑塑性内力重分布后的弯矩和剪力的计算公式为: 作a(g+p)6 =B(g+p)1 式中,a,B一弯矩和剪力系数,分别见表4,表5 。,1。一计算跨度和净 BP一均布恒载和活载的设计值 梁板弯矩系数。 表4 截面 支承条件 梁 板 梁、板搁置在墙上 0 0 边支座 梁、板与梁整浇 -1/24 -1/16 梁与柱整浇 -1/16 梁、板搁置在墙上 1/11 边跨中 梁、板与梁整浇 1/14 第一内支座 两跨连续 -1/10 三跨及三跨以上连续 -1/11 中间支座 -1/16 中间跨中 1/16
图 7 M0 示意图 5)为保证塑性铰具有足够的转动能力,设计中应满足ξ≤0.35,钢筋宜使用 HRB335 级和 HRB400 级热轧钢筋,也可采用 HPB235 级热轧钢筋,宜选用 C20~C45 强度等级混凝土。 6) 考虑塑性内力重分布后,抗剪箍筋面积增大 20%,增大范围 l 见图 8。 为避免斜拉破坏,配筋下限值应满足: yv C f 03.0 f bs ASV ρsv = > 图 8 抗剪箍筋增大范围示意图 (a)集中荷载作用 (b) 均布荷载作用 (2)用弯矩调幅法计算等跨连续梁板 根据调幅法的原则,并考虑到设计的方便,对均布荷载作用下的等跨连续梁 板,考虑塑性内力重分布后的弯矩和剪力的计算公式为: M=α(g+p)l2 0 V=β(g+p)l2 n 式中,α,β—弯矩和剪力系数,分别见表 4,表 5 l0,ln—计算跨度和净跨 g,p—均布恒载和活载的设计值 梁板弯矩系数α 表 4 截面 支承条件 梁 板 梁、板搁置在墙上 0 0 梁、板与梁整浇 -1/24 -1/16 边支座 梁与柱整浇 -1/16 梁、板搁置在墙上 1/11 边跨中 梁、板与梁整浇 1/14 两跨连续 -1/10 第一内支座 三跨及三跨以上连续 -1/11 中间支座 -1/16 中间跨中 1/16

梁剪力系数B 表5 截面 支承条件 端支座内侧 搁置在墙上 0.45 与泌成柱整淡 0.5 第一支内座外测 搁置在墙上 0.6 与梁或柱整浇 0.55 第一支内座内测 0.55 中间支座两侧 0.55 以图9示,5跨等跨连续梁承受均布荷载为例,用调幅法阐明上述系数由来。 次梁边支座为砖墙, 设活荷载与恒荷载之比p/ 6=3,1为跨度 口g□ DgD 0 T四 图9五跨连续梁荷载布置图 (a)五等跨连续梁(b)求M时荷载布置图 (c)求1、3、5跨中最大弯矩时荷载布置图 即 F3g /3 匹号智 8时Fg+3g=4g 于是 p=3(g+p) 8=(g+p) 次梁折算荷载 g=g+是-g+p小+日g+p-n.485(erp p)-0.625() 按弹性方法求,活载布置在一、二、四跨(如图9),由附表可查得横 荷载系数-0.105,活荷载系数-0.119,则 6=-0.105gP-0.119pP -0.105×0.4375(g+p)-0.119×0.5625(g+p)f =-0.1129(g*p)f
梁剪力系数β 表 5 截面 支承条件 梁 搁置在墙上 0.45 端支座内侧 与梁或柱整浇 0.5 搁置在墙上 0.6 第一支内座外测 与梁或柱整浇 0.55 第一支内座内测 0.55 中间支座两侧 0.55 以图 9 示,5 跨等跨连续梁承受均布荷载为例,用调幅法阐明上述系数由来。 次梁边支座为砖墙,设活荷载与恒荷载之比 p / g=3,l 为跨度。 图 9 五跨连续梁荷载布置图 (a) 五等跨连续梁 (b)求MBmax时荷载布置图 (c)求 1、3、5 跨中最大弯矩时荷载布置图 (c) (b) p' g ' p' p' g ' p' (a) p' 即 p=3g g=p/3 3 p 3 4 p 则 g+p= +p= g+p= +3 g g =4 g ( ) += pgp 4 3 于是 ( ) += pgg 4 1 4 p g + ( ) 4 1 4 1 pg ++ ( +⋅ pg 4 3 次梁折算荷载 g'= = )=0.4375(g+p) 4 3p 4 3 ( +⋅ pg 4 3 p'= = )=0.5625(g+p) 按弹性方法求MBmax,活载布置在一、二、四跨(如图 9),由附表可查得横 荷载系数-0.105,活荷载系数-0.119,则 MBmax= -0.105 g'l 2 -0.119 p'l 2 =-0.105×0.4375(g+p)l 2 -0.119×0.5625(g+p)l 2 =-0.1129(g+p)l 2

考虑调幅值20%(≤25%),则 0.8k=-0.0903(gp)07(gp)f *i(g*p)-0.0909(gp)f 取=0.0909(g+D)F,按静力平衡条件,可求得边跨间任意处弯矩,取B 跨为隔离体,见图10。 +p8+P+ 四。 R 6 w 图10边跨跨中最大弯矩示意 由∑M8=0 i(g*p)f+R1-2(g*p)f=0 得 R=0.4091(g*p)1 由∑y=0 R(gp)1-0.4091(g+p)1=0.5905(g+p)1 得 M=Ra1-2 (g+p)af 求跨间最大弯矩M的位置: 影0 RI(g+p)ap a=0.4091 k=Ra1-7(gp)ar-0.4091(g*p)f-2(gp)F(0.4091) =0.08368(g+p) 按弹性方法求M,活载布置在一、三、五跨(如图9C),由附表可查得横 荷载系数0.078,活荷载系数0.100,则 M'1=0.078 +0.100f =0.078×0.4375(g*p)+0.100×0.5625(g*p) =0.09037(g+p)f>M 1 应取用'的值,a=0.09037,即1106,为计算方便,取为i: (3)不等跨连续梁板的计算 当不等跨连续梁板的跨度差不大于10%时,仍可采用等跨连续梁板的系数。 计算支座弯矩时,取相邻两跨中的较大跨度值:计算跨中弯矩时,取本跨跨度 值
考虑调幅值 20%(≤25%),则 07.11 1 MB=0.8 MBmax=-0.0903(g+p)l 2 = (g+p)l 2 11 1 ≈ (g+p)l 2 =0.0909(g+p)l 2 取MB=0.0909(g+p)l 2 ,按静力平衡条件,可求得边跨间任意处弯矩,取AB 跨为隔离体,见图 10。 由∑ B =0 M 11 1 (g+p)l 2 +RAl- 2 1 (g+p)l 2 =0 得 RA=0.4091(g+p)l 图 由∑ y =0 RB=(g+p)l-0.4091(g+p)l=0.5905(g+p)l 得 M1= RAαl- 2 1 (g+p)α2 l 2 求跨间最大弯矩M1max的位置: 0 1 = ∂ ∂ α M RAl=(g+p)αl2 α=0.4091 M1max= RAαl- 2 1 (g+p)α2 l 2 =0.4091(g+p)l 2 — 2 1 (g+p)l 2 (0.4091)2 =0.08368(g+p)l 2 按弹性方法求M1max,活载布置在一、三、五跨(如图 9c),由附表] 可查得横 荷载系数 0.078,活荷载系数 0.100,则 M'1max=0.078g'l 2 +0.100p'l 2 =0.078×0.4375(g+p)l 2 +0.100×0.5625(g+p)l 2 =0.09037(g+p)l 2 >M1max 应取用M'1max的值,α=0.09037,即 06.11 1 ,为计算方便,取为11 1 。 (3)不等跨连续梁板的计算 当不等跨连续梁板的跨度差不大于 10%时,仍可采用等跨连续梁板的系数。 计算支座弯矩时,l0取相邻两跨中的较大跨度值;计算跨中弯矩时,l0取本跨跨度 值。 5-19 边跨跨中最大弯矩示意 αl R A M1 MB RB = + g+p l g+p g ' 1 11 A p ' - ( )l B 10

当不等跨连续梁板的跨度差大于10%时,连续梁应根据弹性方法求出恒载及活 荷载最不利作用的弯矩图,经组合叠加后形成弯矩包络图,再以包络图作为调幅依 据,按前述调幅原则调幅。剪力可取弹性方法的计算结果,连续板可按下述步骤计 算: 1)确定最大跨跨内弯矩值 边跨:g+p≥eg+p 11 14 中间跨:g+p≥eg+p 16 18 2)按已知最大跨跨中弯矩,在本跨(g十p)作用下,由静力平衡条件求该跨 支座弯矩,再以支座弯矩为已知,同理求得邻跨跨中弯矩,以此类推,求得所有跨 中及支座弯矩,该弯矩均应符合内力平衡条件及大于2江(8叶))F (4)塑性内力重分布方法的适用范围 考虑塑性内力重分布的方法与弹性理论计算结果相比,节约材料,方便施工, 但在结构正常使用时,变形及裂缝偏大,对下列情况不适合采用塑性内力重分布的 计算方法, 承受动力荷载的结构构件:使用阶段不允许开裂的结构构件:轻质混凝土及其 它特种混凝土结构:受侵蚀气体或液体作用的结构:预应力结构和二次受力迭合结 构:主梁等重要构件不宜采用。 四截面设计及构造要求 确定了连续梁板的内力后,可根据内力进行构件的截面设计 一般情况下,强 度计算后再满足 定的构造要求, 可不进行变形 及裂缝宽度的验 梁板均为受弯构件,作为单个构件的计算及构造己在第三章中述及,此处仅对 受弯构件在楼盖结构中的设计和构造特点简要叙述。 1.板的计算及构造特点 (1)古承在次梁或砖墙上的连续板 ,一般可按塑性内力重分布的方法计算 9 板 一般均能满足斜截 面抗剪 设计时可 不进行打 剪计算 (3)在承载能力极限状态时,板支座处在负弯矩作用下上部开裂,跨中在 正弯矩的作用下部开裂,板的实际轴线成为一个拱形(图11)。当板的四周与梁 整浇,梁具有足够的刚度,使板的支座不能自由移动时,板在竖向荷载作用下将 产生水平推力,由此产生的支座反力对板产生的弯矩可抵消部分荷载作用下的弯 矩。因此对四周与梁整体连接的单向板,中间跨的跨中截面及中间支座,计算弯 矩可诚少20%,其它截面不予降低。 图11 板的拱作用 (4)板的受力钢筋的配置方法有弯起式和分离式两种,钢筋弯起切断位置见 图12,图中当p/g≤3时,a=l/4:当p/g>3时,a=l./3.1为板的净跨。弯起式可
当不等跨连续梁板的跨度差大于 10%时,连续梁应根据弹性方法求出恒载及活 荷载最不利作用的弯矩图,经组合叠加后形成弯矩包络图,再以包络图作为调幅依 据,按前述调幅原则调幅。剪力可取弹性方法的计算结果,连续板可按下述步骤计 算: 1) 确定最大跨跨内弯矩值 11 )( 2 + lpg 14 )( 2 + lpg 边 跨: ≥M≥ 16 )( 2 + lpg 18 )( 2 + lpg 中间跨: ≥M≥ 2)按已知最大跨跨中弯矩,在本跨(g+p)作用下,由静力平衡条件求该跨 支座弯矩,再以支座弯矩为已知,同理求得邻跨跨中弯矩,以此类推,求得所有跨 中及支座弯矩,该弯矩均应符合内力平衡条件及大于 24 1 (g+p)l 2 。 (4) 塑性内力重分布方法的适用范围 考虑塑性内力重分布的方法与弹性理论计算结果相比,节约材料,方便施工, 但在结构正常使用时,变形及裂缝偏大,对下列情况不适合采用塑性内力重分布的 计算方法: 承受动力荷载的结构构件;使用阶段不允许开裂的结构构件;轻质混凝土及其 它特种混凝土结构;受侵蚀气体或液体作用的结构;预应力结构和二次受力迭合结 构;主梁等重要构件不宜采用。 四 截面设计及构造要求 确定了连续梁板的内力后,可根据内力进行构件的截面设计。一般情况下,强 度计算后再满足一定的构造要求,可不进行变形及裂缝宽度的验算。 梁板均为受弯构件,作为单个构件的计算及构造已在第三章中述及,此处仅对 受弯构件在楼盖结构中的设计和构造特点简要叙述。 1.板的计算及构造特点 (1) 支承在次梁或砖墙上的连续板,一般可按塑性内力重分布的方法计算。 (2) 板一般均能满足斜截面抗剪要求,设计时可不进行抗剪计算。 (3) 在承载能力极限状态时,板支座处在负弯矩作用下上部开裂,跨中在 正弯矩的作用下部开裂,板的实际轴线成为一个拱形(图 11)。当板的四周与梁 整浇,梁具有足够的刚度,使板的支座不能自由移动时,板在竖向荷载作用下将 产生水平推力,由此产生的支座反力对板产生的弯矩可抵消部分荷载作用下的弯 矩。因此对四周与梁整体连接的单向板,中间跨的跨中截面及中间支座,计算弯 矩可减少 20%,其它截面不予降低。 图 11 板的拱作用 (4) 板的受力钢筋的配置方法有弯起式和分离式两种,钢筋弯起切断位置见 图 12,图中当p/g≤3 时,a=ln/4;当p/g>3 时,a=ln/3。ln为板的净跨。弯起式可

一端弯起(图12())或两端弯起(图12(b)。弯起式配筋整体性好,节约钢材, 但施工复杂:分离式配筋(图12(c)施工方便,但用钢量稍大。 a10 脑的脑时 >完全葡支可不用 图12 板中受力钢筋的布置 (5)板除配置受力钢筋外,还应在与受力钢筋垂直的方向布置分布钢筋,分 布钢筋的作用是固定受力钢筋的位置:抵抗板内温度应力和混凝土收缩应力:承担 并分布板上局部荷载产生的内力:在四边支承板中,板的长方向产生少量弯矩也由 分布钢筋承受。分布钢筋的数量应不少于受力钢筋的10%,且每米不少于3根, 应均匀布置于受力钢筋的内侧。 由于计算简图与实际结构的差异,板嵌固在砖墙上时,支座处有一定负弯矩 板角处也有负弯矩,温度、混凝土收缩、施工条件等因素也会在板中产生拉应力。 为防止上述原因在板中产生裂缝,沿墙长每米配56构造钢筋,伸出墙边长度≥ 1/7。在角部/4范围内双向配6@200的负筋,伸出长度≥1/4。板靠近主梁 处,部分荷载直接传给主梁,也产生一定的负弯矩,同理应配置每米56钢筋, 伸出长度≥/4,板的构造钢筋配置见图13
一端弯起(图 12(a))或两端弯起(图 12(b))。弯起式配筋整体性好,节约钢材, 但施工复杂;分离式配筋(图 12(c))施工方便,但用钢量稍大。 图 12 板中受力钢筋的布置 (5)板除配置受力钢筋外,还应在与受力钢筋垂直的方向布置分布钢筋,分 布钢筋的作用是固定受力钢筋的位置;抵抗板内温度应力和混凝土收缩应力;承担 并分布板上局部荷载产生的内力;在四边支承板中,板的长方向产生少量弯矩也由 分布钢筋承受。分布钢筋的数量应不少于受力钢筋的 10%,且每米不少于 3 根, 应均匀布置于受力钢筋的内侧。 由于计算简图与实际结构的差异,板嵌固在砖墙上时,支座处有一定负弯矩, 板角处也有负弯矩,温度、混凝土收缩、施工条件等因素也会在板中产生拉应力。 为防止上述原因在板中产生裂缝,沿墙长每米配 5φ6 构造钢筋,伸出墙边长度≥ l0/7。在角部l0 / 4 范围内双向配φ6@ 200 的负筋,伸出长度≥l0/4。板靠近主梁 处,部分荷载直接传给主梁,也产生一定的负弯矩,同理应配置每米 5φ6 钢筋, 伸出长度≥l0/4,板的构造钢筋配置见图 13