
四川建筑科学研究 12 n Building Seie 荷载标准值与分项系数的分析 思小标,纪鹏元,曾兵 (中国建筑科学研究院,北京100013 摘要:近些年来我国时常出现建筑物被风吹毁,结构被雪压塌事故。针对于这些现象,本文对规范中风荷段,雪 荷载以及楼面均布荷载的标准值和分项系数的取值展开了分析。做了对荷规范相关内容的变动的分析,以及利 实测数据的计算结果的对比。分析结果表明,目前我国规范中的风荷载和雪荷载的取值偏低,分项系数的取值并 没有因地区不同面加以区别,不符合可靠性设计的基本原则,同时取值偏小。对于楼面均布荷载并没有按照规 中所规定的方 中图分类号:TU312,1 文献标志码:A 文章编号:1008-1933(2017)01-012-04 Analysis of load characteristics value and partial coefficient DI Xiaotan.JI Pengvuan,ZENG Bing (China Academy of Buildine Re arch.Beiiine 100013.China) Abstract:In recent years.a lot of buildings bave been destroved by wind and s in China.To find the reason this article analysed the content of the load,and c npared with the calculated results with the measured data.Analvsis results show that the characteristics value of wind load and snow load value is low,the pr ent standard of subentry coefficient value cannot meet the target reliability index.The alue of the partial coefficient is not different a cording to differer emake the reliability indexf rm live load does not follow the methods s cifed in the 0前言 1风荷载 目前我国的荷载规范是从《荷载暂行规范》(结 1.1风荷找的标准值 规-1一58而)逐渐发展而来。在发展的过程中鞋 我国《建筑结构指找规范》(GB50009一2012) 入了可靠度理论,逐渐发展成为目前现行规范中的 中规定:风速取 般平坦空旷地区(规范中的B 分项系数设计法 其中,基于可靠度理论分配给 类地貌),离地10m处的10min时距,重现期为50 载规范的分项系数与《荷载暂行规范》的超载系数 年的(年超越概率为0.02)的平均风速。在这里我 关联度极高,未按统一的可靠指标分析确定,通比 国的风速是取的10mn内的平均风速,这种取法必 较后确认,荷载标准值的概念源于《荷栽暂行规范》 将大大地低估标准风速值的大小 的标准荷载。同时基于实测数据分析,认为目前的 根据掌握的澳门地区风速资料,气象台站是按 标准值与分项系数并不能满足现行规范中所规定的 “小时”记录风速。每小时记录两个风速值,一个是 目标可靠度。本文将对风荷载,雪荷载以及楼面均 这一小时的最大3阵风风速,另一个是这一小时 布荷载进行分析。 的平均风速。就澳门地区的风速资料计算最大3。 阵风风速与60min平均风速比值,其比值并不周 定,具有较大的离散性。不同风速下的离散度最大 最小比值为1.2,最大比值接近2.5,相比较风速高 膜中国效科学研究院院应用技术所克课题 的时候,比值要小,在美国规范Minimum Design 作者简介:部小坛(1953-),男,顾士,研究员,主要从事结构理论研 Loads for Buildings and other structures (AScE/SEI 7. 10)同中给出了基于美国地区类标准地貌下测得的 E-mal:dixiacan@163.com 大量风速数据统计得到的风速时距的换算关系曲

2017a1 即小坛,等:荷我标准值与分项系数的分析 13 线,见图1。此时,3s阵风风速是10mim平均风速 0.98带入后文中的式(1)可求得表2中50年超越 的1.4倍,风压关系为1.96倍。 在我国规范中给出 概率0.02的荷载值 了阵风系数,但要小于实际的风压比值。 表2风速和风压的分项系数比较 Table 2 Comparison of the partial coefficient of wind speed and wind pressure 萄截值 统计参数 且a=2.59 11 由表2的x。m/x知可以得到分项系数yam,将风 速分项系数平方可以得到风压的分项系数v 10 由表2可以看到,无论是按风压还是风速计算 时地 的分项系数y…都远大于1.4,而且都具有地区性的 图!不同时距下风速值与一小时平均风速的比值 特点。按照风压确定的统一的分项系数1.4不仅偏 Fig.I Maximum speed averaged over t(s) 小,而且确实不符合可靠度理论。这里需要提示的 to hourly mean speed 是x。 1.2风荷载的分项系数 1型概率分布50年超越概率0.02 对于风荷载的取值都是基于风速的概率分布 的特征值对应的可靠指标为2.59。为了便于比较 而非风压。因此,分项系数似乎也应该以风速为基 将50年超越概率0.1、0.07,0.04对应的分项系数 准计算确定 。实际上,在很长一段时间内国内外 荷载值和可靠指标B。列于表3之中 用控制可靠指标或失效概率方法的荷载规范都存在 表3超越概率可常指标与分项系数等的比拟 者同样的问题,没有找对为风荷载设置分项系数的 Table 3 Comparison of reliability index,partial 对象和基准。美国规范在最新一版的规范中进行了 and beyond probability 修正,取消掉风荷载的分项系数,采用直接给出50 20 名称 年超越概率分别为0.15,0.07和10.03的风速作 5 设计值的方法。表1对3种典型情况的风速和风压 30.021:37 的统计参数进行了计算分析。 表】风速和风压的统计参数 由表3可以看到,极值1型分布50年超越概率 Table】Statistical pa ters of wind speed 0.1和0.04对应的可靠指标Ba1Bam分别为 nd wind pressure 1.30和2.04。 名称 荷载值 统计黎数 最后,再来看可靠度理论风荷载1,4的分项系 数和0.193(规范中所给出的风荷载变异系数)的变 异系数:按照B、=2.05和 =0.193计算 1.40。这是一种巧合吗?不过这种巧合来得太晚 表1中,风速之后对应的数值为海拔高度,风 了,而且这一数值既不适用丁风速也不适用丁风压 速表明对应风压x。=0.2和x=03的风速 风速1,4的分项系数平方后为风压的分项系数,该 17.94和21.97的海拔高度为55m。从表1可以看 值应为1.96,与表3中B。=2.04的系数相当 到,无论是统计数据极值【型分布的众值“还是纷 也就是说,目前的分项系数 .4至少要再放大1.4 计数据的均值以,无论是风速还是风压,都小于x 倍,才能满足B、=2.05对风压的要求 对应的数值。这与雪荷载的情况类似。表1中的 x知应该是荷载规范确定的风荷载的“标准值”,也是 2雪荷载 极值1型分布累积密度0.98分位的特征值。 2.1雪荷载的标准馆 为了估算其分项系数,将表1中的用 荷载规范认定基本雪压统计数据符合极值I型 代,将σ置换成,并计算6,这一过程的计算结果 分布规律。 见表2。由表2的xn和,计算得到构造的极值1 《健筑结构荷载规范》虽然没有提供基本雪压 型概率分布的统计参数a和4,见表3。在计算a和 的相关参数,但提供了下列带有极值I型分布统计 时,样本容量按无穷大考虑。将a和u以及1/ 参数的雪压计算公式及相关参数计算公式
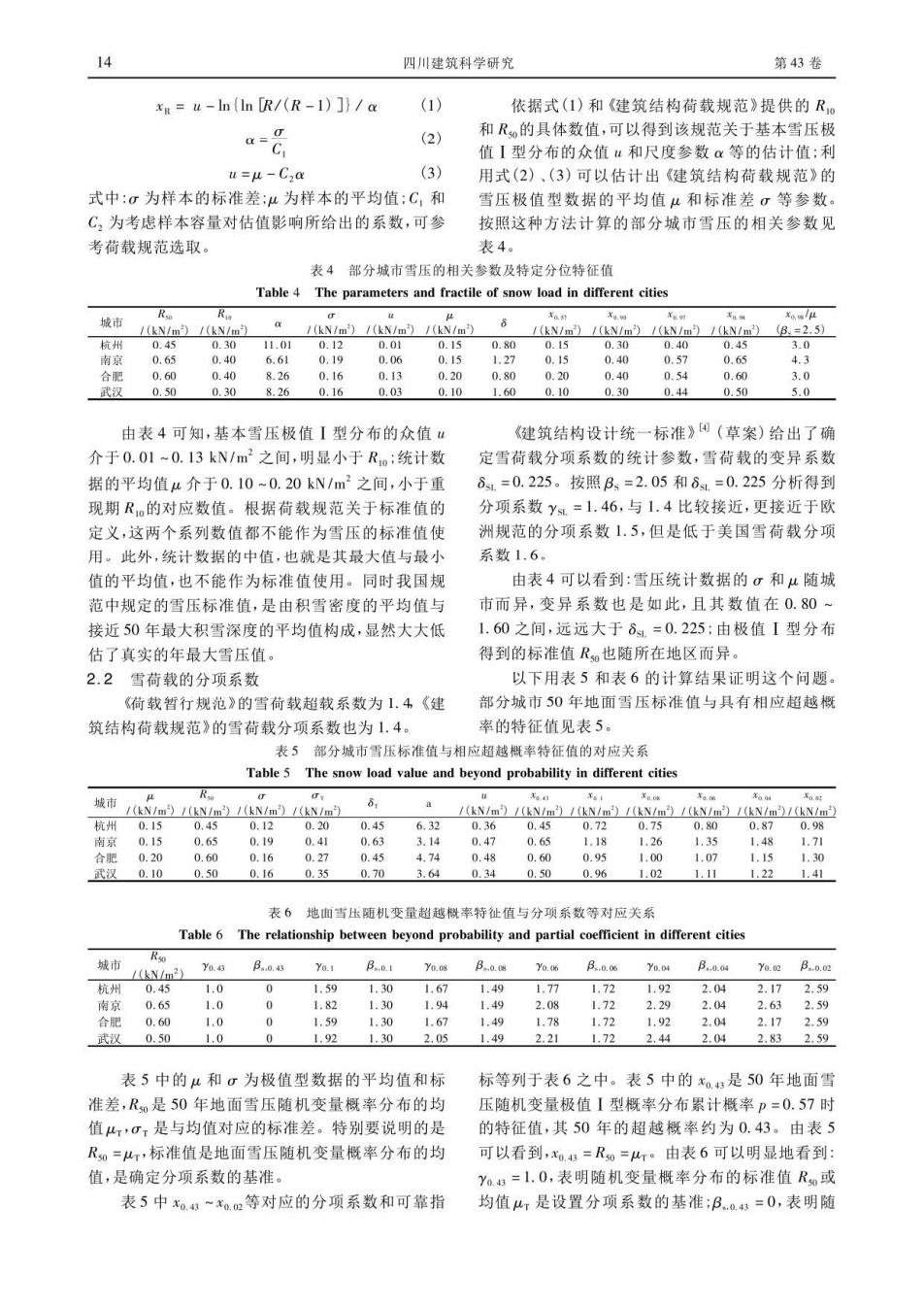
14 四川建筑科学研究 第43卷 xx=u-In(In [R/(R-1)]}/a (1) 依据式(1)和《律结构益载规范》提仕的 a= 和的具体数值,可以得到该规范关于 值型分布的众值 和尺度 数a等的估i u=u-Ca 用式(2)、(3)可以估计出《健筑结构荷载规范》的 式中:。为样本的标准差:4为样本的平均值:C,和 雪压极值型数据的平均值4和标准差σ等参数。 C,为考虑样本容量对估值影响所给出的系数,可参 按照这种方法计算的部分城市雪压的相关参数见 考荷载规范选取。 是4。 表4部分城市雪压的相关参数及特定分位特征值 Table 4 The p rs and fractile of snow load in different cities 域市 LN/m /(kN/m (kN (kN/m(k 0.6 010 0.15 0 0.10 0.8 0.16 0.30 由表4可知,基本雪压极值】型分布的众值心 《建筑结构设计统一标准》④(草案)给出了确 介于0.01-0.13kN/m2之间,明显小于R:统计数 定雪背载分项系数的统计参数,雪荷载的变异系数 据的平均值4介于0.10-0.20kN/m2之间,小于重 5,=0.225。按昭B。=2.05和6,=0.225分折得到 现期R的对应数值。根据荷载规范关于标准值 分项系数Y 与1.4比较接近,更接近于欧 定义,这两个系列数值都不能作为雪压的标准值使 洲规范的分项系数1.5,但是低于美国雪荷载分项 用。此外,统计数据的中值,也就是其最大值与最小 系数1.6 值的平均值,也不能作为标准值使用。同时我国规 由表4可以看到:雪压统计数据的σ和u随城 范中规定的雪压标准值,是由积雪密度的平均值与 市而异,弯异系数也是如此,日其数值在0.80 接近50年最大积雪深度的平均值构成,显然大大低 1.60之间,远远大于 =0.225:由极值1型分布 估了真实的年最大雪压值 得到的标准值R也随所在地区而异 2.2雪荷载的分项系数 以下用表5和表6的计算结果证明这个问题 《荷载暂行规范》的雪荷载超载系数为1.4《建 部分城市50年地面雪压标准值与具有相应超越杷 筑结构荷载规范》的雪荷载分项系数也为1.4 率的特征值见表5 部分城市雪压标准值与 应超越影率特 证值的对应关系 The snow load value and beyond pro 61 36 0.16 表6地血雪出随机变量超惑概率特祉值与分项系数等对应关杀 Table6 The relationship between beyond probability and partial coefficient in different cities 城市 Yo 4 B.Yo B. Yo.os B..o.o Yo.o4 B..Ye.t B..o. () 1.5 165 1.30 1.67 1.7 1.92 2.0 10 16 2.0 2.5 表5中的4和:为极值型数据的平均值和标 标等列于表6之中。表5中的x。,是50年地面雪 准差,R是50年地面雪压随机变量概率分布的均 压随机变量极值【型概率分布累计概率p=0.57时 值,,是与均值对应的标准差。 别要说明的无 的特征值,其50年的超 概奉约为 43 由表 R知=灯,标准值是地面雪压随机变量概率分布的均 可以看到,x。4:=Rn=灯。由表6可以明显地看到 值,是确定分项系数的基准。 Y。。=1.0,表明随机变量率分布的标准值R或 表5中n~m等对应的分项系数和可靠指 均值山,是设置分项系数的基准:Ba3=0,表明随

2017a.1 邸小坛,等:荷载标准值与分项系数的分析 15 机变量概率分布的标准值凡或均值4,是作用效应 确定标准值 可靠指标B.的起始点 3.2 楼面均布荷载的分项系数 表5中的。和x。u分别是50年地面雪压 《建筑结构设计统一标准》(草案)也给出了楼 机变量的极值1型概密分布累计概率D=0.98的特 而均布荷载的变异系数,持久的楼面可变荷载的变 征值和D=0.96的特征值对应的50年的超越概率 异系数8.,=0.229-0.292,临时的楼面可变荀载的 约为0.02和0.04。 变异系数6=0.322-0.36 。该标准(草案)使用 以上比较证明:当可靠指标或超越概率为统 临时性楼面可变荷载的统计数据需要推断50年 的数值时,各地的分项系数差异明显:或者说,无论 遇的楼面可变荷找标准值(当时尚没有重现期的根 何地都取同样的分项系数,各地雪压的可靠指标必 念)。因此,8,=0.322~0.369似可以暂时用于 然不同。也戴是说,使用同样的雪压分项系数,不符 算50年楼面均布益载的分项系数。依据移标相 合使用可靠指标方法的基 同时可以看出现 (草案)的解释,6」 =0.322可能适用于居住建筑和 行规范中的分项系数偏小 办公建筑,6 =0.369可能适用于公用建筑 3楼面均布荷载 按照自重荷载分项系数的分析方法,y,=1.4 和8.,=0.322=0.369对应的8=1.08-1.24,如 3.1楼面均布荷载的标准俏 果按B.=2.05和8.=0.322-0.369计算分折,v 关于楼面均布荷载的标准值,自然要从《健 =1.66-1.81,是1.4的1.2-1.3倍。 这里还要说 结构荷载规范)(G97 说起,前面曾提至 明的是,当楼面均布荷载可以用正态分布近似描述 《建筑结构荷载规范》仅对工业与民用建筑结构荷 时,也就是用标准值作为统计数据概率分布的均值 载规范》的商店和书库等的楼面标准荷载予以了调 时,B.=2.05对应于50年的超越概率为0.02 整,其他楼面均布荀载的标准值都与《工业与民用 4 建筑结构荷载规范》的标准荷载相同,而工业与民 结论 用建筑结构荷载规范》的标准荷载又与《荷载暂行 通过以上的分析,得出以下结论 规范》相同。从这比较似乎可以得到下列结论: 1)风荷载、雪荷载以及楼面均布荷载的标准值 )《荷载暂行规范》的楼面均布荷载标准值可 取值采用了使用平均值的方法,并不是真正的年最 能是引自国外的规范,并没有进行过实地的量测 大值,议使得最终的标准估信低 《工业与民用建筑结构荷载规范》只是将这些楼面 2)风荷载是基于风速分布所得出的,其分项系 均布荷载标准值称为30年 一遇最大值的平均值 数应乘以风速而不是风压 2)结构可靠度理论初创时确实进行过大量的 3)当可靠指标或超越概率为统一的数值时,各 调研和现场的实测实量,其统计方法可能是将一次 地的分项系数差异明显:或者说,无论何地都取同样 性现场空荆实量数据的平均值路加调整认定为10 的分项系数,各地风压和雪压的可靠指标必然不同。 年一遇的最大值,取多次调研最大值的平均值作为 也就是说,使用同样的雪压分项系数,不符合使用可 10年一遇的荷载值:以此为基准,推断了30年 靠指标方法的基本规则 或50年一遇最大值的平均值。 参考文献: 从以上分析情况来看,现行荷载规微楼面均布 描载标准值的基本内涵还是50年统计数据的平均 )荷段暂行规范:结规-1一58匀,北京:中国建筑工业出版社 并没有像《健筑结构设计统一标准》(草案)宜 称的,按极值1型分布的规则确定楼面可变荷载的 建筑构荷规范:G509一02.北家:中国建筑工业 出社,2012. 标准值,因为《工业与民用建筑结构荷我规范》和 ign loods for buildings and other ASCE 《荷载暂行规范》在确定标准荷载时,不可能按照极 值型数据的方式确定楼面可变荷找的特征值。木面 研究认为,楼面均布荷载的标准值是推断的50年 建筑结构设计统一标准:G6一4习,北京:中国建筑工业 出服社,194 大值的平均值,可近似视为50年楼面荷载随机变 概率分布的均值:由于其不符合极值型数据的基本 要求,因而不能按统计数据极值I型分布的分位值