
第4客第4潮石家庄铁道学院学报vol.4a.4 199112 JOURNAL OF SHIJIAZHUANG RAILWAY INSTITUTE Dee.1991 各种不定性对中心钢压杆极限承 载力的影响及抗力不定性分析 刘嘉武 (桥梁工程系) 【摘要】本文计算了某些影响因素不定性对中心钢压杆极限承载力的影响。对钢 压杆抗力不定性分析方法作了煤讨,指出了某些方法有不尽合理之处,对怎样更合理 地确定抗力不定性提出了建议。 【关健词】机限承载力;抗力不定性:初始缺陷:变异性 1概述 彩响压杆承载力的因素很多,如:材性、截面几何特性和各种初始缺陷等(本文只讨论这几 种因素的影响)。当它们取某些定值时,对压杆稳定极限承载力的影响已有不少的研究。然而, 这些因素都是随机变量,进而导致压杆抗力的随机性。因此,有必要研究各种因索的变异对压 杆抗力的影响。我们把影响因素i的变异性用X(X=i的实际值1的标准值)表示,称为i的不 定性。由于1的不定性引起抗力的变异用K表示,称为1的不定性对抗力的影响。而综合各 仲因素的变异所引起压杆抗力的变异性用K(K=抗力实际值/抗力标准值)表示,称为抗力 不定性。本文主要讨论当X为已知的情况下,如何计算K,进而确定K。 在压杆可靠度分析中有的将压杆抗力写成如下形式] R=Rx·Xx··Ke (1) 式中Rx一一抗力标准值(按规范算得的压杆抗力): X¥ 材料强度的不定性,等于材料强度的实际值与标准值之比: X、 截面几何特性的不定性,等于截面几何特性的实际值与标准值之比: K一一计算模式的不定性」 抗力不定性KR=Xy·XA·K 收精日期1991-05-30 ·33·

这种分析方法对压杆(稳定问题)来说是不尽合理的。因为压杆抗力(弯曲失稳极限承载 力)的变化一般并非随材料强度的变化而以相同的比例变化,而是随长细比的不同而不同。 截面的几何特性的不定性对抗力的影响也是如此,所以不能认为X=K。另外,各种缺陷,如初 弯曲、初偏心,残余应力等对抗力的乾响也是随长细比的不同而不同。如用计算模式的不定性 概括它们的影响也显得粗糙。所以有必要进一步研究上述各种因素对抗力的影响。由X,求K, 进而确定K。为此,将抗力的表达式写成如下形式: R=KR·R (2) 式中RK一一抗力标准值(各种不定性因素均取其标准值时算得的极限承截力): KR一一抗力不定性,用下式表示: K=K·K·KE·K·Ke·Kg·K 其中K一一计算模式的不定性: Kv、KA,K、K、K、Kg一一分别代表材料强度,截面尺寸、弹性模量,初曲矢度、荷载偏心 和残余应力的不定性对抗力的影响,等于相应的影响因素取实际值而其他因素均取标准值时 的计算极限承载力与抗力标准值之比。如材料强度的不定性对抗力的影响为 Kr=Ry/Rx 式中R,一材料强度(截面平均屈服应力)取实际值,而其他诸影响因素均取标准值时的极 限承载力。 首先,计算各种影响K、K、…,K,然后计算抗力不定性Kw,它们都是随机变量。 以下计算中是以铁路钢桁梁常用的H形截面绕弱轴失稳为例的。截面形式见图1,截面各 组成部分的尺寸比例为 Φ=H·T/(2H·T1+B·T2)=0.345 未考虑K的变异性影响。残余应力分布图形如图」 所示,取=0.35。 在计算抗力标准值Rx时,各种不定性因素取如下标 准值: 材料屈服强度的标准值f,=340MPa, 弹性模量的标准值Ex=210GPa: 截面几何特性按截面标准尺寸计: 杆件初曲矢度的标准值Dx=1/1000(1为杆长): 图1截面形式及残余应力 荷载初偏心的标准值Cx=0.008H(H为截面高): 残余应力的标准值nf,n=0.3。 现将“曲率分段法”计算压杆极限承载力的计算方法和结果介绍如下。 2材料强度的不定性对抗力的影响Ky 材料强度不定性用X,表示,X,=屈服强度的实际值/屈服强度的标准值。参照文献[3] 的统计数据取Xy的均值xY-1.0389,标准差o×v=0.0675,变异系数Vx=0.065(16Mn)。 根据不同的X,值分别算出不同长细比情况的下极限承载力凡,进而算出与各个X,对应 。34
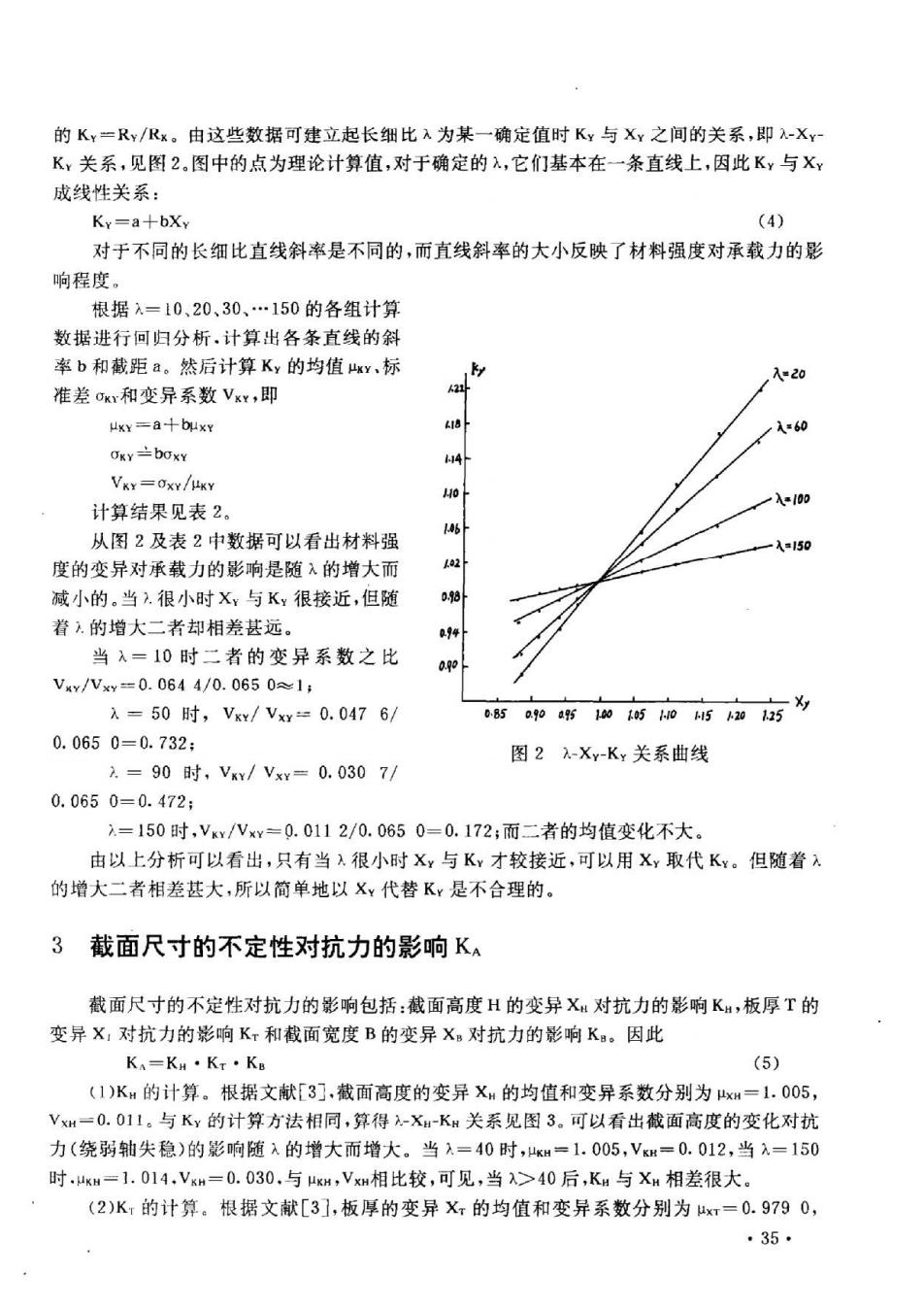
的Ky=Rv/Kx。由这些数据可建立起长细比入为某一确定值时Ky与X¥之间的关系,即-Xv K,关系,见图2图中的点为理论计算值,对于确定的入,它们基本在一条直线上,因此K,与X 成线性关系: Ky=a+bXy (4) 对于不同的长细比直线斜率是不同的,而直线斜率的大小反映了材料强度对承载力的影 响程度。 根据1=10,20、30、150的各组计算 数据进行何归分析,计算出各条直线的斜 率b和截距a。然后计算Ky的均值¥,标 20 准差w和变异系数VxY,即 uy=a+bux¥ 入60 Owy±b0xY VxY=0x/ 一入=00 计算结果见表2。 从图2及表2中数据可以看出材料强 -入=150 度的变异对承载力的影响是随入的增大而 减小的。当.很小时X¥与K¥很接近,但随 着入的增大二者却相差甚远。 94 当入=10时二者的变异系数之比 agob Vxv/Vxw=0.0644/0.0650≈1, x=50时,Vxx/Vxx=0.0476/ 脑如w烟场响5加西 0.0650=0.732: 图2λ-XyKy关系曲线 =90时,Vxx/Vx=0.0307/ 0.0650=0.472: 1=150时,Vkx/VxY=0.0112/0.0650=0.172;而二者的均值变化不大. 由以上分析可以看出,只有当人很小时Xy与K,才较接近,可以用X,取代K¥。但随着》 的增大二者相差甚大,所以简单地以X¥代替K:是不合理的。 3 截面尺寸的不定性对抗力的影响K 截面尺寸的不定性对抗力的影响包括:截面高度H的变异X对抗力的影响Ka,板厚T的 变异X,对抗力的影响K和截面宽度B的变异X,对抗力的影响K。因此 KA=KH·Kr·KB (5) (1)KH的计算。根据文献[3],截面高度的变异Xw的均值和变异系数分别为xw=1.005 Vxm=0.O11。与Ky的计算方法相同,算得X-KH关系见图3。可以看出截面高度的变化对抗 力(绕弱轴失稳)的影响随入的增大而增大。当入=40时,m=1.005,Vm=0.012,当入=150 时x=1.014.Vx4=0.030,与xm,Vxm相比较,可见,当>40后,KH与XH相差很大。 (2)K的计算。根据文献[3],板厚的变异X的均值和变异系数分别为x=0.9790, ·35·
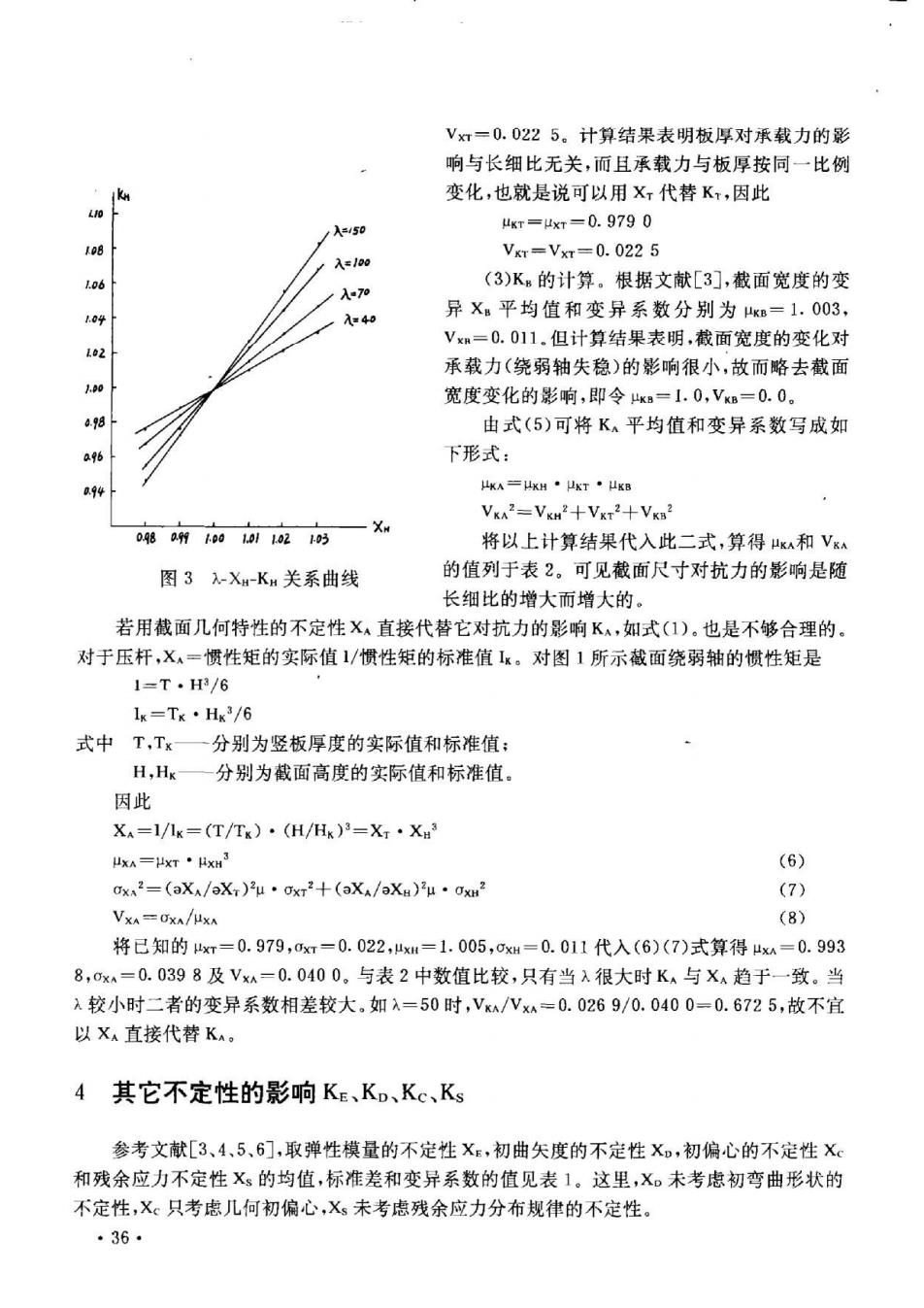
Vx灯=0.0225。计算结果表明板厚对承载力的影 响与长细比无关,而且承载力与板厚按同一比例 变化,也就是说可以用X,代替K,因此 uKr=ur=0.9790 /A=50 A=loo VxT=Vx灯=0.0225 A-70 (3)K的计算。根据文献[3],截面宽度的变 4 异X。平均值和变异系数分别为B=1.003, Vxm=0.011.但计算结果表明,截面宽度的变化对 承载力(绕弱轴失稳)的影响很小,故而略去截面 宽度变化的影响,即令w-1.0,Vk=0.0。 48 由式(5)可将K、平均值和变异系数写成如 % 下形式: =4H·k灯· VxA=VKH2+Vxt2+VKB2 将以上计算结果代入此二式,算得xA和Vx 图3XM-Km关系曲线 的值列于表2,可见截面尺寸对抗力的影响是随 长细比的增大而增大的。 若用截面几何特性的不定性X直接代替它对抗力的影响K,如式(1)。也是不够合理的, 对于压杆,X=惯性矩的实际值1/惯性矩的标准值k。对图1所示被面绕弱轴的惯性矩是 1=T.H/6 lk=Tx·Hw3/6 式中T,Tx一分别为竖板厚度的实际值和标准值: H,Hx 分别为截面高度的实际值和标准值, 因此 XA=1/1g=(T/Tg)·(H/Hk)3=Xx·X (6) oka2=(aX/oX)u·ox2+(oX/Xa)u·02 (7) VxA=Oxn/x (8) 将已知的x=0.979,0=0.022,=1.005,ox=0.011代入(6)(7)式算得=0.993 8,0xA=0.0398及Vx-0.0400。与表2中数值比较,只有当入很大时K与X趋于一致。当 较小时二者的变异系数相差较大.如=50时,V/Vx=0.0269/0.0400=0.6725,故不宜 以X直接代替K 4其它不定性的影响KE、Ko、Kc、Ks 参考文献[3、4、5、6],取弹性模量的不定性X:,初曲矢度的不定性X。,初偏心的不定性X 和残余应力不定性X的均值,标准差和变异系数的值见表1。这里,X。未考虑初弯曲形状的 不定性,X只考感儿何初偏心,X未考感残余应力分布规律的不定性。 .36
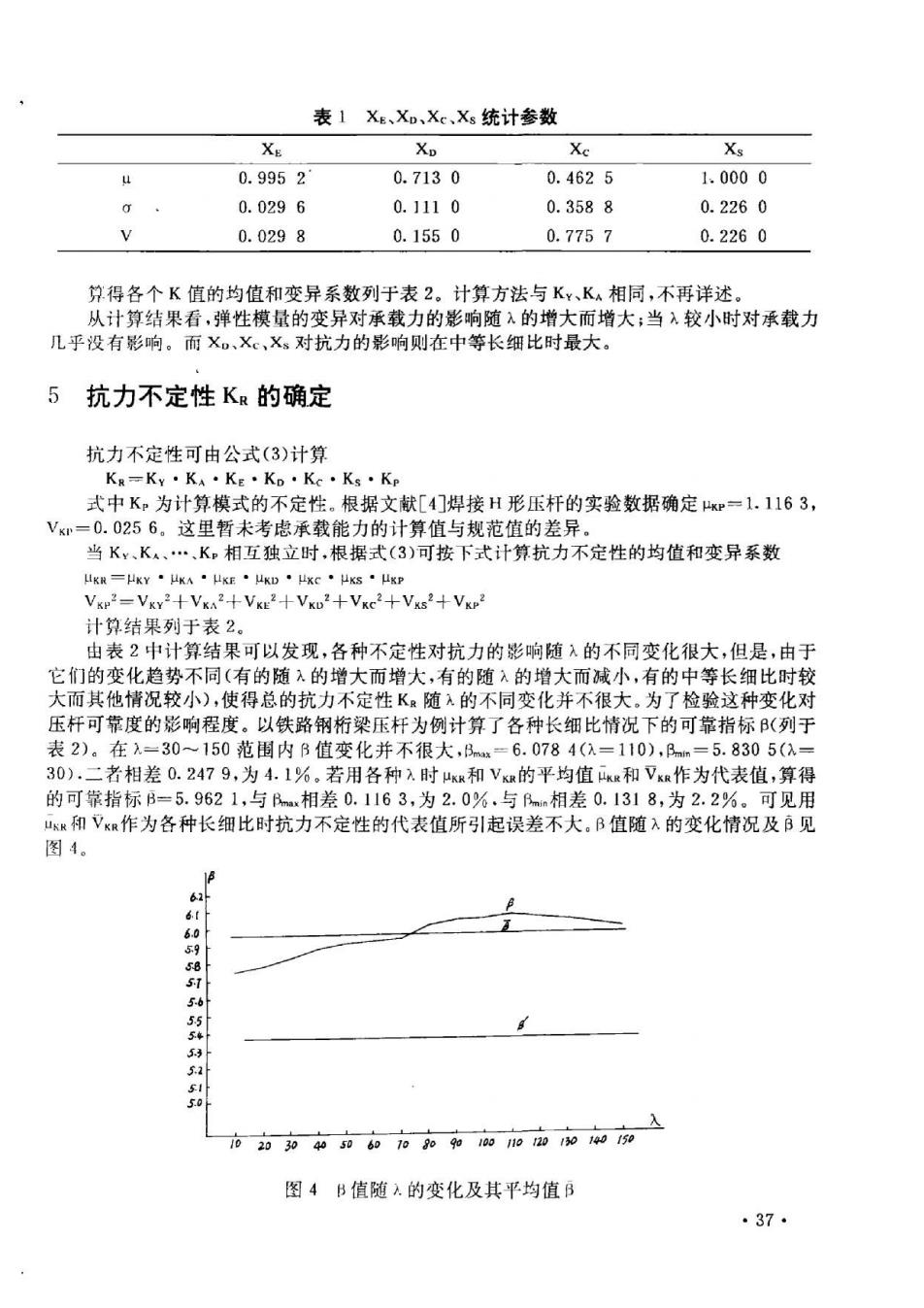
表1X、X知,Xc,Xs统计参数 XE X X X 0.9952 0.7130 0.4625 1.0000 0.0296 0.1110 0.3588 0.2260 0.0298 0.1550 0.7757 0.2260 算得各个K值的均值和变异系数列于表2。计算方法与K、K相同,不再详述。 从计算结果看,弹性模量的变异对系载力的影响随入 增大而增大当入较小时对承载力 几乎没有影响。而X,X,Xs对抗力的影响则在中等长细比时最大。 5抗力不定性K的确定 抗力不定性可由公式(3)计算 KR=Ky·Ka·KE·KD·Ke·Ks·Ke 式中K。为计算模式的不定性。根据文献[4门焊接H形压杆的实验数据确定=1.1163, V=0.0256。这里暂未考虑承载能力的计算 直与规范值的差异 当KK….K。相互独立时,根据式(3)可按下式计算抗力不定性的均值和变异系数 g一k¥·gA·μxE·μKD·xC·μs·gP VxP2=VxY:+VKa2+VKE2+VKD2+Vxc2+Vx52+Vx 计算结果列于表2。 由表2中计算结果可以发现,各种不定性对抗力的影响随入的不同变化很大,但是,由于 它们的变化趋势不同(有的随入的增大而增大,有的随入的增大而减小,有的中等长细比时较 大而其他情况较小),使得总的抗力不定性K.随入的不同变化并不很大。为了检验这种变化对 压杆可靠度的影响程度。以铁路钢析梁压杆为例计算了各种长细比情况下的可靠指标B(列于 表2) 在=30一150范围内B值变化并不很大, 6.0784(=110),B 5.83051 30). 者相差0.2479,为4.1%,若用各种入时和Vu的平均值u和V作为代表值,算得 的可常指标B-5.9621,与相差0.1163,为2.0%.与Bn相差0.1318,为2.2%。可见用 R和Vx作为各种长细比时抗力不定性的代表值所引起误差不大。B值随入的变化情况及百见 图4。 市西动如的如0前物加加西加加肉入 图4B值随人的变化及其平均值B ·37

表2各种不定性影响、抗力不定性及B值 A n s k VE Vr Vis VER 9 10 1.03861.0000.98241.00081.01131.00001.1528 0.0644 0.00000.02370.00030.00760.00070.0736 5.7461 20 1.0370 1.000 0.9826 1.0021 1.0136 1.0000 1.1561 5.7803 0.06260.00000.02400.00110.00920.00330.0724 1.03590.999 0.9833 1.00581.01681.00001.1628 0.06020.00010.0244 0.00210.61120.00860.07126 5.8305 40 1.0313 099g 0.9838 1.0084 1.0194 1.0000 1.163 5.8851 0.05280.00540.02550.00330.0f320.0169 0.0678 % 1.02820.999 0.98461.01261.02441.0000 1.1710 5.9070 0.04760.0063 0.02690.00470.01590.02770.0688 60 1.0281 0.999 0.9854 1.0187 .0325 1.0000 1.1883 5.9341 0.0433 0.0079 0.027】 0.0070 0.0216 0.038 0.0728 1.0255 0.998 0.9861-L.0247 1.0374 1.0000 1.1988 70 5.9428 0.04320.0101 0.0283 0.00920.0247 0.0M00 00756 80 1.021 0.998 0.9874 1.0302 1.041 1.0000 1.2051 0.0360 0.0128 0.0110 6.0216 0.0299 0.0255 0.0383 0.0724 90 1.0180 0.997 0.9887 1.0335 1.0364 1.0000 1.1999 6.0483 0.03070.0157 0.0318 0.0122 0.0240 0.0341 0.0689 1.1928 100 1.01440.997 0.98971.0336 1.03281.0000 00247 0018 0.03341 0.0125 0.0217 0.0655 6.0622 0.030 1.0121 0.997 0.9910 1.0340 1.0287 1.0000 1.1874 110 6.0784 0.02080.02050.0345 0.0123 0.0187 0.0262 0.0624 1.00960.996 0.99161.0324 102A1 1.00001.1768 120 0.0165 0.0219 0.0355 0.0118 0.0160 0.0226 0.0598 6.0600 130 1.00880.996 0.9922 1.0309 1.0209 1.0000 1.171 6.0490 0.01470.02300.0362 0.0113 0.0139 0.0196 0.0585 1.00680.99660.99261.02971.01801.00001.1646 0.0121 0.0238 0.0371 0.0107 0.0118 0.0172 0.0574 6.0288 150 1.00670.996 0.9929 1.0276 1.0156 1.0000 .1598 6.0116 0.01120.02470.03730.01010.01030.01530.0568 6结语 通过以上计算分析可以看出: (「)各种不定性对抗力的影响一船随长细出不同而不同,阳综合客种影响之后的抗力不 定性随长细比不同变化不很大,可用平均值或某一适当值作为各种长细比时的代表值。 (2)各种影响因素的变异与其引起的抗力变异是不相同的。因此,应以各种不定性对抗 力的实际彩响为依据来确定抗力的不定性。 另外,本文还存在许多不足,有待进一步改进。 38·

(1)对各种影响因素的考虑还不够全面,许多参数的取值比较粗糙,甚至根据不足,好 在本文的目的是探讨合理的分析方法,所以对所得结论不会有很大影响。 (2)本文所考虑的各种不定性X是相互独立的,但它们对抗力的影响K却不是相互独立 的。本文尚未全面考虑它们相互间的影响。 参考文献 1夏正中,陈国兴.钢轴压杆柱子曲线的建议及其可靠度分析.重庆建筑工程学院学报, 1984,(2):1~15 2刘嘉武.曲率分段法计算钢压杆单轴失稳极限承载力.石家庄铁道学院学报,1990, (1):1~8 3陈国兴,李继华.钢构件材料强度及其截面几何特性的统计参数.重庆建筑工程学院 学报,1985,(1):1~23 4潘际炎主编.栓焊钢桥的研究.北京:中国铁道出版社,1983.274~295 5钱冬生.钢压杆的承载力.北京:中国铁道出版社,1980,206~208 6 G.Ballio,F.M.Mazzolani.Theory and Design of Steel Structures.Chapman and Hall, 1983,111-134 Effect of Certain Indeterminateness on Ultimate Loads of Centrally -loaded Steel Columns and Analysis of Resistance Indeterminateness Liu Jiawu (Department of Bridge Engineering) [Abstract]The effect of certain indeterminateness on the ultimate loads of centrally-loaded columns is calculated in this paper,and the method of analyzing resistance indeterminateness discussed. Comments on some methods that are unreasonable are made and some ideas for the reasonable determination of resistance indeterminateness suggested. [Keywords]ultimate bearing resistance;resistanee indeterminateness;initial imperfection; variability ·39·